
- •1. Короткий опис
- •2. Вказівки до виконання роботи
- •3. Зміст роботи
- •4. Порядок виконання роботи
- •6. Питання для контролю
- •1. Короткий опис
- •2. Зміст роботи
- •3. Запис математичної моделі ланки другого порядку
- •4. Порядок виконання роботи
- •6. Питання для контролю
- •1. Короткий опис
- •2. Зміст роботи
- •3. Запис математичної моделі коливальної ланки
- •4. Порядок виконання роботи
- •6. Питання для контролю
- •1. Короткий опис.
- •3. Порядок виконання роботи
- •5. Питання для контролю
- •1.Математична модель системи
- •2. Зміст роботи
- •3. Порядок виконання роботи.
- •5. Питання для контролю.
- •2.Зміст роботи
- •3.Порядок виконання роботи:
- •5.Питання для самоконтролю
- •1.Структурна схема та математична модель сар.
- •2. Вихідні дані для виконання лабораторної роботи
- •3. Порядок виконання роботи
- •Запитання для самоконтролю
- •3.Порядок виконання роботи
- •Питання для самоконтролю
- •Використана література
- •Дубравін Юрій Федорович Теорія систем автоматичного управління
- •03049, Київ – 49, вул. Миколи Лукашевича, 19
2. Вихідні дані для виконання лабораторної роботи
Вихідні дані для виконання лабораторної роботи приведені в таблиці 1.
Таблиця 1. Параметри САР
-
Параметри ланок
Робочі місця
1
2
3
4
5
6
7
8
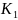
2
1,5
2,5
2,8
3
3,2
3,4
3,6

6
6,5
5
4,8
5
4,6
4,8
5
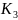
3
3
2
2,1
2,2
2,4
2,8
1,8
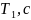
90
85
80
75
70
65
60
55
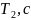
3
3,5
4
4,5
5
5,5
6
7
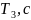
20
18
16
14
22
24
26
25
3. Порядок виконання роботи
Параметри ланок для виконання роботи задаються викладачем.
Після запуску Mathcad необхідно:
ввести вихідні дані ланок;
задати інтервал зміни частоти в межах 0-100 1/с з кроком 0.05;
присвоїти
значення уявній одиниці
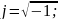
виконати розрахунок:
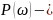 дійсної
частини КПФ;
дійсної
частини КПФ;
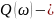 уявної
частини КПФ;
уявної
частини КПФ;
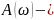 модуля
КПФ;
модуля
КПФ;
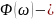 аргумента
КПФ;
аргумента
КПФ;
Розрахувати значення ЛАЧХ. Визначити точки перетину годографа АФЧХ з дійсною та уявною осями.
4.Зміст звіту
Структурна схема ланки, передавальні функції ланок та розімкнутої САР;
КПФ розімкнутої САР;
таблиці
значень
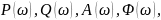 знайдені для двох варіантів;
знайдені для двох варіантів;
годограф АФЧХ;
графіки ЛАЧХ та ЛФЧХ, побудовані на одному рисунку.
Вказати наявність та значення запасів по фазі та амплітуді та значення частот, при яких годограф перетинає дійсну та уявну осі.
Запитання для самоконтролю
1. Як визначити стійкість за допомогою ЛАЧХ та ЛФЧХ? 2. Як визначити значення коефіцієнта передачі системи за допомогою годографа АФЧХ?
3.
Як визначити частоту, при якій годограф
АФЧХ перетинає уявну вісь
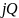 ?
?
Лабораторна робота № 8. Аналіз якості системи автоматичного управління
Мета роботи: визначення перехідної та усталеної складових похибки регулювання, побудова перехідної функції.
Передавальна функція САУ за похибкою. Визначення похибки регулювання.
Показники
якості системи, структурна схема якої
приведена на рис.1 в перехідному і
усталеному режимах можна оцінювати не
тільки за характером зміни вихідної
величини, а і за зміною похибки


Рис.1. Структурна схема замкнутої САУ
При
одиничному вхідному впливі

 (1)
(1)
Аналіз
похибки дає відповідь про точність
системи в перехідному та усталеному
режимах.При цьому можна побудувати
перехідну функцію за формулою:
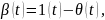
або
 .
(2)
.
(2)
Для
визначення похибки
 використаємо метод розкладу зображення
похибки системи на елементарні дроби.
Передавальна функція системи за похибкою
відносно впливу з одиничним зворотним
зв’язком
використаємо метод розкладу зображення
похибки системи на елементарні дроби.
Передавальна функція системи за похибкою
відносно впливу з одиничним зворотним
зв’язком
 ,
(3)
,
(3)
де
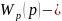 передавальна
функція розімкнутої системи.
передавальна
функція розімкнутої системи.
З
виразу (3) зображення похибки: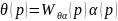 .
.
Передавальні функції ланок системи:
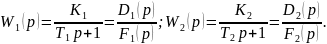
Передавальна функція системи в розімкнутому стані:
 (5)
(5)
Передавальна функція системи за похибкою згідно (3):
 ,
(6)
,
(6)
де .
Так
при підстановці першого кореня
 отримаємо
отримаємо
 ,
модуль
,
модуль
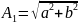 ,
аргумент
,
аргумент
 .
.
Перехідна
складова похибки при одній парі
комплексно-спряжених коренів та одному
дійсному корені характеристичного
рівняння визначається за формулою:
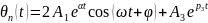 .
(7)
.
(7)
Початкове
значення компоненти, що відповідає
комплексно-спряженим кореням визначається
виразом при
 рівним
рівним
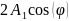 .
.
Початкове
значення компоненти
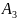 ,
що відповідає дійсному кореню
,
що відповідає дійсному кореню
 отримаємо при підстановці у вираз (7)
значення цього кореня. При правильно
обчислених початкових значеннях їх
сума
отримаємо при підстановці у вираз (7)
значення цього кореня. При правильно
обчислених початкових значеннях їх
сума
 .
.
Перехідна складова похибки системи:
(8)
так
як вимушена складова помилки
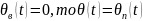
Перехідна
функція
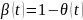
2.Вихідні дані до виконання лабораторної роботи приведені в таблиці 1.
Таблиця 1. Параметри ланок САР
Параметри ланок |
Робочі місця |
|||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0,1 |
1 |
2,5 |
0,2 |
2 |
2,8 |
35 |
3 |
|
20 |
20 |
5 |
30 |
18 |
4,5 |
0,3 |
24 |
|
0,1 |
0,001 |
0,02 |
0,2 |
0,002 |
0,03 |
0,4 |
0,003 |
|
0,2 |
0,083 |
0,09 |
0,3 |
0,009 |
0,08 |
0,25 |
0,01 |
Вводимо позначення:

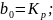
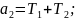
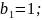
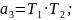
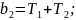
Тоді передавальна функція системи за похибкою прийме вид:
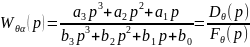 (4)
(4)
Характеристичне рівняння системи:
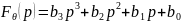
При
рішенні рівняння визначаємо корені
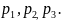
Похибка системи складається з двох складових:
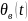 –
вимушеної
складової спричиненої задавальним
діянням;
–
вимушеної
складової спричиненої задавальним
діянням;
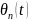 -
перехідної складової спричиненої зміною
-
перехідної складової спричиненої зміною
 ,
при цьому
,
при цьому
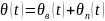 (5)
(5)
В залежності від значення коренів характеристичного рівняння можливі два варіанти рішення.
Варіант 1: Корені характеристичного рівняння системи дійсні і від’ємні.
Перехідна
складова похибки:
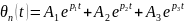 (6)
(6)
де початкові значення її складової перехідної помилки:
 (7)
(7)
При
підстановці у вираз (7) значень коефіцієнта
коренів
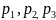 отримаємо значення початкових складових
отримаємо значення початкових складових
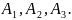
При
відсутності помилок в обчисленні:

Записуємо
згідно (6) вираз
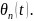 При
вхідному впливі типу одиничного скачка
При
вхідному впливі типу одиничного скачка
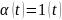 вимушена складова
вимушена складова
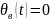 і тому
і тому
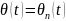 .
.
Варіант
2:
Серед коренів характеристичного рівняння
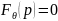 є комплексно-спряжені корені
є комплексно-спряжені корені
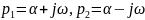 ,
то при їх підстановці до виразу (7) для
,
то при їх підстановці до виразу (7) для
 отримаємо
комплексні числа.
отримаємо
комплексні числа.
