Контрольні питання до теми 1

1. Нехай a  А. чи Потрібно звідси, що {a} А?

2. У якому випадку А АВ?

3. Назвіть множину, що є підмножиною будь-якої множини.

4. Чи може бути множина еквівалентна своїй підмножині?

5. Потужність якої множини більша: множини натуральних чисел або множини точок відрізка [0, 1]?

Задачі для самостійного розв’язування

Задача 1

1. Чи справедливо в загальному випадку твердження: якщо А B, B С і С D, то A D?

2. Чи може при деяких А, В, С і D виконатися набір умов: А B, B С, С D і A D?

Таблиця 1.6

Задача 2

Для універсальної множини U = {-5, -4, -3, -2, -1,1,2,3,4,5}, множини А , заданої списком, і для В, множина коренів рівняння є:

+ + + + =0.

1. Знайти множини:

.

2. Знайти і .

Таблиця 1.7

Задача 3

Нехай А, В і С - множини точок площини, координати яких задовольняють умовам відповідно. Зобразіть у системі координат х0у множину D, отриману з множин А, В і С за формулою .

Таблиця 1.8

Таблиця 3(продовження)

Таблиця 3(продовження)

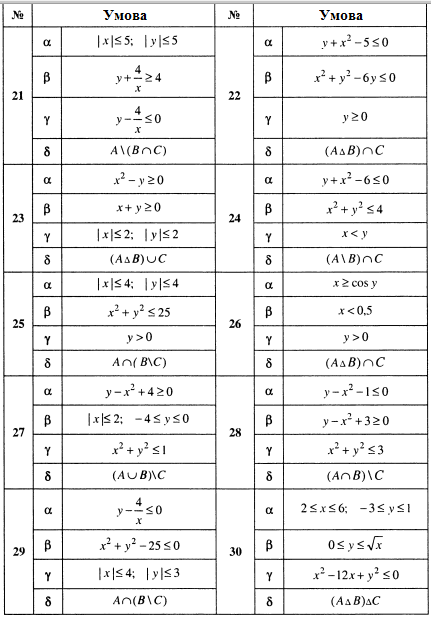
Задача 4

1. Чи існують множини А, В, X такі, що виконується набір умов ?

2. Чи існують множини N, Е, Р такі, що виконується набір умов ?

Таблиця 1.9

Таблиця 1.9(продовження)

Задача 5

З'ясувати взаємне розташування множин D, Е, F, якщо А, В, X - довільні підмножини універсальної множини U.

Таблиця 1.10

Таблиця 1.10 (продовження)

Таблиця 1.10 (продовження)

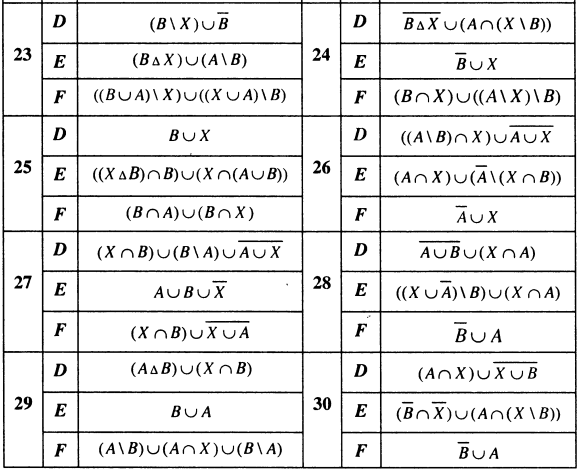
Задача 6

Перевірити, що для будь-яких множин А, В, С виконання включення зумовлює виконання включення .

Таблиця 1.11

Таблиця 1.11 (продовження)

Задача 7

Для довільних множин А, В, Н перевірити, чи є виконання включення необхідною і достатньою умовою для виконання рівності .

Таблиця 1.12

Задача 8

Розв’язати систему співвідношень відносно множини X і вказати умови сумісності системи.

Таблиця 1.13

Задача 9

1. Перевірити справедливість рівності для множин

А = {1,2}, В = {2,3}, С = {1,3}.

2. З'ясувати, чи вірно рівність для довільних А, В, С.

Таблиця 1.14

Таблиця 1.14(продовження)

Задача 10. Які з наведених нижче виразів є невірними і чому:

Задача 11. Записати множину коренів рівняння x²+x-12=0.

Задача 12. Записати множину прямих площини, паралельних прямій y=2x+3.

Задача 13. Що можна сказати про множину А={a,b}, якщо:

а) a, b – найменші двоцифрові натуральні, що діляться на 3 і 4 відповідно;

б) a, b – найбільші двоцифрові числа, що діляться на 3 і 4 відповідно?

Задача 14. Чи є рівними множини А і В?

1. А={1, 2, {1, 2}, 3}, B={3, 2, 1};

2. A={a, b, x} i B={(a, b), x}.

Задача 15. У яких відношеннях (, , , , , , ) перебувають між собою множини А, В, С і D:

А={1, 3}, B={x | x – непарне число}, С={x | x²-4x+3=0}, D={1, 2, 3, 4, 5} ?

Задача 16. Нехай А={1, 2, 3, 4, 5, 6}, B={1, 3, 5, 7, 9}. Знайти AB, AB, A\B, AB.

Задача 17. Що є доповненням до множини А у множині В:

1. А={a, c, e}, B={a, b, c, d, e, f};

2. A=(- ; 2][4; 6), B=(- , 10];

3. A=N, B=Z₊?

Задача 18. Записати буліан множини М ((М)), якщо М=((АВ)С)(А\С), А={a, b, c, d, e, g}, В={d, e, f, g}, C={c}.

Задача 19. Довести теорему де Моргана:

1) ;

2) (домашнє завдання).

Задача 20. Спростити вираз: .