1.2. Операції над множинами

Розглянемо основні операції над множинами.

Об'єднанням множин А и В називається множина АВ, всі елементи якого є елементами хоча б одного із множин А або В:

АВ = {x  x А або xВ}.

З визначення слідує, що А  АU і В  АВ.

Аналогічно визначається об'єднання декількох множин

Приклад 1.8.

а) Нехай А = {4, 5, 6}, В = {2, 4, 6}.

Тоді АВ = {2, 4, 5, 6}.

б) Нехай А – множина чисел, які діляться на 2, а В – множину чисел, які діляться на 3:

А = {2, 4, 6, …}, В = {3, 6, 9, …}...

Тоді А В множину чисел, які діляться на 2 або на 3:

АВ = {2, 3, 4, 6, 8, 9, 10, …}...

Перетинум множин А и В називається множина АВ, всі елементи якого є елементами обох множин А и В:

АВ = {x  x А и xВ}.

З визначення слідує, що АВ  А, АВ  U і АВ  АВ.

Аналогічно визначається перетин декількох множин.

Приклад 1.9.

Розглянемо дані із приклада 1.8.

а) Нехай А = {4, 5, 6}, В = {2, 4, 6}.

Тоді АВ = {4, 6}.

б) Нехай А – множина чисел, які діляться на 2, а В – множину чисел, які діляться на 3:

А = {2, 4, 6, …}, В = {3, 6, 9, …}...

Тоді АU множину чисел, які діляться й на 2 і на 3:

АВ = {6, 12, 18, …}...

Може виявитися, що множини не мають жодного спільного елемента. Тоді говорять, що множини не перетинаються, або що їхній перетин - порожня множина.

Приклад 1.10.

Нехай А = {1, 2}, В = {2, 3}, C = {3, 4}.

Тоді АВC =.

Відносним доповненням множини В до множини А називається множина А \ В, всі елементи якого є елементами множини А, але не є елементами множини В:

А \ В = {x  x А и xВ}.

Приклад 1.11.

Розглянемо дані із приклада 1.8.

а) А = {4, 5, 6}, В = {2, 4, 6}.

А \ В = {4, 5}, В \ А= {2}.

б) А = {2, 4, 6, …}, В = {3, 6, 9, …}...

Тоді А \ В – множину чисел, які діляться на 2, але не діляться на 3, а В \ А – множину чисел, які діляться на 3, але не діляться на 2:

А \ В = {2, 4, 8, 10, 14, …}...

В \ А= {3, 9, 15, 21, 27, …}...

Симетричною різницею множин А и В називається множина А + В:

А + В = (А \ В)  (В \ А).

Приклад 1.12.

Розглянемо дані із приклада 1.11.

а) А = {4, 5, 6}, В = {2, 4, 6}.

А \ В = {4, 5}, В \ А= {2}, А + В = {2, 4, 5}.

б) А = {2, 4, 6, …}, В = {3, 6, 9, …}, А \ В = {2, 4, 8, 10, 14, …}...

В \ А= {3, 9, 15, 21, 27, …}, А + В = {2, 3, 4, 8, 9, …}...

Універсальною множиною називається така множина U, що всі розглянуті в даній задачі множини є його підмножинами.

Абсолютним доповненням множини А називається множина всіх таких елементів x  U, які не належать множині А: = U \ A.

Приклад 1.13.

Нехай А – множина позитивних парних чисел.

Тоді U – множина всіх натуральних чисел й - множина позитивних непарних чисел.

1.3. Геометричне моделювання множин. Діаграми Венна

Для наочного подання множин і відношень між ними використається діаграми Венна (іноді їх називають кругами Ейлера або діаграмами Ейлера - Венна).

Універсальну множину зображують у вигляді прямокутника, а множини, що входять в універсальну множину, - у вигляді кіл усередині прямокутника; елементу множини відповідає точка усередині кола (рис 1.1а)).

За допомогою діаграм Венна зручно ілюструвати операції над множинами.

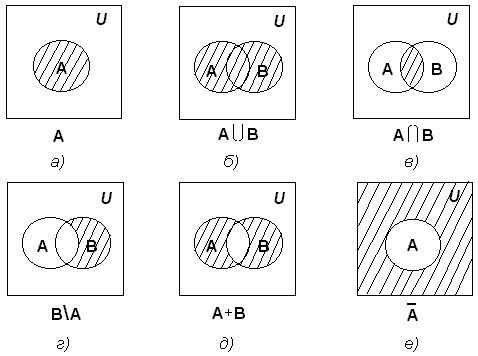
Рис.1.1