3.10. Дерева. Основні визначення

Неорієнтованим деревом (або просто деревом) називається зв'язний граф без циклів. Цьому визначенню еквівалентні, як легко показати, що випливають визначення:

а) дерево є зв'язний граф, що містить n вершин й n - 1 ребер;

б) дерево є граф, будь-які дві вершини якого можна з'єднати простим ланцюгом.

Приклад 3.17.

Графи, зображені на рис. 3.12, є деревами.

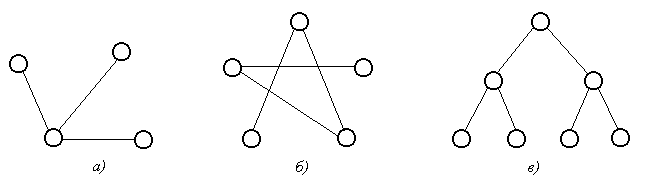
Рис. 3.12

Якщо граф незв'язний і не має циклів, то кожний його зв'язний компонент буде деревом. Такий граф називається лісом. Можна інтерпретувати рис. 6.1 як ліс, що складається із трьох дерев.

Остовним деревом зв'язного графа G називається будь-який його підграф, що містить всі вершини графа G і є деревом.

Приклад 3.18.

Для графа, зображеного на рис. 3.13а), графи на рис. 3.13б) і 3.13в) є остовними деревами.

Рис. 3.13

Нехай граф G має n вершин й m ребер Тому, що всяке дерево з n вершинами по визначенню (див. розділ 6.1) має n – 1 ребер, те будь-яке остовное дерево графа G виходить із цього графа в результаті видалення m – (n – 1) = m – n + 1 ребер. Число g = m – n + 1 називається цикломатичним числом графа.

3.11. Мінімальні остовні дерева зважених графів

Граф G = (X, A) називається навантаженим, якщо для кожного ребра (x_i,x_j) визначена його довжина (або вага) c_ij.

Нехай G - зв'язний навантажений граф. Задача побудови мінімального остовного дерева полягає в тому, щоб із множини остовних дерев знайти дерево, у якого сума довжин ребер мінімальна.

Приведемо типові випадки, коли виникає необхідність побудови мінімального остовного дерева графа.

а) Потрібно з'єднати n міст залізничними лініями (автомобільними дорогами, лініями електропередач, мережею трубопроводів і т.д.) так, щоб сумарна довжина ліній або вартість була б мінімальною.

б)Потрібно побудувати схему електричної мережі, у якій клеми повинні бути з'єднані за допомогою проводів найменшої загальної довжини.

Задачу побудови мінімального остовного дерева можна вирішити за допомогою наступного алгоритму.

Алгоритм 3.2 (Алгоритм Краскала).

Крок 1. Установка початкових значень.

Уводиться матриця довжин ребер C графа G.

Крок 2. Вибрати в графі G ребро мінімальної довжини. Побудувати граф G₂, що складається з даного ребра й инцидентных йому вершин. Покласти i = 2.

Крок 3. Якщо i = n, де n - число ребер графа, то закінчити роботу (задача вирішена), у противному випадку перейти до кроку 4.

Крок 4. Побудувати граф G_{i +1,} додаючи до графа G_i нове ребро мінімальної довжини, обране серед всіх ребер графа G, кожне з яких інцидентне якій-небудь вершині графа G_i й одночасно інцидентне якій-небудь вершині графа G, що не належить в G_i. Разом із цим ребром включаємо в G_{i +1} і інцидентну йому вершину, що не включається в G_i. Привласнюємо i:= i +1 і переходимо до кроку 3.

Приклад 3.19.

Знайдемо мінімальне остовное дерево для графа, зображеного на рис. 3.14.

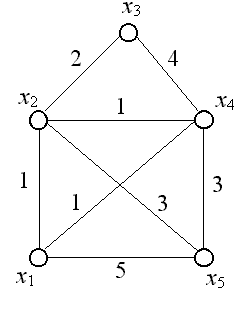
Рис. 3.14

Крок 1. Установка початкових значень.

Уведемо матрицю довжин ребер C:

С = .

Крок 2. Виберемо ребро мінімальної довжини. Мінімальна довжина ребра дорівнює одиниці. Таких ребер три: (x₁, x₂), (x₁, x₄), (x₂, x₄). У цьому випадку можна взяти кожне. Візьмемо (x₁, x₂). Побудуємо граф G₂, що складається з даного ребра і інцидентних йому вершин x₁ та x₂. Покладемо i = 2.

Крок 3. Тому, що n = 5, то i ¹ n, то переходимо до кроку 4.

Крок 4. Будуємо граф G_3, додаючи до графа G₂ нове ребро мінімальної довжини, обране серед всіх ребер графа G, кожне з яких інцидентне однієї з вершин x₁, x₂ і одночасно інцидентне якій-небудь вершині графа G, що не належить в G₂ т. е. однієї з вершин x₃, x₄, x₅. Таким чином, потрібно вибрати ребро мінімальної довжини з ребер (x₁, x₄), (x₁, x₅), (x₂, x₃), (x₂, x₄), (x₂, x₅). Таких ребер довжини одиниця два: (x₁, x₄) і (x₂, x₄). Можна вибрати кожне. Візьмемо (x₁, x₄). Разом із цим ребром включаємо в G₃ вершину x₄, що не належить в G₂. Думаємо i = 3 і переходимо до кроку 3.

Крок 3. Тому що i ¹ n, тому переходимо до кроку 4.

Крок 4. Будуємо граф G_4, додаючи до графа G₃ нове ребро мінімальної довжини з ребер (x₁, x₅), (x₂, x₃), (x₂, x₅), (x₄, x₅). Таке ребро довжини два одне: (x₂, x₃). Разом із цим ребром включаємо в G₄ вершину x₃, що не належить в G₃. Думаємо i = 4 і переходимо до кроку 3.

Крок 3. Тому що i ¹ n, тому переходимо до кроку 4.

Крок 4. Будуємо граф G_5, додаючи до графа G₃ нове ребро мінімальної довжини з ребер (x₁, x₅), (x₂, x₅), (x₄, x₅). Таких ребер довжини три два: (x₂, x₅) і (x₄, x₅). Візьмемо (x₂, x₅). Разом із цим ребром включаємо в G₅ вершину x₅, що не належить в G₄. Думаємо i = 5 і переходимо до кроку 3.

Крок 3. Тому що i = n, те граф G₅ – шукане мінімальне остовное дерево. Сумарна довжина ребер дорівнює 1 + 1 + 2 + 3 = 7.

Процес побудови мінімального остовного дерева зображений на рис. 3.15.

Рис. 3.15

Приклад 3.20

Неорієнтований граф мультиграф на 9 вершинах заданий вектором Rmn (табл. 9.13), де m та n – номера вершин графа. Неорієнтований граф заданий вектором Rmn (табл. 1), де m та n – номера вершин графа, m= 9,1 та n= 9,1 . Елементи вектора Rmn відповідають кількості ребер між відповідними вершинами m та n.

Таблиця 1.

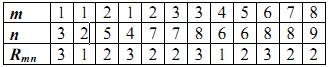
Для заданого графа необхідно:

 побудувати матрицю суміжності, діаграму графа;

 знайти у графi ейлерів та (або) гамiльтонів цикли, якщо вони є;

 визначити числові характеристики графа: хроматичне число, реберне

хроматичне число, цикломатичне число;

 побудувати деяке остовне дерево графа;

 записати код остовного дерева;

 побудувати базис розрiзiв графа, базис циклів графа.

Запишемо матрицю суміжності (табл. 2).

Таблиця 2.

З матрицi сумiжностi видно, що граф матиме 26 ребер і 9 вершин. З таблицi можна побудувати діаграму графа та його матрицю iнциденцiї.

Гамiльтонів цикл відсутній, оскільки граф має точку счленення V8. Число компонент зв’язності – 1.

Визначимо степені усіх вершин. deg v₁=7; deg v₂=5; deg v₃=8; deg v₄=4; deg v₅=4; deg v₆=6; deg v₇=6; deg v₈=10; deg v₉=2.

Заданий граф має 2 вершини з непарним степенем. Враховуючи достатні умови існування ейлеревих ланцюгів, у заданому графі присутній ланцюг. Знайдемо даний ланцюг, використовуючи алгоритм Фльорі.

Обираємо вершину з непарним степенем V₁ та ребро e₁. Додаємо ребро в ейлерів ланцюг. Видаляємо ребро e₁ з графа. Обираємо наступне ребро так, щоб воно не входило у попередню вершину V₁ та щоб воно не було мостом.

Продовжуємо операцію доти, доки не буле видалено усі ребра. Таким чином одержуємо ейлерів ланцюг e₁, e₁₅, e₁₇, e₁₉, e₂₀, e₂₅, e₁₃, e₁₄, e₁₂, e₁₆, e₁₈, e₂₆, e₂, e₃, e₉, e₆, e₁₀, e₁₁, e₅, e₈, e₇, e₂₂, e₂₄, e₄, e₂₃, e₂₁.

Визначимо хроматичне, реберне хроматичне та цикломатичне числа, для чого зробимо розфарбовування вершин та ребер графа. Розфарбуємо вершини графа.

Вершина v₈ має найбільший степінь. Присвоюємо їй колір1. Також колір1 присвоюємо вершинам v₁ та v₅, оскільки вони не суміжні з вершиною v₈ і не суміжні між собою. Обираємо вершину з найбільшим степенем з тих, що залишилися не розфарбованими. Це вершина v₃. Присвоюємо їй колір 2. Також колір 2 присвоюємо вершинам v₆, v₂ та v₉. Вершини v₇, v₄ та v₅ отримають колір 3.

Таким чином, вершини наведеного графа можна розфарбувати у 3 кольори. Отже, хроматичне число h(G)=3. Аналогічно знаходимо реберне хроматичне число H(G)=10.

Для визначення цикломатичного числа застосуємо формулу знаходження цикломатичного числа: ν (G)= m-n+р=26-9+1=18. Побудуємо заданий граф G та деяке відповідне до нього остове дерево Т (рис. 7.4).

Запишемо код дерева Т. Обираємо вершину з найменшим степенем V₂. Записуємо у код номер вершини, суміжної з вершиною V₂ – 7. Видаляємо з остовного дерева ребро e₂₀ та вершину V₂.

Знаходимо з кінцевих вершин вершину з найменшим степенем – V₅. У код записуємо 6. Видаляємо ребро e₁₇ та вершину V₅. Наступна кінцева вершина з мінімальним степенем V₆. Записуємо код 4. Видаляємо ребро e₁₅ вершину V₆. Продовжуємо до тих пір, доки не залишиться 2 вершини V₈ та V₉ і ребро e₁₃. Таким чином одержуємо код 7 – 6 – 4 – 1 – 3 – 8 – 8.

Побудуємо базис розрізів графа. Знайдемо ранг розрізів: χ(G)= m-ν =8.

Ранг розрізів відповідає кількості базисних розрізів для графа G.

e₂₀: V₁={ v₂ }; V₂={v₁, v₃, v₄, v₅, v₆, v₇, v₈, v₉},

c₁={ e₁₈, e₁₉, e₂₀, e₂₁, e₂₆};

e₂₅: V₁={ v₂, v₇ }; V₂={v₁, v₃, v₄, v₅, v₆, v₈, v₉ },

c₂={ e₁₈, e₁₉, e₂₂, e₂₃, e₂₄, e₂₅, e₂₆};

e₁₃: V₁={v₉}; V₂={v₁, v₂, v₃, v₄, v₅, v₆, v₇, v₈},

c₃={e₁₃, e₁₄};

e₅: V₁={v₂, v₇, v₈, v₉}; V₂={v₁, v₃, v₄, v₅, v₆},

c₄={e₄, e₅, e₆, e₁₀, e₁₁, e₁₂, e₁₈, e₁₉, e₂₂, e₂₃, e₂₆};

e₈: V₁={ v₂, v₃, v₇, v₈, v₉}; V₂={ v₁, v₄, v₅, v₆},

c₅={ e₇, e₈, e₉, e₁₀, e₁₁, e₁₂, e₁₈, e₁₉, e₂₆};

e₂: V₁={ v₁, v₂, v₃, v₇, v₈, v₉}; V₂={ v₄, v₅, v₆},

c₆={e₁, e₂, e₃, e₁₀, e₁₁, e₁₂, e₁₈, e₁₉};

e₁₅: V₁={ v₁, v₂, v₃, v₄, v₇, v₈, v₉}; V₂={ v₅, v₆},

c₇={ e₁₀, e₁₁, e₁₂, e₁₅, e₁₈, e₁₉};

e₁₇: V₁={ v₁, v₂, v₃, v₄, v₆, v₇, v₈, v₉}; V₂={ v₅},

c₈={ e₁₆, e₁₇, e₁₈, e₁₉}.

Побудуємо матрицю розрізів (табл. 9.15). Виразимо 3 небазисні розрізи через базисні.

с₉={e₂₅,e₅, e₄,e₆, e₁₀,e₁₁, e₁₂,e₂₄}

	с1	с2	с3	с4	с5	с6	с7	с8
e20	1
е25		1
е13			1
e5				1
е8					1
е2						1
е15							1
е17								1
е1						1
е3						1
е4				1
е6				1
е7					1
е9					1
е10				1	1	1	1
е11				1	1	1	1
е12				1	1	1	1
е14			1
е16								1
е18	1	1		1	1	1	1	1
е19	1	1		1	1	1	1	1
е21	1
е22		1		1
е23		1		1
е24		1
е26	1	1		1	1

Побудуємо базис циклів графа G. Кількість базисних циклів відповідає цикломатичному числу для заданого графа. Отже, у заданому графі є 18 базисних циклів.

Для побудови базису циклів додаємо до остовного дерева Т кожну з хорд

у порядку їхнього зростання, виділяємо простий цикл і формуємо базис циклів графа (у вигляді послідовності ребер, що утворять кожний з базисних циклів).

Таким чином отримуємо 18 базисних циклів.

Виразимо 3 небазисні цикли через базисні.