Тема 2. Основные теоремы теории вероятностей

1 вопрос. Алгебра событий. Вероятность суммы и произведения событий.

2 вопрос. Вероятность появления хотя бы одного события.

3 вопрос. Формула полной вероятности.

4 вопрос. Вычисление вероятностей гипотез. Формула Байеса.

5 вопрос. Формула Бернулли. Повторные испытания.

6 вопрос. Вероятнейшее (наивероятнейшие) число появлений событий.

1 вопрос. Алгебра событий. Вероятность суммы и произведения событий.

Непосредственный подсчет вероятностей по классическому или статистическому определению для решения многих практических задач достаточно труден. Поэтому возникла необходимость в разработке методов вычисления вероятностей событий, позволяющих по известным вероятностям одних событий определять вероятности наступления других событий. Эти методы связаны с нахождением вероятностей суммы и произведения событий. Однако прежде чем мы начнем вычислять такого рода вероятности, рассмотрим основные понятия алгебры событий (алгебры Буля, Англия XIX), а именно понятие суммы событий и произведения событий.

Произведением нескольких событий A₁,A₂,…,A_n называется событие Е, состоящее в их совместном наступлении: Е=А1*А₂*А₃*...*Аn

Если речь идет о 2-х событиях А и В, то А и В=и А и В =А*В=Е. (А В)

Суммой событий А и В (события совместные) называется событие S=A+B, которое состоит в появлении хотя бы одного из этих событий, т.е. или событие А, или событие В, или двух этих событий вместе и А и В. (Принцип Лапласа), А+В= или А или В или А*В (А В). Т.е. сумма событий включает в себя и сумму, и произведений событий.

Если А и В - несовместные события, то А и В = А*В=Ø. Т. обр., если события А и В - несовместные, то сумма S, равная А+В, будет означать «или А или В», т.к. для несовместных событий (А и В) - есть событие невозможное.

Разностью 2-х событий А и В называется событие, которое состоится, если событие А произойдет, а событие В не произойдет (А\В).

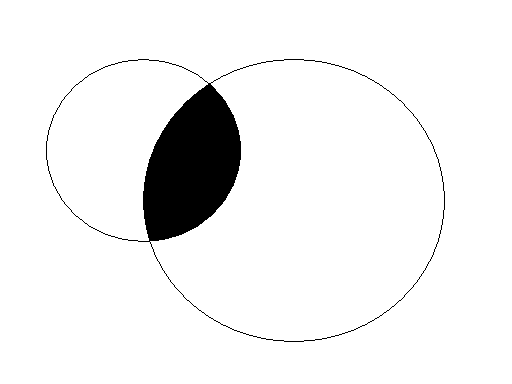
Дадим геометрическую интерпретацию основных действий над событиями с помощью диаграмм Вена.

1. А		2. В		3. А+В		АВ
5.		6.		7. А-В=А		8. В-А=В
9.		10.

Операции сложения и умножения событий обладают следующими свойствами:

1. А+В=В+А – коммутативность сложения

2. А+(В+С)=(А+В)+С – ассоциативность сложения

3. АВ=ВА – коммутативность умножения

4. А(ВС)=(АВ)С – ассоциативность умножения

Вероятность суммы несовместных событий - вероятность суммы 2-х несовместных событий А и В равна сумме вероятностей этих событий, т.е. Р(А+В)=Р(А)+Р(В).

Вероятность суммы совместных событий - вероятность суммы 2-х совместных событий А и В равна сумме вероятностей этих событий без вероятностей их совместного наступления, т.е. Р(А+В)=Р(А)+Р(В)-Р(А*В).

Сумма вероятностей событий, образующую полную группу, всегда равна 1. Если события А1,А2,…,Аn образуют полную группу, то Р(А1)+Р(А₂)+...+Р(Аn)=1 или

Сумма вероятностей противоположных событий, всегда равна 1, т.е. Р(А)+Р(Ā)=1

ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СОБЫТИЯ. УСЛОВНЫЕ И БЕЗУСЛОВНЫЕ ВЕРОЯТНОСТИ.

Два события А и В называются независимыми, если вероятность наступления каждого из них не зависит от того, произошло или нет другое событие. В этом случае вероятность каждого из событий называется безусловной.

Два события А и В называются зависимыми, если вероятность каждого из событий (и А и В) зависит от появления другого события. Вероятности таких событий называются условными, определенными при условии, что одно из событий произошло.

Если рассматриваются не 2 события, а несколько событий, зависимых или независимых между собой, то такие события называются зависимыми или независимыми в совокупности.

Вероятность произведения 2-х независимых событий А и В равна произведению вероятностей этих событий, Р(А*В)=Р(А)*Р(В).

Вероятность произведения 2-х зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, Р(А*В)=Р(А)*Р_А(В)=Р(В)*Р_В(А)

Если рассматриваются не 2, а совокупность независимых событий, то вероятность их произведения находится аналогично вероятности произведения 2-х событий.

Вероятность произведения нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных событий, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже произошли, т.е. P(A1*A2*A3….An)= P(A1)*P_A1(A2)*P_А1А2(A3)…