2. Моделювання роботи лдс в z-області

Моделювання роботи фільтру в z-області передбачає розрахунок передавальної функції, що представлена одним з наступних виглядів (див. лекцію 5):

• Загальний – дробово-раціональна функція (7).

• Добуток простіших множників першого ступеню – із розкладанням за нулями та полюсами

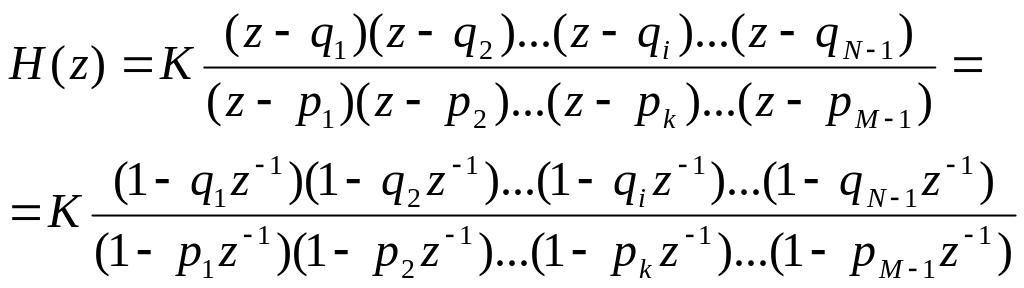(11)

де - коефіцієнт підсилення; - дійсний чи комплексний корінь чисельника (нуль); - дійсний чи комплексний корінь знаменника (полюс); - кількість нулів та полюсів.

• Добуток простіших множників другого ступеню

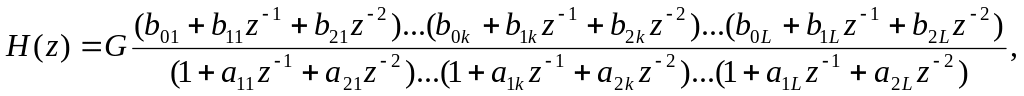(12)

де - номер комплексно-спряженої пари нулів або полюсів; - коефіцієнт підсилення; - кількість комплексно-спряжених пар нулів та полюсів,

• Сума простих дробів

(13)

або через від’ємні степені

(14)

де - константа чисельника; - ціла частина .

Розглянемо взаємні перетворення даних різновидів представлення ПФ.

2.1. Представлення передавальної функції в загальному вигляді

Загальний вигляд ПФ – дробово-раціональна функція (7) – представляється за допомогою векторів коефіцієнтів чисельника й знаменника в порядку зменшення від’ємних степенів, починаючи з коефіцієнту при нульовій степені.

Позначимо:

вектор коефіцієнтів чисельника

num=b=[b0 b1 … bN-2 bN-1]

довжиною N; num від слова numerator (чисельник),

вектор коефіцієнтів знаменника

den=a=[1 a1 a2 … aM-2 aM-1]

довжиною M; den від слова denominator (знаменник).

2.2. Представлення передавальної функції загального вигляду у вигляді добутку простіших множників першої ступені й навпаки: функції tf2zp, zp2tf

Якщо передавальна функція задана в загальному вигляді (7), то для її представлення у вигляді простіших множників першої степені (11) необхідно визначити корені чисельника (нулі) й корені знаменника (полюси), тобто корені поліномів, що задані векторами num=b й den=a відповідно. Корені поліномів можна розрахувати за допомогою функції roots окремо для поліномів чисельника й знаменника, проте в MATLAB присутня спеціальна функція tf2zp, що забезпечує розрахунок нулів й полюсів. Формат функції tf2zp має вигляд

[q,p,K]=tf2zp(num,den)

де для ЛДС з одним входом та виходом:

- вектор нулів; - вектор полюсів; - коефіцієнт підсилення; - вектор коефіцієнтів чисельника ПФ (7) в порядку зменшення степенів, починаючи з коефіцієнту при нульовій степені; - вектор коефіцієнтів знаменника ПФ (7) в порядку зменшення степенів, починаючи з коефіцієнту при нульовій степені; перший елемент вектора завжди рівний одиниці.

Приклад 8: Визначити нулі й полюси НІХ-фільтру 2-го порядку, що має ПФ

(15)

>> num=[1 1 1];

>> den=[1 -0.7 0.25];

>> [q,p,K]=tf2zp(num,den)

q =

-0.5000 + 0.8660i

-0.5000 – 0.8660i

p =

0.3500 + 0.3571i

0.3500 – 0.3571i

K = 1

Запишемо ПФ у вигляді добутку (11) за допомогою отриманих значень нулів й полюсів

(16)

Виразимо нулі й полюси через радіус й кут (модуль та аргумент). Введемо позначення:

r0, rp – радіуси нулів й полюсів,

f0, fp – кути нулів й полюсів.

>> r0=abs(q(1))

r0 = 1.000

>> f01=angle(q(1))

f01 = 2.0944

>> f02=angle(q(2))

f02 = -2.0944

>> rp=abs(p(1))

rp = 0.5000

>> fp1=angle(p(1))

fp1 = 0.7954

>> fp2=angle(p(2))

fp2 = -0.7954

Запишемо ПФ через виражені таким чином нулі й полюси

(17)

Обернена процедура – перетворення ПФ, що представлена через нулі й полюси (11), в дробово-раціональну функцію (7) виконується за допомогою оберненої функції zp2tf, формат якої має вигляд

[num,den]=zp2tf(q,p,K)

Для вищенаведеного прикладу:

>> q = [(-0.5000+0.8660i) (-0.5000-0.8660i)]’;

>> p = [(0.3500+0.357i) (0.3500-0.3571i)]’;

>> K=1;

>> [num,den]=zp2tf(q,p,K)

num = 1.0000 1.0000 1.0000

den = 1.0000 -0.7000 0.2500