Лабораторна робота №2
„Моделювання обробки сигналів лінійною дискретною системою в програмному середовищі MATLAB”
Обладнання: Персональний комп’ютер, програмне середовище MATLAB 6.5
Мета й завдання: Дослідити роботу лінійної дискретної системи в часовій, z-області та частотній області.
Математичне моделювання обробки сигналів лінійною дискретною системою (ЛДС) включає:
розрахунок характеристик ЛДС у часовій, частотній та z-областях;
розрахунок реакції ЛДС за співвідношенням вхід-вихід;
аналіз впливу та реакції у часовій та частотних областях.
Приведемо у відповідність термінологію й позначення, що були використані раніше, із загальноприйнятими в MATLAB.
В MATLAB математичною моделлю ЛДС називають описання співвідношення вхід-вихід у вигляді рівняння чи системи рівнянь, що дозволяють розрахувати реакцію на заданий вплив.
У часовій області співвідношення вхід-вихід може описуватися за допомогою (див. Лекцію 4):
Різницевого рівняння (РР)
(1)
яке задається вектором
коефіцієнтів впливу
(2)
та вектором коефіцієнтів реакції
.
(3)
Перший елемент вектора
завжди рівний 1
.
(4)
Формули згортки
(5)
де імпульсна характеристика й вплив задаються у вигляді кінцевих послідовностей (векторів).
Системи рівнянь змінних стану
(6)
де
-
змінні стану;
- вхідний сигнал;
- для систем з одним входом та одним
виходом – квадратна матриця розміром
,
де
- порядок ЛДС;
- вектор-стовбчик;
- вектор-рядок;
- скаляр.
Передавальна функція ЛДС (див. Лекцію 5)
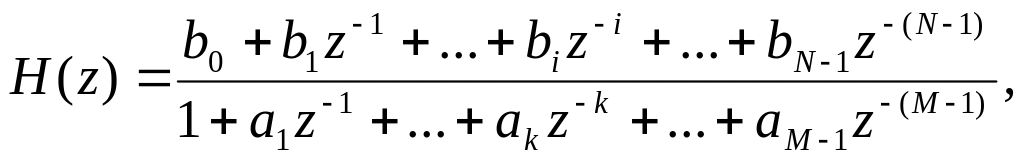(7)
подібно до РР, задається векторами коефіцієнтів (2) та (3).
Частотна характеристика ЛДС представляється через модуль (АЧХ) й аргумент (ФЧХ) (див. Лекцію 6)
.
(8)
В подальшому найменування „ЛДС” та „цифровий фільтр” (ЦФ) будемо вважати тотожніми.
1. Моделювання роботи лдс у часовій області
Моделювання роботи ЛДС у часовій області виконується на основі однієї з її математичних моделей, приведених вище.
1.1. Моделювання роботи лдс на основі різницевого рівняння(рр): функція filter
Моделювання роботи ЛДС на основі РР (1) – розрахунок реакції на початковий вплив при нульових початкових умовах (НПУ) – виконується за допомогою функції filter, формат якої має вигляд:
filter(b,a,x)
де
-
вектор коефіцієнтів (2) в порядку їх
слідування,
- вектор коефіцієнтів (3) в порядку їх
слідування; перший елемент завжди рівний
1,
- вектор відліків впливу
.
Розглянемо два приклади ЛДС – СІХ- та НІХ-фільтри.
Приклад 1. Розрахувати реакцію СІХ-фільтра 2-го порядку, заданого наступним РР
(9)
де
>> b=[0.1 0.5 0.7];
>> a=[1];
>> n=0:32;
>> x=sin(0.5.*n);
>> y=filter(b,a,x);
>> plot(n,x,n,y,’--’), grid
>> hold on
>> stem(n,x)
>> stem(n,y)
>> gtext (‘x(n)’)
>> gtext (‘y(n)’)
Результати розрахунків представлені на Рис.1, де окрім дискретних сигналів зображено їх огинаючі.
Рис.1. Вхідний та вихідний сигнали (до прикладу 1)
Приклад 2. Розрахувати реакцію НІХ-фільтру 2-го порядку, заданого наступним РР
(10)
де
>> b=[1 1 1];
>> a=[1 0.7 -0.25];
>> n=0:32;
>> x=sin(0.5.*n);
>> y=filter(b,a,x);
>> plot(n,x,n,y,’-’), grid
>> hold on
>> stem(n,x)
>> stem(n,y)
>> gtext (‘x(n)’)
>> gtext (‘y(n)’)
Рис.2. Вхідний та вихідний сигнали (до прикладу 2)
1.2. Розрахунок імпульсної характеристики (іх) за допомогою різницевого рівняння(рр): функція filter
Для того, щоб розрахувати ІХ НІХ-фільтра за допомогою РР (1), необхідно в якості впливу обрати одиничний цифровий імпульс – вектор [1 0 ...], де кількість нулів відповідає довжині ІХ (в дійсності нескінченної).
Приклад 3. Розрахувати ІХ НІХ-фільтра, заданого РР (10). Введемо позначення: h – ІХ, delta – одиничний цифровий імпульс довжиною 51 відліків (одиниця та 50 нулів):
>> b=[1 1 1];
>> a=[1 0.7 -0.25];
>> delta=[1; zeros(50,1)]’;
>> h=filter(b,a,delta);
>> stem(0:length(delta)-1,h)
>> grid
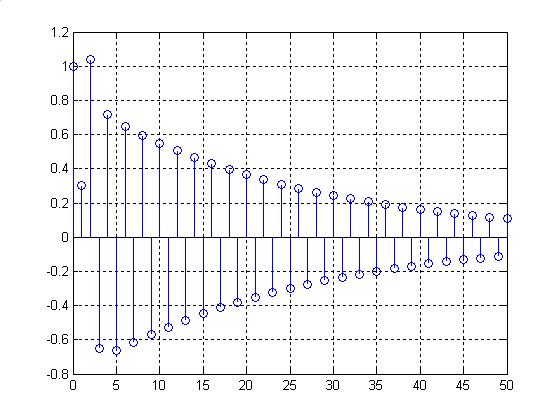
Рис.3. ІХ, розрахована за РР (до прикладу 3)
1.3. Розрахунок імпульсної характеристики (іх) за допомогою коефіцієнтів різницевого рівняння (рр): функція impz
ІХ може бути розрахована безпосередньо за коефіцієнтами РР за допомогою функції impz, формат якої має вигляд
[h, nT]=impz(b,a,N,Fs)
де
- вектор коефіцієнтів (2) в порядку їх
слідування,
- вектор коефіцієнтів (3) в порядку їх
слідування; перший елемент завжди
рівний 1,
- кількість відліків ІХ, що розраховується
(оскільки ІХ нескінченна),
- частота дискретизації в Гц,
- вектор-стовбчик відліків ІХ,
- вектор-стовбчик значень дискретного
часу.
Визначимо ІХ НІХ-фільтру за даними попереднього прикладу при =50 та =2000Гц:
>> b=[1 1 1];
>> a=[1 0.7 -0.25];
>> N=50;
>> Fs=2000;
>> [h,nT]=impz(b,a,N,Fs);
>> stem(nT,h),grid
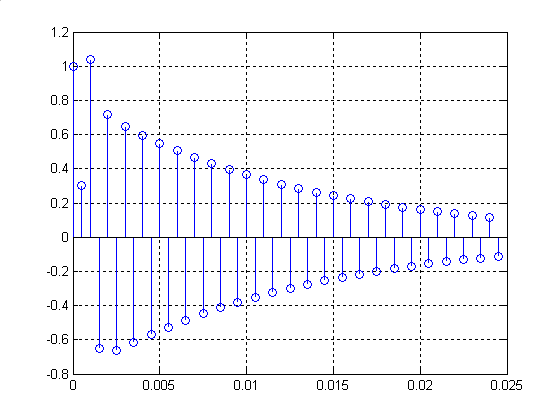
Рис.4. ІХ, розрахована за коефіцієнтами РР (вісь )
Графік ІХ (Рис.4) має такий самий вигляд як і в попередньому випадку (при розрахунках за допомогою функції filter), за виключенням того, що замість осі нормованого часу ми маємо вісь .
Якщо необхідна вісь
,
зручніше використати інший формат
функції impz
h=impz(b,a,N)
Для прикладу, що розглядається (див. Рис.5):
>> h=impz(b,a,50);
>>n=1:50;
>>stem(n,h),grid
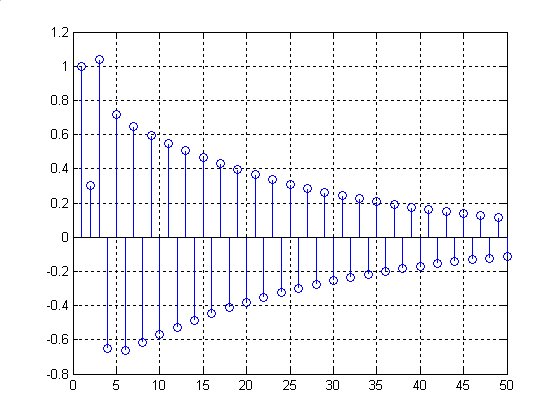
Рис.5. ІХ, розрахована за коефіцієнтами РР (вісь )