Xlabel('Час, с'); ylabel('Рівень'); % напису уздовж осей

grid on % координатна сітка

Як бачимо, тепер числові значення вхідних даних задаються як аргументи m-функції ton_sig.m. Вихідні дані функції використовуються для побудови графіка.

Очевидно, застосування m-функцій вигідно тоді, коли алгоритм формування значень функції досить складний: міститься багато команд і звертань до різноманітних бібліотечних функцій з непростим синтаксисом.

Очевидний і недолік m-функцій – необхідно пам'ятати їх синтаксис. Втім, одержати потрібну інформацію можна, якщо в командному вікні задати команду help:

>> help ton_sig

У результаті на моніторі відобразиться коментар, з якого починається m-функція. Для наведеного вище приклада текст допомоги має такий вигляд:

%-і-і-і-функція ton_sig.m -і-і-і-і-і-

% [s,t]=ton_sig(B,f1,Fi1,Fs,N1)

%-і-і-і-і-і-і-і-і-і-і-і-і-і-і-і-і-і-і-і-

% генерування гармонійного сигналу

% y = B * sin(2*pi*f1*x + Fi1),

% B - амплітуда;

% N1 - кількість відліків сигналу;

% f1 - частота;

% Fs - частота дискретизації;

% Fi1 - початкова фаза сигналу

%-і-і-і-і-і-і-і-і-і-і-і-і-і-і-і-і-і-і-і-

Таким чином, очевидний висновок: дуже важливо при програмуванні m-функцій оздоблювати їх якісним і докладним коментарем.

4. Моделювання дискретних сигналів в Simulink

Генерування сигналів в Simulink, природно, має свої особливості. Розглянемо їх. Візьмемо з бібліотеки блоків Simulink два блоки: Sine Wave (з розділу Sources) і Scope (з розділу Sinks). З'єднавши їх, одержимо наступну схему (Рис.2).

Рис.2

Потім подвійним натисканням на блоці осцилоскопа активізуємо вікно, що імітує екран осцилоскопа, і запустимо модель (кнопка Start simulation). У результаті одержимо зображення відрізка синусоїди (Рис.3).

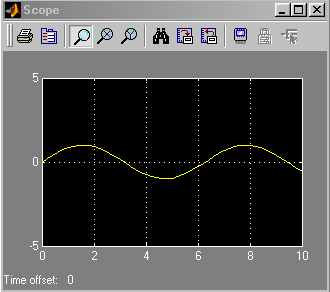
Рис.3

Як бачимо, генерувати гармонійний сигнал у середовищі Simulink навіть простіше, ніж у середовищі Matlab. Однак це перше враження досить оманливе. Дійсно, адже важливо ще вміти управляти параметрами гармонійного сигналу. Дійсно, за замовчуванням амплітуда генерованого сигналу прийнята рівній одиниці. Однак частотою, початковою фазою й тривалістю сигналу ми поки не керуємо.

Двічі клацнемо по блоці Sine Wave – у результаті з'явиться вікно настроювань параметрів (Рис. 4). Клацнувши по кнопці Help, одержимо інструкцію з даного блоку, сутність якої зводиться коротенько до того, що в даному блоці виконується операція

З наведеної формули й написів на мал.5 стає зрозумілим зміст чотирьох змінних: амплітуди, кутової частоти, початкової фази й постійній складовій. Залишається поки зашифрованим зміст змінної “час”.

Зупиняючись на цьому важливому питанні, відзначимо розходження понять “час” й “модельний час”. Так, генерування відрізка сигналу тривалістю 1с (модельний час) може тривати значно більше короткий проміжок часу, наприклад, 0.1с (реальний час). Швидкість генерування залежить від обсягу обчислень, швидкодії комп'ютера, від обраного алгоритму моделювання, і т.д. До речі, цілком можливий зворотний ефект - для складного алгоритму процедура моделювання відрізка сигналу тривалістю 0.1с може розтягтися на кілька секунд.

Сигнал може генеруватися двох типів: неперервний time-based і дискретний sample-based. Для моделювання роботи незперервних систем рекомендують використовувати неперервний тип time-based, а для моделювання роботи дискретних систем – дискретний тип sample-based [2].

Якщо встановлено тип time-based, тоді параметр Sample time може приймати значення:

• 0 (за замовчуванням) - блок працює в неперервному режимі;

• >0 - блок працює в дискретному режимі;

• -1 - блок успадковує той же режим, що й приймаючий блок.

Як вказується в Help, робота в неперервному режимі може приводити до більших похибок генерації на більших проміжках модельного часу.

Робота в дискретному режимі змушує блок поводитися так, ніби до виходу неперервного генератора був приєднаний блок Zero-Order Hold. Дійсно, зібравши дві схеми (Рис. 5) і задавши в обох випадках значення параметра Sample time, рівне 0.5 (вікно настроювання блоку Zero-Order Hold показане на Рис. 6), одержуємо ідентичні результати (Рис. 7).

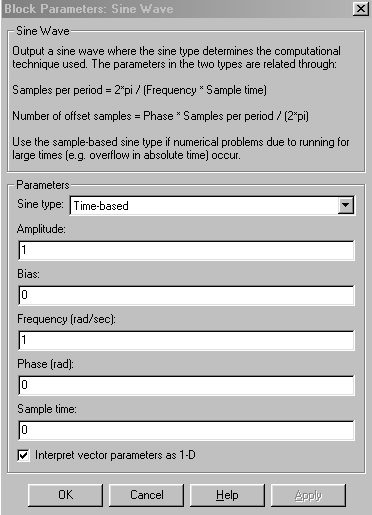
Рис.4

Рис.5

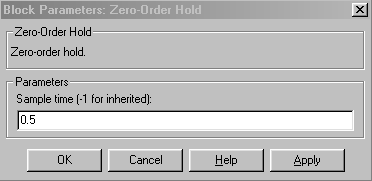
Рис.6

Рис.7

Таким чином, блок Zero-Order Hold можна трактувати як “дискретизатор”, тобто частина АЦП, відповідальну за дискретизацію сигналу. Іноді блок Zero-Order Hold називають АЦП [4]. На нашу думку, це не коректно, оскільки дискретизований сигнал у “справжньому” АЦП піддається ще й квантуванню за рівнем. У блоці Zero-Order Hold, однак, квантування не здійснюється.

Кілька слів про побудову графіків. Крім блоку Scope, графік можна побудувати й за допомогою блоку X-Y-Graf, на верхній вхід X якого потрібно подати послідовність моментів часу за допомогою блоку Clock (годинник), а на нижній вхід Y – значення генерованого сигналу (Рис. 8).

Рис.8

У результаті попередньо налаштований (у відповідному вікні настроювання задаються граничні значення аргументу й функції, а також указується значення параметра Sample time) графобудівник видасть показаний на Рис. 9 графік, якщо для блоку X-Y-Graf заданий Sample time=-1 (тобто період дискретизації успадковується).

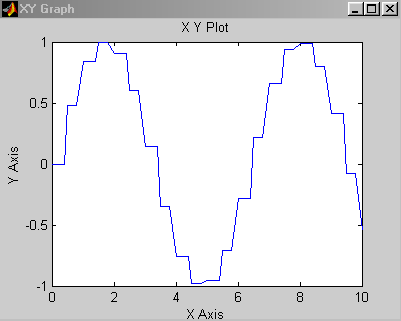
Рис.9

Графік буде трохи іншим (Рис. 10), якщо для блоку X-Y-Graf задане Sample time=0.5.

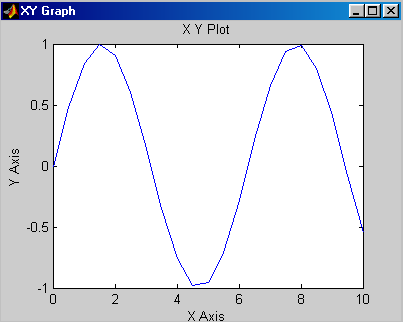
Рис.11

Ще про один спосіб побудови графіків. Масиви відліків моментів часу й відповідних значень сигналу можна за допомогою блоку To Workspace експортувати із середовища Simulink у середовище Matlab (Рис. 12).

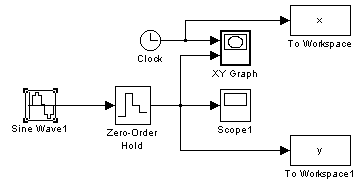
Рис.12

При цьому, як показує практика, найкраще задати формат array для експортованих даних (Рис. 13).

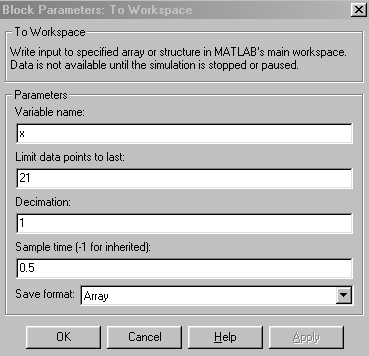
Рис.13

Подальша побудова графіка в середовищі Matlab відбувається за допомогою команди plot(x,y) (Рис. 14).

Рис.14

Підсумуємо результати проведених дослідів.

Сигнал типу time-based при роботі блоку генерації в режимі неперервного часу має вигляд гладкої функції часу, а в режимі дискретного часу - вигляд східчастого сигналу, такого, як якби до виходу генератора плавного сигналу був приєднаний блок Zero-Order Hold, що є дискретизатором типу “відлік-зберігання”.

Іншими словами, задаючи режим дискретного часу, ми йдемо від необхідності використання блоку Zero-Order Hold.

Згенеруємо в Simulink відрізок дискретного гармонійного сигналу з тими самими параметрами, що були задані в Matlab: амплітуда 1, частота 100 Гц, частота дискретизації 1000 Гц, початкова фаза , кількість відліків 20.

Збираємо знову схему з генератора й осцилоскопа. У вікні-масці настроювання генератора робимо вказуємо потрібні числові значення параметрів, задаємо тип time-based і привласнюємо значення Sample time = 0.001 (Рис. 15).

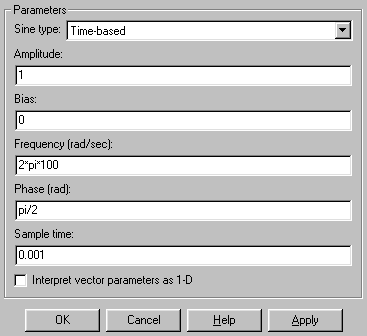
Рис.15

Після запуску моделі одержуємо на екрані осцилоскопа зовсім не ту картину, що очікували (Рис.16).

Рис.16

Причина проста – потрібно ще настроїти параметри моделювання: задати початок і кінець модельного часу (у нашому випадку це 0 й 0.02с, відповідно), а також вибрати алгоритм моделювання. На Рис. 17 показане вікно настроювань параметрів моделювання, що активізується при виборі позиції меню Simulation/Simulation parameters.

Рис.17

Крім того, налаштуємо параметри осцилоскопа, клацнувши по кнопці Parameters на вікні Scope (Рис. 18).

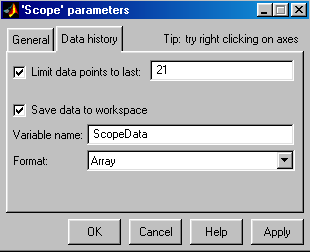
1. b)

Рис.18

Після запуску моделі на екрані осцилоскопа з'явиться зображення (Рис.19).

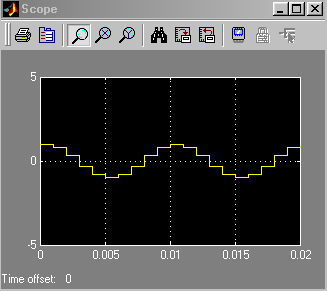
Рис.19

Оскільки параметри осцилоскопа були задані так, щоб у робочий простір виводився двовимірний масив ScopeData значень аргументу й функції, за допомогою команд

>> y1=ScopeData(:,1);

>> y2=ScopeData(:,2);

>> plot(y1,y2)

можна побудувати графік функції засобами Matlab (Рис. 20).

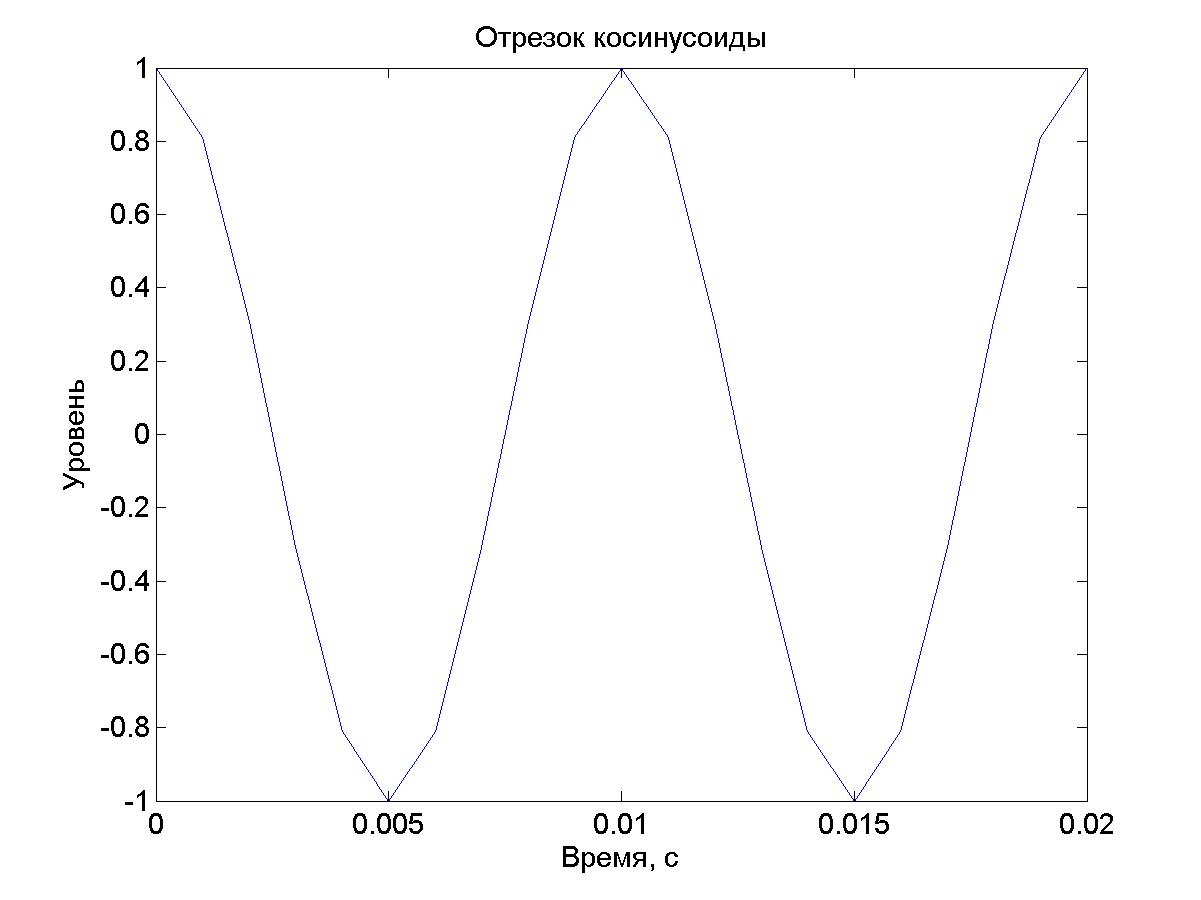
Рис.20

Список літератури

1. Продеус А.Н., Родінова М.В. Безпаперова технологія проведення практикумів із статистичної обробки сигналів. – Электроника и связь, №20, 2003, pp.117-120

2. Гультяев А. Имитационное моделирование в среде Windows. – С-Пб, КОРОНА принт, 1999. – 287 с.

3. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. – М.,С-Пб,К., изд.дом «Вильямс», 2003. – 1092 с.

4. Калюжний О.Я. Моделювання систем передачі сигналів в обчислювальному середовищі MATLAB-Simulink. – К., “Політехніка”, 2004. – 135 с.

14