6.3. Движущие процессы кристаллизации Термодинамический анализ процесса зарождения

Условно можно выделить равновесные, квазиравновесные и кинетические модели, описывающие механизм зарождения и роста объемных кристаллов и слоев с учетом термодинамиче­ского, квантово-механического и молекулярно-статистического анализов элементарных актов. Различные модели кристалли­зации дополняют друг друга и различаются учетом разных про­цессов: движения фазовой границы, распределения агрегатов по размерам на поверхности, заполнения узлов кристаллической решетки и т. д.

Имеется определенная связь между уровнем развития техно­логии и развитием отдельных теоретических моделей. Так, до появления микроэлектроники, пленочной и эпитаксиальной тех­нологии преобладал термодинамический подход. Это связано с тем, что объектом исследований был медленно растущий кри­сталл (в условиях, близких к равновесным) или естественный (природный) кристалл. Использование кинетических моделей было затруднено без применения ЭВМ.

При кристаллизации на атомно-гладких поверхностях кристаллы возникают в результате двух элементарных процессов, не зависящих от того, происходит ли кристаллизация из паро­вой, жидкой или твердой фазы:

1) в результате возникновения способного к росту зародыша субмикроскопического размера;

2) вследствие разрастания и превращения этого зародыша в макроскопический кристалл, ограниченный поверхностями, ха­рактерными для соответствующего кристалла и условий роста.

Предпосылкой для возникновения кристаллических зароды­шей из неупорядоченной гомогенной фазы является наличие движущей силы процесса — пересыщения или переохлаждения.

При этом следует делать различие между гомогенным и ге­терогенным образованием зародышей. При гомогенном образо­вании зародышей имеет место фазовый переход (например, расплав—кристалл) при отсутствии границ раздела, т. е. внут­ри самой фазы за счет случайных колебаний плотности и кинетической энергии без участия посторонних поверхностей раздела. Если кристаллизация происходит на стенках сосуда, на других кристаллах (т. е. при участии посторонних поверх­ностей раздела), говорят о гетерогенном образовании зароды­шей.

Весьма часто необходимо значительное пере­охлаж­дение или пересыщение, чтобы вызвать образование за­роды­шей. Это становится понятным, если учесть, что для воз­никновения за­родышей необходимо затратить энергию или со­вершить работу (ра­боту образования зародышей), которая имеет смысл энергии актива­ции.

Если, например, пересыщение недостаточно велико, то за­родыш может не образоваться, тогда фазовый переход не произойдет. Если же во время фазового перехода кристалличе­ская фаза уже имеется, например в форме заранее внесенных кристаллов, то величина работы образования зародышей зна­чительно снижается, и фазовый переход происходит уже при меньших пересыщениях.

Гомогенное образование зародышей. Термодинамический анализ образования зародышей из гомогенной фазы, например из расплава, основан на установлении изменения энергии Гиббса системы, происходящего при фазовом переходе. Рас­смотрим изменение энергии Гиббса чистого вещества как функцию температуры (рис. 6.8). Энергия Гиббса обеих фаз (кристалла и его расплава) в точке плавленияТ_плодинакова. НижеТ_плустойчива кристаллическая фаза, так как она обла­дает меньшей энергией Гиббса. ВышеТ_плтермодинамически устойчив расплав по той же причине. С термодинамических по­зиций фазовый переходрасплав - кристаллвозможен уже при бесконечно малом переохлаждении, так как он обеспечивает уменьшение энергии Гиббса. Практически же фазовый переходрасплав - кристаллнаступает при значительно большемТ.

Причина задержки фазового превращения заключается в том, что возникновение кристаллической фазы связано не толь­ко с изменением объема, но и с образованием новой поверхно­сти раздела. Изменение энергии Гиббса G_п, связанное с обра­зованием поверхности новой фазы, является положительным, а объема G_об — отрицательным. По этой причине положительное изменение свободной энергии противодействует процессу фазо­вого перехода расплав - кристалл.

Рис.6.8. Зависимость энергии Гиббса кристалла (1) и его расплава (2) от температуры

Рис.6.9. Зависимость энергии образования зародыша от его радиуса

Кроме того, следует учитывать изменение энергии Гиббса G_деф, которое связано с упругой деформацией зародышей при фазовом переходе.

Общее изменение энергии Гиббса образования зародышей оказывается суммой трех слагаемых:

, (6.8)

где ΔG_об - объемная составляющая; ΔG_n - поверхностная со­ставляющая.

Энергия деформации должна учитываться лишь при образо­вании зародышей новой фазы внутри твердой фазы, например при полиморфных фазовых превращениях, при кристаллизации стекол или в процессах осаждения. Без учета деформационного слагаемого уравнение запишется в виде .

Изменение ΔG_об пропорционально объему возникающей фа­зы V~r³; изменение ΔG_п пропорционально поверхности s ~ r², где r — радиус зародышей. Определим для частного случая (шарообразный зародыш радиусом r) величины ΔG_об и ΔG_п. Обозначим через G^ж энергию Гиббса расплава, приходящуюся на единицу объема, а через G^к — соответствующую энергию Гиббса кристалла. Тогда

, (6.9)

где Δq_об - удельное изменение объемной энергии при фазовом переходе.

Известно, что ΔG = ΔH -TΔS, а для энтропии плавления можно принять S_пл=Н_пл/Т_пл. Отсюда получим

(6.10)

. (6.11)

Аналогичным образом получим выражение для ΔG_п:

, (6.12)

где σ_к-ж - межфазная энергия границы раздела кристалл - расплав.

Тогда общее изменение энергии Гиббса запишется в виде

. (6.13)

Из выражений (6.9), (6.12), (6.13) следует, что ΔG_об, ΔG_п и ΔG являются функциями радиуса зародыша r, зависимости которых представлены на рис. 6.9. Максиму­му на кривой ΔG соответствует критический радиус зароды­ша r*. Критическим считается зародыш такого размера, при котором вероятности отрыва и присоединения атома к нему равны.

Зародыш, который меньше этой величины, нестабилен и растворяется вновь, так как его увеличение связано с повышением энергии Гиббса. Зародыш с радиусом больше r*, напротив, устойчив и способен расти, так как при присоединении к нему атомов ΔG уменьшается. Зародыши с r<r* называются субзародышами, а с r>r*— сверхзародышами. Величина r* находится из ус­ловия

. (6.14)

Отсюда получим

. (6.15)

После подстановки выражения (6.15) в выражение (6.13) получим уравнение для изменения энергии Гиббса при образо­вании зародыша критического размера:

. (6.16)

Критический радиус r* является функцией переохлаждения ΔT. Чем больше ΔT, тем меньше становится r*, т. е. чем боль­ше переохлаждение, тем меньше по размерам могут быть заро­дыши, которые способны расти.

Поскольку изменение ΔG на стадии образования критиче­ского зародыша положительно (рис. 6.9), то для возник­новения зародышей необходимо затратить работу, так называемую работу образования зародышей A₃. Величина этой ра­боты зависит от величины зародыша. Работа образования за­родыша должна производиться вплоть до достижения крити­ческого размера r*. В этом случае A_з=ΔG^*. Только после это­го система начнет самопроизвольно переходить в устойчивое состояние с выделением энергии.

Анализ процесса гомогенного зарождения показывает, что работа образования зародыша является не единственным фак­тором, определяющим скорость его образования. Для вязких расплавов скорость этого процесса зависит еще и от вероятно­сти перехода атомов из расплава в зародыш, т. е. вероятности преодоления энергетического барьера путем диффузии атомов в переходном слое. Тогда скорость образования зародышей за­пишется в виде

, (6.17)

где ΔG_диф - энергия Гиббса процесса диффузии.

Зависимость (6.17) имеет максимум (рис. 6.10). Наличие максимума скорости образования зародышей можно объяснить следующим образом. С понижением температуры (т. е. с уве­личением переохлаждения ΔТ) работа образования зародышей уменьшается, что приводит к увеличению скорости образования зародышей. Вместе с тем происходит повышение вязкости рас­плава, что уменьшает диффузионную подвижность атомов в нем. Это приводит к уменьшению скорости образования заро­дышей.

Гетерогенное образование зародышей. При гетерогенном зарождении необходимо учитывать силы межатомного взаимо­действия между частицами как внутри маточной фазы, так и с подложкой. Соотношение этих сил и определяет краевой угол смачивания капельки (зародыша) θ материнской фазы на подложке (рис. 6.11).

Рис.6.10. Зависимость скорости образования зародышей от переохлаждения расплава: 1 – диффузионная (вязкостная) область; 2 – область, в которой процесс кристаллизации лимитируется зарождением; 3 – метастабильная область

Рассмотрим термодинамическую теорию гетерогенного об­разования зародышей на примере кристаллизации из паровой фазы. Схема взаимодействия пара и подложки дана на рис. 6.12. Представим атомно-гладкую подложку, находящуюся в среде однородного пересыщенного пара или в условиях, когда на нее падает молекулярный пучок. В этом случае пред­полагается возникновение зародыша критических размеров (рис. 6.12, положение 4), который способен расти самопро­извольно с уменьшением энергии Гиббса.

Рис.6.11. Форма зародышей кристаллической фазы: а – шаровой сегмент; б – шестигранник; в - диск

Форма зародышей, а значит, и их энергия образова­ния Гиббса зависят от поверхностной энергии подложки. У кристаллов с изотропной (или слабо анизотропной) поверхностной энер­гией зародыш имеет форму сферического купола (рис. 6.11,а). У более анизотропных кристаллов критические зародыши могут быть в форме диска или многогранника (рис. 6.11,в, б). Для простоты рассмотрим куполообразный сферический зародыш. Если учитывать лишь поверхностные энергии и считать, что даже малый зародыш обладает объем­ными свойствами, то форма зародыша зависит от контактного угла θ, определяемого из капиллярной теории выражением

, (6.18)

где σ_п-к, σ_к-з, σ_з-п - межфазные энергии в системе пар - кри­сталл, кристалл - зародыш, зародыш - пар соответственно.

Выведем выражение для критического значения энергии Гиббса ΔG_i*. Энергия Гиббса образования зародыша, содер­жащего i атомов, состоит из двух слагаемых — объемного и по­верхностного. Складывая энергии, относящиеся к разным по­верхностям раздела купола и используя выражение (6.18), получим для поверхностного члена

(6.19)

где f(θ)– геометрический фактор, определяемый из выражения

. (6.20)

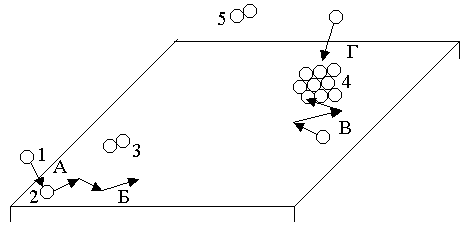
Рис.6.12. Схема взаимодействия пара и подложки: 1 – атом в паре; 2 – адсорбированный атом; 3 – адсорбированная двухатомная частица; 4 – зародыш докритического размера; 5 – двухатомная частица в паре; А – процесс адсорбции; Б – поверхностная диффузия; В – рост зародыша за счет поверхностной диффузии атомов; Г – рост зародыша за счет атомов из паровой фазы

Объемный член определяется выражением

, (6.21)

где Δq_a — удельное объемное изменение энергии Гиббса при образовании зародыша из пересыщенного адсорбционного слоя адатомов, определяемое как

,

или

, (6.22)

где V_а — атомный объем; — истинная и равновесная концентрации адатомов в адсорбционном слое соответственно.

Заметим, что для достаточно больших концентраций адато­мов вместо поверхностных концентраций следует рассматривать поверхностные активности.

В рассматриваемом случае для равновесия между концен­трацией адатомов в паре и в адсорбционном слое справедливо соотношение (6.7). Таким образом, Δq_а выражает степень пересыщения в системе. Общее изменение энергии Гиббса с учетом уравнений (6.19) и (6.21) запишется в виде

. (6.23)

Радиус критического зародыша находится из условия, опре­деляемого выражением (6.14):

. (6.24)

Подставив уравнение (6.24) в уравнение (6.23), получим выражение для изменения энергии Гиббса при образовании критического зародыша:

(6.25)

Таким образом, изменение свободной энергии образования критического зародыша тем меньше, чем больше движущая сила и чем меньше значение контактного угла θ. Присоедине­ние к критическому зародышу еще одного или нескольких ато­мов приводит к образованию уже устойчивого центра кристал­лизации. При этом энергия Гиббса этого центра кристаллиза­ции уменьшается (рис. 6.13).

Сравнивая выражения для энергии Гиббса образования за­родыша критического размера при гомогенной и гетерогенной кристаллизации, можно записать

Между выражениями (6.15) и (6.25) для радиуса крити­ческого зародыша при гомогенной и гетерогенной кристаллизации существует формальное тождество. Однако, так как гете­рогенное образование зародышей происходит при значениях Δq_об и Δq_а, отличающихся от соответствующих значений, при гомогенном образовании зародышей критические радиусы для обоих типов зародышей различны.

Рис.6.13. Зависимость энергии Гиббса образования зародышей (а) и концентрации зародышей (б) от числа атомов в зародыше: 1 – равновесная концентрация зародышей; 2 – их действительная концентрация

Определим скорость образования зародышей. На поверхности подложки возникают скопления атомов различных размеров: докритического (субзародыши), критического и закритического (сверхзародыши). Скорость образования заро­дышей критического размера для квазистационарного случая определяется как произведение равновесной концентрации кри­тических зародышей на частоту присоединения атомов к зародышуω*:

, (6.26)

где Z — фактор неравновесности (фактор Зельдовича), учиты­вающий отношение концентрации критических зародышей в квазистационарном состоянии к их концентрации в состоянии метастабильного равновесия и градиент концентрации. Для случая двумерного зародыша

(6.27)

и обычно имеет величину от 10^-2до 10^-1.

Для определения величины рассмотрим общуюG системы подложка - адсорбат. Эта энергия складывается из суммы произведений числа агрегатов разных размеров (n_i) на соответствующие энергии образования G_i и из энтропийно­го члена S_см, обусловленного распределением этих агрегатов по n₀ позициям на единичной площадке подложки (плотность узлов адсорбции):

(6.28)

Концентрацию зародышей критического размера в условиях равновесия находим из условия минимума G по их концентра­ции (рис. 6.13, а):

(6.29)

и получаем

(6.30)

Теперь определим ω*. Частота присоединения атомов к за­родышу определяется произведением числа адатомов, примы­кающих к докритическому скоплению атомов (субзародышу) , на частоту диффузионного перескока адсорбиро­ванного атома, где— длина пе­риферии купола:а — расстояние между позициями адсорбции (их число равно n₀); —частота колебаний адсорбированно­го атома (~10¹² . . . 10¹³ с^-1); — энергия активации по­верхностной диффузии:

. (6.31)

Скорость поступления атомов из пара (однородная паровая фаза или молекулярный пучок), называемая плотностью потока j_кон, выражается в кинетической теории газов уравнением (6.12).

Концентрация адатомов свя­зана с плотностью потока пара и временем жизни адатомов выражением . Отсюда следует, что

. (6.32)

Таким образом, скорость образования зародышей критического размера

(6.33)

где А₁ принимается как константа, слабо зависящая от темпе­ратуры и давления.