
- •О.И.Тутынина линейная алгебра
- •210400 «Радиотехника» (профиль «Аудиовизуальная техника»)
- •Пояснительная записка
- •Самостоятельная работа № 6. Тема: Векторное и смешанное произведения векторов
- •Самостоятельная работа № 7. Тема: Способы задания прямой на плоскости
- •Самостоятельная работа № 8. Тема: Способы задания плоскости
- •Самостоятельная работа № 9. Тема: Способы задания прямой в пространстве
- •Самостоятельная работа № 10. Тема: Взаимная ориентация прямой и плоскости
- •Самостоятельная работа № 11. Тема: Преобразования кривых второго порядка
- •Список рекомендуемой литературы
Самостоятельная работа № 8. Тема: Способы задания плоскости
Найти угол между плоскостями х-2у+2z-8=0 и х+z-6=0.
Составить уравнение плоскости, проходящей через точку А(5,-4,6) перпендикулярно оси х.
Найти уравнение плоскости, параллельной плоскости -2+у-4z-5=0 и отстоящей от нее на расстояние, равное 1.
Составить уравнение плоскости, проходящей через точки
 параллельно оси х.
параллельно оси х.
Составить уравнение плоскости, проходящей через начало координат и точку М(3,1,-2) перпендикулярно плоскости х-+2у-3z-2=0.
Найти уравнение плоскости, проходящей через точки А(1,2,0), В(2,1,1) и С(3,0,1).
Найти угол между плоскостями –х+2у-z+1=0 и у+3z-1=0.
Найти уравнение плоскости, проходящей через точки
 параллельно вектору
параллельно вектору
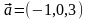 .
.Найти уравнение плоскости, проходящей через начало координат параллельно плоскости 5х-3у+2z-3=0.
Составить уравнение плоскости, проходящей через точки
 параллельно оси z.
параллельно оси z.
Составить уравнение плоскости, проходящей через точку А(5,-4,6) и отсекающую на осях координат равные отрезки.
Найти уравнение плоскости, проходящей через точку М(2,2,-2) параллельно плоскости х-2у-3z=0.
Найти отрезки, отсекаемые плоскостью
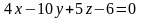 на осях координат.
на осях координат.
Найти расстояние от точки А(4,3,0) до плоскости, проходящей через точки
 .
.
Найти уравнение плоскости, параллельной плоскости -х+у-4z-5=0 и отстоящей от нее на расстояние, равное 6.
Найти расстояние между параллельными плоскостями: 4х+3у-5z-8=0 и 4х+3у-5z+12=0.
Найти уравнение плоскости, проходящей через точку М(1,1,1) параллельно плоскости -2х+у-z+1=0.
Найти уравнение плоскости, проходящей через точки А(3,1,1), В(1,4,1) и С(1,1,6).
Найти уравнение плоскости, проходящей через точки
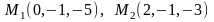 параллельно вектору
параллельно вектору
 .
.Составить уравнение плоскости, проходящей через начало координат и точку М(2,1,-3) перпендикулярно плоскости 2х-у+3z=0.
Самостоятельная работа № 9. Тема: Способы задания прямой в пространстве
Треугольник задан вершинами А(3,1,1), В(1,4,1) и С(1,1,6). Найти уравнение медианы, проведенной из вершины В.
Найти угол между прямыми
 и
и
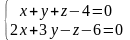 .
.
Найти угол между прямыми
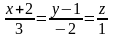 и
и
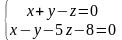 .
.
Найти угол между прямыми
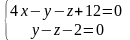 и
и
 .
.
Найти угол между прямыми
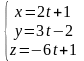 и
и
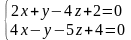 .
.
Найти канонические уравнения прямой, заданной общими уравнениями
 .
.
Даны координаты вершин треугольника А(-1,3,-1), В(2,1,5), С(-4,-2,7). Найти уравнения сторон треугольника.
Даны координаты вершин треугольника А(2,3,1), В(-2,5,6) и С(1,1,4). Найти уравнения сторон треугольника.
Найти канонические уравнения прямой, заданной общими уравнениями
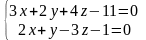 .
.
Найти угол между прямыми
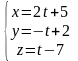 и
и
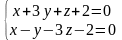 .
.
Написать параметрические уравнения прямой, проходящей через точку М(2,-1,-1) параллельно вектору
 .
.Найти угол между прямой
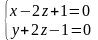 и прямой, проходящей через точку
М(0,1,-1) и начало координат.
и прямой, проходящей через точку
М(0,1,-1) и начало координат.
Написать параметрические уравнения прямой, проходящей через точку М(2,-1,-1) параллельно вектору .
Найти канонические уравнения прямой, заданной общими уравнениями .
Написать каноническое уравнение прямой, проходящей через точку М(-1,2,-2) параллельно прямой
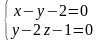 .
.
Найти угол между прямыми
 и
и
 .
.
Найти угол между прямыми и .
