Завдання

Для заданої множини М побудувати бінарні відносини Р и Q і досліджувати їхньої властивості. Відношення Q аналітично й графічно звести в ступені 2,3, а також побудувати транзитивне замикання Q⁺ і транзитивно - рефлексивне замикання Р*. Одержати аналітично і графічно відношення R = Р х Q, знайти для R зворотне відношення й доповнення відносини R.

Таблиця 3

вар	Несуча множина М	Відношення Р	Відношення Q
1	М={1,2,5,7,8}	числа в парі відрізняються більш ніж на три одиниці, і менше число стоїть першим	у парі на першому місці непарне число
2	М={а, b, с, d, f}	«с» або «d» у парі тільки на першому місці	у парі на будь-якому місці одна буква «b»
3	М={2,4,5,6,9}	числа в парі відрізняються не більше, чим на дві одиниці	у парі на будь-якому місці число кратне 3
4	М={а, b, c, е, f}	«а» або «е» у парі тільки на першому місці	у парі на будь-якому місці буква «b»

Продовження таблиці 3

№ вар	Несуча множина М	Відношення Р	Відношення Q
5	М={1,4,6,7,9}	числа відрізняються не менше, ніж на чотири одиниці й більше число стоїть першим	у парі на будь-якому місці парне число
6	М={а, b, з, d, f}	«а» або «b» тільки на другому місці	у парі на будь-якому місці буква «b»
7	М={1,2,3,4,5}	більше на три	парне число тільки на другому місці
8	М={а, b, e, d, f}	«b» або «е» тільки на першому місці	приголосна буква тільки на першому місці
9	М={1,2,3,4,6}	перше число в парі менше на два	непарне число тільки на першому місці
10	М={а, b, e, d, f}	«е» або «d» тільки на другому місці	голосна буква тільки на першому місці
11	М={а, b, з, d, f}	«с» або «d» тільки на першому місці	у парі на будь-якому місці буква «f»
12	М={а, b, з, е, f}	«а» або «f» тільки на першому місці	голосна буква тільки на першому місці
13	M={a,b,e,d,f}	«b» або «d» тільки на другому місці	у парі на будь-якому місці буква «е»
14	М={1,2,3,4,5}	більше на два	парне число тільки на першому місці
15	М={1,2,3,4,6}	менше на три	непарне число тільки на другому місці

Приклад рішення задачі:

Для заданої множини М побудувати бінарні відносини Р и Q і досліджувати їхньої властивості. Відношення Q аналітично й графічно звести в ступені 2,3, а також побудувати транзитивне замикання Q⁺ і транзитивно-рефлексивне замикання Р*. Одержати аналітично й графічно відношення R = Р х Q, знайти для R зворотне відношення й доповнення відносини R.

P=”«с» або «d» тільки на першому місці”

Q=”«a» на будь-якому місці”

Рішення

P={ca, cb, cd, cf, da, db, dc, df}

P	а	b	с	d	f
а	0	0	0	0	0
b	0	0	0	0	0
с	1	1	0	1	1
d	1	1	1	0	1
f	0	0	0	0	0

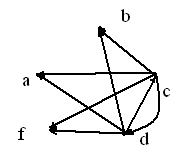
1. Висловлення Р антирефлексивно, тому що на головної диаго­ налі матриці суміжності нулі.

2. Висловлення Р не симетрично, тому що матриця суміжності не симетрична щодо головної діагоналі, а на самої діагоналі розташовані нулію

3.Висловлення Р транзитивно, тому що властивість транзитивності не порушено.

Q	а	b	с	d	f
а	1	1	1	1	1
b	1	0	0	0	0
с	1	0	0	0	0
d	1	0	0	0	0
f	1	0	0	0	0

1. Висловлення Q не рефлексивно, тому що на головній діагоналі матриці суміжності перебувають нулі й одиниці.

2. Висловлення Q симетрично, тому що матриця суміжності симетрична щодо головної діагоналі.

3. Висловлення Q не транзитивно, тому що властивість транзитивності порушена.

2. Відношення Q аналітично й графічно зведемо в ступені

2,3.

Q = {аа, ab, ас, ad, af, ba, ca, da, fa}

Q² = {aa, ab, ac, ad, af,ba,... , ff}

Q³ = { aa, ab, ac, ad, af,ba,... , ff}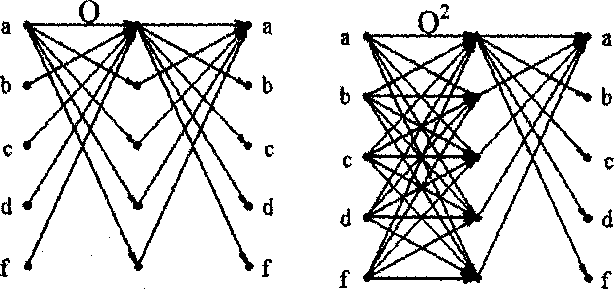

Q² = {aa, ab, ac, ad, af, ba, bb, be, bd, bf, ca, cb, cc, cd, cf, da, ab, dc, dd, df, fa, fb, fc, fd, ff} Q³ = Q²

3, Одержимо аналітично й графічно відношення R = Р х Q,

R = Px Q

Р = {ca, cb, cd, cf, da, db, dc, df}

Q = {aa, ab, ac, ad, af, ba, ca, da, fa}

R = {ca, cb, cc, cd, cf, da, db, dc, dd, df}

4. Знайдемо для R зворотне відношення й доповнення відносини R.

R = {ca, cb, її, cd, cf, da, db, dc, dd, df}

R ^-1 = (ac, be, cc, dc, fc, ad, bd, cd, dd, fd}

_

R = {aa, ab, ac, ad, af, ba, bb, be, bd, bf, fa, ft, fc, fd. ff)

ПРАКТИЧНА РОБОТА №3

Тема: Елементи алгебри логіки (висловлення, складені висловлення, відносини).

Ціль - одержання складених висловлень із заданою таблицею істинності; автоматизація аналізу відносин між парами висловлень.

Завдання

Із трьох простих висловлень р, g, r скласти, використовуючи основні логічні зв'язки, три складові висловлення В, С, D із заданими таблицями істинності, спростити ці висловлення за допомогою еквівалентних перетворень. Установити вид відносин між можливими парами всіх висловлень (А, В, C,D).

Методичні вказівки

1. Побудувати таблицю істинності для висловлення А.

2. Використовуючи таблицю СДНФ, скласти з основних кон'юнкцій складові висловлення В, С, D й, по можливості, спростити їх, використовуючи діаграми Венна.

3. Встановити стосунки між всіма можливими парами складених висловлень (А? В; А? С... С? D)

Таблиця 4

№ варіанта	Номера рядків істинності			Висловлення А
	В	С	D
0	1,5	2,3,6	1,6,2	~(pÚqÙ~r)
1	7,3	7,2,4	7, 6, 2	~( q Ú ~r) Ù p
2	4,6	1,5,8	8,7,3	~(r®q)Ú~p
3	1,5	2,3,6	1,6,2	~(pÙqÚ~r)
4	1,4	1,4,6	2, 7,3	~(pÙ~(q®r))
5	4,6	3,5,7	3,8,4	(~ р Ùq ) Ù ~ r
6	3,7	4,2,8	4,3,5	~(р ® q) Ù ~ r
7	6,. 8	5,3,6	5,4,6	(р Ù ~ q Ú ~ r )
8	5,2	6,3,1	6,5,1	~(( р ® r) Ù ~ q)
9	4,3	7,2,4	7,6,2	~(q Ú ~ r) Ù р
10	1,6	5,8	8,7,3	~(r®q) Ú~p
11	1,8	2,3,6	1,6,2	~р Ú q Ù ~ r
12	2,4	2,5,6	5,6,8	~(q®p ) Ù ~ r
13	3,7	5,3,6	7,6,2	~((р ® r) Ú q)
14	3,5	5,3,6	3,4,6	(~р Úq) Ú~r
15	1,3	2,4,6	2,3,6	~ (~р Ù~qÚr)

Примітка:

Умовні позначки в таблиці:

~ - заперечення (логічне НІ);

Ú - диз'юнкція (логічне АБО);

Ù - кон'юнкция (логічне И);

® - імплікація (якщо..., то...).

Приклад рішення задачі:

Із трьох простих висловлень р, q, r скласти, використовуючи основні логічні зв'язки, три складові висловлення В, С, D із заданими таблицями істинності, спростити ці висловлення, за допомогою еквівалентних перетворень. Установити вид бінарних відносин між всіма можливими парами складених висловлень (А В, С, D). Для висловлення А побудувати перемикальну схему й пояснити її роботу. А = ~ (q Ú ~ r) Ù р® ( q Ù~ r)

В = 7,3

С = 7,2,4

D = 7,6,5,2

Рішення

А = ~ (q Ú ~ r) Ù р® ( q Ù~ r)

В = 7,3

С = 7,2,4

D = 7,6,5,2