5.Методичні вказівки до виконання контрольної роботи
Завдання 1
Відомо, що при вкладанні капіталу в захід А із 100 випадків прибуток 1500 гривень було отримано 50 разів, прибуток 760 гривень - 15, а прибуток 1000 гривень - 35разів, а при вкладанні капіталу в захід Б із 75 випадків прибуток 700 гривень було отримано 40 разів, прибуток 1200 - 20 і прибуток 1700 - 15 разів. Потрібно визначити варіант вкладання капіталу за допомогою показників математичного сподівання, дисперсії, середньоквадратичного відхилення і коефіцієнта варіації.
Розв’язок.
Для того, щоб виконати усі необхідні розрахунки і зробити відповідні висновки потрібно спочатку розрахувати ймовірність виникнення кожної суми прибутку. Так, для заходу А , ймовірність виникнення прибутку 1500 гривень визначається як 50/100=0,5 ; прибутку 760 гривень 15/100=0,15 ; прибутку 1000 гривень 35/100=0,35. Для заходу Б ймовірність виникнення прибутку 700 гривень визначається як 40/75=0,53 ; прибутку 1200 гривень 20/75=0,27 ; прибутку 1700 гривень 15/75=0,2. Тут потрібно пам’ятати, що ймовірність визначається в долях одиниці і сума альтернативних ймовірностей за кожним заходом повинна дорівнювати одиниці.
Результати зведемо в табл.8.
Таблиця 8
Вихідні дані для розрахунків
-
Прибуток
Ймовіір-ність
Прибуток
Ймовір-ність
Прибуток
Ймовір-ність
Захід А
1500
0,5
760
0,15
100
0,35
Захід Б
700
0,53
1200
0,27
1700
0,2
Математичне сподівання (М) знаходимо за формулою:
,
(1)
де Xi- значення показника в і-тій ситуації;
Рі-ймовіірність виникнення Хі.
Дисперсію (2) за формулою:
2
=
.
(2)
Середньоквадратичне відхилення () за формулою:
=(2). (3)
Коефіцієнт варіації (cv) за формулою:
cv=/М. (4)
Для зручності розрахунків побудуємо табл.9.
Таблиця 9
Розрахунок коефіцієнта варіації для заходів А і Б
-
Показник
Захід А
Захід Б
Математичне сподівання
1500*0,5+760*0,15+
+1000*0,35=1214
700*0,53+1200*0,27+
+1700*0,2=1035
Дисперсія
(1500-1214)2*0,5+(760-
-1214)2 *0,15+(1000-
-1214)2 *0,35=87844
(700-1035)2*0,53+(1200-
-1035)2 *0,27+(1700-
-1035)2 *0,2=155275
Середнє квадратичне відхилення
296,4
394,05
Коефіцієнт варіації
296.4/1214=0,24
394,05/1035=0,38
При впровадженні заходу А сподіваний дохід більше, ніж при впровадженні заходу Б, так як 1035<1214, і ступінь ризику також менша, так як 296,4<394,05. Для того, щоб зробити вибір потрібно розрахувати коефіцієнт варіації, тобто обчислити кількість ризику на одиницю доходу. При впровадженні заходу Б кількість ризику на одиницю доходу буде більше (0,24< 0,38), а значить потрібно обрати проект А.
Завдання 2
Маємо два інвестиційні проекти. Норма прибутку по кожному з них залежить від економічної ситуації на ринку. Припустимо, що на ринку можуть виникнути лише дві ситуації: ситуація А з ймовірністю 0,2 і ситуація Б - 0,8.
Різні проекти неоднаково реагують на економічні ситуації: прибуток першого проекту за обставин А зростає на 5%; за обставин Б - на 1,25%; прибуток другого проекту за обставин А падає на 1%; за обставин Б зростає на 2,75%.
Припустимо, що інвестор бере гроші в борг під відсоток, що дорівнює 1,5%. Який проект потрібно впровадити з точки зору ризику банкрутства?
Розв’язок.
Спочатку розрахуємо сподівані норми прибутку за кожним проектом, використовуючи формулою (1):
М(1)=+5%*0,2+1,2%*0,8=2%;
М(2)=-1%*0,2+2,75%*0,8=2%.
Обчислимо дисперсії ефективності цих проектів за формулою (2):
2 (1)=(5-2)2 *0,2+(1,25-2)2 *0,8=2,25;
2 (2)=(-1-2)2 *0,2+(2,75-2)2 *0,8=2,25.
Тепер можна розрахувати ризик цих проектів за формулою (3):
(1)=2,25=1,5;
(2)=2,25=1,5.
Можна зробити висновок, що сподівана прибутковість і ризик обох проектів однакові. Відсоток, під який взято гроші в борг, нижчий, ніж сподівана прибутковість проектів (1,5%<2,0%), тому можна вважати, що інвестор вчинив розсудливо.
Висновок щодо вибору одного із двох проектів потрібно зробити з точки зору ризику банкрутства. Для цього розрахуємо виграш інвестора, тобто той процент який він отримає після того як розрахується за користування позикою. Для зручності розрахунків побудуємо табл.10.
Таблиця 10
Виграш інвестора
-
Ситуація А
Ситуація Б
Проект 1
5%-1,5%=3,5%
1,25%-1,5%=-0,25%
Проект 2
-1%-1,5%=-2,5%
2,75%-1,5%=1,25%
Ймовірність виникнення ситуації
0,2
0,8
Як си бачимо із табл.10 перший проект збанкрутує коли відбудеться ситуація Б, а другий проект збанкрутує коли відбудеться ситуація А. Ситуації А і Б мають різну ймовірність, тому з точки зору ризику банкрутства рішення інвестора полягає у виборі такого проекту ймовірність банкрутства якого буде меншою. Перший проект збанкрутує з ймовірністю 0,8, а другий - 0,2, тобто, треба обрати для впровадження другий проект.
Завдання 3
Підприємству потрібно визначити яку кількість продукції потрібно випустити, щоб отримати найбільший прибуток. Рішення залежить від ситуації на ринку, тобто, від конкретної кількості споживачів. Конкретна кількість споживачів наперед невідома і може бути трьох варіантів: S1,S2 i S3. Є можливими чотири варіанти випуску продукції підприємством: А1,А2,А3 і А4. Кожній парі, що залежить від стану середовища - Sj та варіанту рішення - Ai відповідає значення функціоналу оцінювання - V(Ai,Sj), що характеризує результат дій (табл.11).
Таблиця 11
Прибуток від реалізації
-
Варіанти рішень
Варіанти станів середовища
S1
S2
S3
А1
2,5
3,5
4,0
А2
1,5
2,0
3,5
А3
3,0
8,0
2,5
А4
7,5
1,5
3,5
Ймовірність стану середовища
0,25
0,55
0,20
Потрібно знайти оптимальну альтернативу випуску продукції з точки зору максимізації прибутку за допомогою критеріїв Байєса за умов відомих ймовірностей станів , Лапласа, Вальда, Севіджа за умов повної невизначеності і Гурвіца із коефіцієнтом оптимізму 0,6
Розв’язок.
Оптимальна альтернатива за критерієм Байєса знаходиться за формулами:
Для F+ Аі*=max i { V(Ai,Sj)*Pj} ; (5)
Для F- Аі*=min i { V(Ai,Sj)*Pj} . (6)
Ми знаходимо оптимальну альтернативу випуску продукції з точки зору максимізації прибутків, тобто функціонал оцінювання має позитивний інгредієнт - F+ і будемо використовувати відповідні формули. Всі розрахунки показані в табл.12
Таблиця 12
Вибір оптимального рішення за критерієм Байєса
-
Варі-анти рі-
Варіанти станів середовища
V(Ai,Sj)*Pj
max i { V(Ai,Sj)*Pj}
шень
S1
S2
S3
А1
2,5
3,5
4,0
2,5*0,25+3,5*0,55+4,0*0,2=3,350
А2
1,5
2,0
3,5
1,5*0,25+2,0*0,55+3,5*0,2=2,175
А3
3,0
8,0
2,5
3,0*0,25+8,0*0,55+2,5*0,2=5,650
А3*
А4
7,5
1,5
3,5
7,5*0,25+1,5*0,55+3,5*0,2=3,400
За критерієм Байєса оптимальним буде альтернативне рішення А3.
Критерій Лапласа характеризується невідомим розподілом ймовірностей на множині станів середовища і базується на принципі «недостатнього обґрунтування», який означає: якщо немає даних для того, щоб вважати один із станів середовища більш ймовірним, то ймовірності станів середовища треба вважати рівними. Оптимальна альтернатива за критерієм Лапласа знаходиться за формулами:
Для
F+
Аі*=max i
{1/n
V(Ai,Sj)}
; (7)
Для F- Аі*=min i {1/n V(Ai,Sj)}. (8)
Всі розрахунки в табл.13.
Таблиця 13
Вибір оптимального рішення за критерієм Лапласа
-
Варі-анти рі-шень
Варіанти станів середовища
1/n V(Ai,Sj)
max i { 1/n V(Ai,Sj)}
S1
S2
S3
А1
2,5
3,5
4,0
1/3*(2,5+3,5+ 4,0)=3,333
А2
1,5
2,0
3,5
1/3*(1,5+2,0+ 3,5)=2,333
А3
3,0
8,0
2,5
1/3*(3,0+8,0+ 2,5)=4,500
А3*
А4
7,5
1,5
3,5
1/3*(7,5+1,5+ 3,5)=4,167
За критерієм Лапласа оптимальним буде альтернативне рішення А3.
Критерій Вальда вважається самам обережним із критеріїв. Оптимальне альтернативне рішення за критерієм Вальда знаходиться за формулами:
Для F+ Аі*=max i min j { V(Ai,Sj)} ; (9)
Для F- Аі*=min i max j { V(Ai,Sj)} . (10)
Всі розрахунки в табл.14.
Таблиця 14
Вибір оптимального рішення за критерієм Вальда
-
Варі-анти рі-шень
Варіанти станів середовища
min j
{ V(Ai,Sj)}
max i min j { V(Ai,Sj)}
S1
S2
S3
А1
2,5
3,5
4,0
2,5
А1*
А2
1,5
2,0
3,5
1,5
А3
3,0
8,0
2,5
2,5
А3*
А4
7,5
1,5
3,5
1,5
За критерієм Вальда оптимальними будуть альтернативні рішення А1 і А3, які вважаються еквівалентними, тобто мають однакові переваги для виконання.
Для того, щоб застосувати критерій Севіджа, потрібно побудувати матрицю ризику, як лінійне перетворення функціоналу оцінювання.
Для побудови матриці ризику використовують такі формули:
Для F+ Rіj*=max i { V(Ai,Sj)} - V(Ai,Sj) ; (11)
Для F- Rij*= V(Ai,Sj) - min i { V(Ai,Sj)} . (12)
Матрицю ризику побудуємо в табл.15.
Таблиця 15
Побудова матриці ризику
-
Варіанти
Матриця прибутків (V(Ai,Sj))
Матриця ризику (Rij)
рішень
Варіанти станів середовища
Варіанти станів середовища
S1
S2
S3
S1
S2
S3
А1
2,5
3,5
4,0
7,5-2,5=5,0
8,0-3,5=4,5
4,0-4,0=0
А2
1,5
2,0
3,5
7,5-1,5=6,0
8,0-2,0=6,0
4,0-3,5=0,5
А3
3,0
8,0
2,5
7,5-3,0=4,5
8,0-8,0=0
4,0-2,5=1,5
А4
7,5
1,5
3,5
7,5-7,5=0
8,0-1,5=6,5
4,0-3,5=0,5
Тепер можна застосувати критерій Севіджа до матриці ризику за формулою:
Аі*=min i max j { Rij} . (13)
Всі розрахунки в табл.16.
Таблиця 16
Вибір оптимального рішення за критерієм Севіджа
-
Варі-анти рі-шень
Варіанти станів середовища
max j { Rij}
min i max j { Rij}
S1
S2
S3
А1
5,0
4,5
0
5,0
А2
6,0
6,0
0,5
6,0
А3
4,5
0
1,5
4,5
А3*
А4
0
6,5
0,5
6,5
За критерієм Севіджа оптимальним буде альтернативне рішення А3.
Критерій Гурвіца дозволяє встановити баланс між випадками крайнього оптимізму і випадками крайнього песимізму за допомогою коефіцієнта оптимізму . визначається від нуля до одиниці і показує ступінь схильностей людини, що приймає рішення, до оптимізму або песимізму. Якщо =1, то це свідчить про крайній оптимізм, якщо =0 - крайній песимізм. За умов задачі =0,6.
Оптимальна альтернатива за критерієм Гурвіца знаходиться за формулами:
Для F+ Аі*=maxi{*maxj{V(Ai,Sj)}+(1-)minj{V(Ai,Sj)}}; (14)
Для F- Аі*=mini{(1-)*maxj{V(Ai,Sj)}+minj{V(Ai,Sj)}}. (15)
Всі розрахунки в табл.17.
Таблиця 17
Вибір оптимального рішення за критерієм Гурвіца
-
Варі-анти
Варіанти станів сере-довища
maxj {V(Ai,Sj)}
minj {V(Ai,Sj)}
*maxj{V(Ai,Sj)}+(1-)minj{V(Ai,Sj)}
maxi{*maxj{V(Ai,Sj)}+(1-)minj{V(Ai,Sj)}}
рі-шень
S1
S2
S3
А1
2,5
3,5
4,0
4,0
2,5
4,0*0,6+
+2,5*0,4=3,4
А2
1,5
2,0
3,5
3,5
1,5
3,5*0,6+
+1,5*0,4=2,7
А3
3,0
8,0
2,5
8,0
2,5
8,0*0,6+
+2,5*0,4=5,8
А3
А4
7,5
1,5
3,5
7,5
1,5
7,5*0,6+
+1,5*0,4=5,1
Оптимальним рішенням за критерієм Гурвіца буде альтернативне рішення А3.
Завдання 4.
Підприємство має тимчасово вільні кошти 10000 грн. і вирішує питання про їх використання. Можна вкласти гроші в деякий інвестиційний проект. У випадку невдачі підприємство втрачає свої гроші, а у випадку успіху через рік отримує 40000 грн. Альтернативний варіант - вкласти гроші в банк під 9% річних без ризику. У випадку вкладання кошт в інвестиційний проект спеціаліст з маркетингу вважає, що ймовірність успіху - 0,3.
Щоб прийняти рішення щодо використання підприємством грошей потрібно врахувати думку директора і бухгалтера. Відомості про корисносність різних сум доходів директора і бухгалтера в табл.18.
Таблиця 18
Корисність різних сум доходів директора і бухгалтера підприємства
Корисність |
Доход, тис. грн. |
||||
з точки зору |
0 |
10 |
20 |
30 |
40 |
директора |
0 |
10 |
25 |
50 |
100 |
бухгалтера |
0 |
45 |
75 |
90 |
100 |
Потрібно : визначити варіант вкладання кошт за допомогою критерію сподіваного доходу ; побудувати два графіки корисності і визначити за ними відношення до ризику обох спеціалістів; визначити корисність доходів для кожного спеціаліста і що порадить кожен з них за правилом сподіваної корисності.
Розв’язок.
Спочатку розрахуємо сподівані доходи для двох варіантів вкладання кошт. Всі розрахунки в табл.19.
Таблиця 19
Розрахунок сподіваного доходу
-
Можливі
Можливі рішення
Ймовірність
результати
Інвестиції
Банк
Успіх
40000
10900
0,3
Невдача
0
10900
0,7
Сподіваний доход
12000
10900
Дисперсія
151400000
0
Ризик
12304,5
0
Коефіцієнт варіації
1,03
0
Дисперсія за умов впровадження інвестиційного проекту складатиме 151400000 (2 = (40000-12000)2 *0,3+(0-12000)2 *0,7 = 151400000), а ризик 12304,5 ( =151400000=12304,5), а при вкладанні грошей в банк ризик відсутній. За сподіваним доходом потрібно обрати варіант вкладання кошт в інвестиційний проект, але, якщо врахувати ризик і розрахувати коефіцієнт варіації, то більш привабливим буде варіант вкладання кошт в банк.
Намалюємо два графіки корисності доходів, відповідно, бухгалтера (рис.1) і директора (рис.2) , користуючись шкалою корисностей (табл.18).
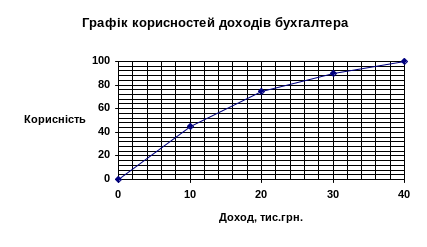
Рисунок 1
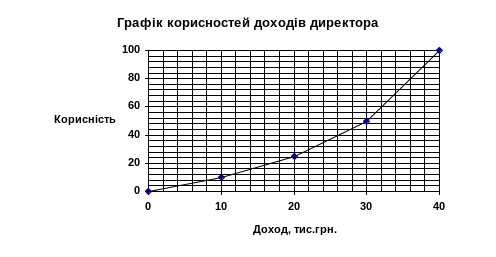
Рисунок 2
За графіками можна зробити висновок, що директор підприємства схильний до ризику, так як його графік корисності доходів вогнутий. Це також підтверджується умовою схильності до ризику, яка визначається формулою:
U( M(x) ) < M ( U(x) ), (16)
де U( M(x) ) - корисність сподіваного результату;
M ( U(x) ) - сподівана корисність результатів.
Бухгалтер за графіком не схильний до ризику, так як його графік - випуклий. Це підтверджується умовою несхильності до ризику, яка визначається формулою:
U( M(x) ) > M ( U(x) ). (17)
Тепер розрахуємо сподівану корисність доходів для директора і бухгалтера. Для чого потрібно перетворити шкалу доходів на шкалу корисностей для бухгалтера і директора, користуючись відповідними графіками.
Сподівана корисність розраховується за формулою:
М
(U(x))
=
, (18)
де U(xi) - корисність хі;
Рі - ймовірність хі.
Розрахунки сподіваних корисностей бухгалтера і директора, відповідно, в табл.20 і табл.21.
Таблиця 20
Розрахунок сподіваної корисності бухгалтера
-
Можливі
Можливі рішення
Ймовірність
результати
Інвестиції
Банк
Успіх
100
48
0,3
Невдача
0
48
0,7
Сподівана корисність
100*0,3+0*0,7=30
48
Таблиця 21
Розрахунок сподіваної корисності директора
-
Можливі
Можливі рішення
Ймовірність
результати
Інвестиції
Банк
Успіх
100
12
0,3
Невдача
0
12
0,7
Сподівана корисність
100*0,3+0*0,7=30
12
За сподіваною корисністю бухгалтер запропонує вкласти гроші в банк без ризику (12<30) , а директор - в інвестиційний проект (48>30) .
Завдання 5.
Виробник звернувся у відділ маркетингу для того, щоб з’ясувати сподіваний попит на товар. Попит на товар за попередніми розрахунками може бути : 1000;2000;3000 і 4000 одиниць товару. Відхилення від цих рівнів призводить до додаткових витрат або через перевищення пропозиції над попитом - 3 грн., або через неповне задоволення попиту – 2 грн. за одиницю. Доход від виробництва товару – 10 грн. за одиницю.
Потрібно побудувати таблицю доходів від реалізації відповідно тих ситуацій, що можуть відбутись на ринку і тих рішень, що ми можемо прийняти.
Розв’язок.
Доход від реалізації розраховується, як доход від виробництва мінус всі відомі витрати, що пов’язані із реалізацією.
Припустимо, що на ринку відбудеться попит на 1000 одиниць товару і ми виробимо 1000 одиниць товару. Доход від виробництва складе 10000 грн.(1000*10=10000). А збитки відповідно тих, що вказані в умові відсутні. Тоді доход від реалізації буде 10000 грн. (10000-0=10000).
Припустимо, що на ринку відбудеться попит на 1000 одиниць товару, а ми випустимо 2000 одиниць товару. Доход від виробництва складе 10000 грн. (1000*10=10000), так як ми зможемо реалізувати тільки 1000 одиниць товару, що визначається попитом. Перевищення пропозиції над попитом 1000 одиниць товару (2000-1000=1000). А збитки через перевищення пропозиції над попитом будуть 3000 грн. (1000*3,00=3000). Тоді доход від реалізації буде 7000 грн. (10000-3000=7000).
Припустимо, що на ринку відбудеться попит на 2000 одиниць товару, а ми випустимо 1000 одиниць товару. Доход від виробництва складе 10000 грн. (1000*10=10000), так як ми зможемо реалізувати тільки 1000 одиниць товару, що визначається кількістю випущеної продукції. Незадоволення попиту - 1000 одиниць товару (2000-1000=1000). А збитки через незадоволення попитом будуть 2000 грн. (1000*2,00=3000). Тоді доход від реалізації буде 8000 грн. (10000-2000=8000).
Шукана таблиця доходів набуде такого вигляду:
Таблиця 22
Доход від реалізації товарів, тис. грн.
-
Кількість вироблених
Сподіваний попит, що може статись на ринку, од.
одиниць товару
1000
2000
3000
4000
1000
10000
8000
6000
4000
2000
7000
20000
18000
16000
3000
4000
17000
30000
28000
4000
1000
14000
27000
40000
Завдання 6.
Для деякої компанія відомі такі показники: чутливість компанії до ринку =1,1%; безризикова ставка krf =10%; середня доходність ринку k m=15%. Компанія збирається впроваджувати новий проект, чутливість до ринку нового проекту н =1,5. Потрібно розрахувати необхідну доходність компанії з урахуванням нового проекту і сподівану доходність нового проекту, якщо 70% капіталу компанія залишає під існуючі проекти і 30% вкладає в новий проект. За розрахованими даними потрібно побудувати лінію надійності ринку.
Розв’язок.
Лінія надійності ринку виражає залежність між ризиком інвестиційного проекту і його необхідною доходністю за формулою:
k s = krf + (k m - krf )* . (19)
Якщо компанія не використовує позичкові кошти, то інвестори будуть готові складувати кошти в її «середньризикові проекти» , якщо сподіваються отримати доходи на рівні не нижче 15,5% (10%+(15%-10%)*1,1=15,5%). «Середньоризикові проекти» - це такі проекти які вже реалізовані і на основі яких розраховано значення =1,1%.
Якщо ми впроваджуємо новий проект, ризик якого відрізняється від середнього, тобто н =1,5 , то даний проект змінює - коефіцієнт компанії, а, відповідно, і необхідну прибутковість капіталу. Так як будь-якого портфеля інвестицій визначається як середньозважена величина -коефіцієнтів проектів, що його складають, то ризик портфеля з урахуванням нового проекту збільшиться і складе величину 1,22 (0,7*1,1+0,3*1,5=1,22).
Це зростання ризику компанії може відштовхнути майбутніх інвесторів, якщо не буде компенсовано зростанням сподіваної доходності. Сподівана доходність повинна збільшитись до величини 16,1% (10%+(15%-10%)*1,22=16,1%).
Таким чином, щоб залучити інвесторів, сподівана доходність компанії після впровадження нового проекту повинна зрости від 15,5% до 16,1%.
Якщо доходність існуючих інвестиційних проектів повинна складати 15,5%, доходність компанії з урахуванням нового проекту 16,1%, то сподівана доходність нового проекту повинна бути не нижче 17,5% ( 0,7*15,5%+0,3* k% =16,1% ; k= 17,5% або 10%+(15%-10%)*1,5=17,5%).
Так, якщо компанія приймає новий проект, її корпоративний ризик, що виражається -коефіцієнтом, зростає від 1,1 до 1,22, доходність від 15,5% до 16,1%, а доходність нового проекту повинна бути не менше 17,5%.
Графічно цей взаємозв’язок зображено на рис.3.
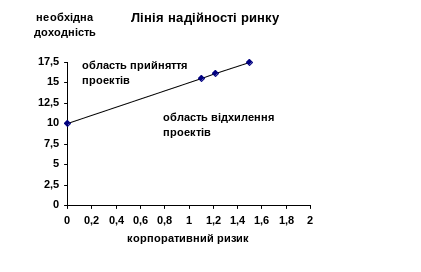
Рисунок 3