1.1.6 Перевірка гіпотези про вид закону розподілу результатів

спостережень

Якщо закон розподілу результатів спостережень невідомий то часто на основі певних міркувань висувають гіпотезу: результати спостережень розподілені за законом А, наприклад, за нормальним.

Перевірка гіпотези про вид закону розподілу проводити методами статистичної перевірки статистичних гіпотез. Статистичною називають гіпотезу про вид невідомого розподілу чи про параметри відомих розподілів. Висунуту гіпотезу називають нульовою (основною) гіпотезою. Якщо висунута гіпотеза буде відкинута, то має місце протилежна гіпотеза. Протилежна гіпотеза називається конкуруючою (альтернативною).

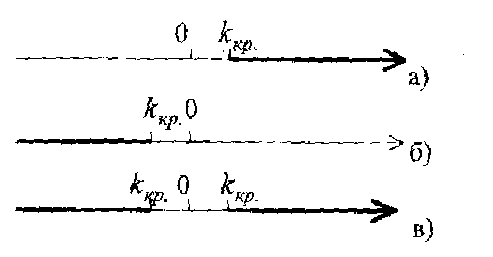
Рисунок 1 - Критичні області:

а) правостороння критична область ,

б) лівостороння критична область ,

в) двостороння критична область .

Для перевірки нульової гіпотези використовують спеціально підібрану випадкову величину, позначимо її через К, розподіл якої відомий. Величину К називають статистичним критерієм, або просто критерієм. Після вибору певного критерію множину всіх його можливих

значень розбивають на дві підмножини:

- одна з них містить значення критерію, при яких нульова гіпотеза приймається,

- друга містить значення критерію, при яких ця гіпотеза відкидається.

Першу область називають областю прийняття гіпотези, другу-критичною областю.

Критерій К - одномірна випадкова величина. Таким чином критична область та області прийняття гіпотези є інтервалами і відділені одна від одної границями, які називають критичними точками k_кр .

Для її знаходження задаються достатньо малою імовірністю - рівнем значимості . Потім знаходять критичні (якщо критична область двостороння) чи критичну точку, виходячи з вимоги, щоб при умові справедливості нульової гіпотези ймовірність того, що критерій X прийме значення, яке належите критичній області, було рівне прийнятому рівню значимості. Для кожного критерію побудовані відповідні таблиці, за якими на практиці і знаходять критичні точки, які відповідають дим вимогам. Якщо критичні точки знайдені, тоді далі розраховують , за результатами вибірки значення критерію і, якщо виявиться, що розраховане значення критерію потрапляє в критичну область, то нульову гіпотезу відкидають, якщо в область прийняття гіпотези, то відкидати нульову гіпотезу не має підстав. Однак, якщо нульова гіпотеза не відкинута, це не значить , що вона доведена. Більш правильно буде сказати, що дані спостережень узгоджуються з нульовою гіпотезою, тобто немає підстав її відкидати.

1.1.7 Методи перевірки гіпотез про вид закону розподілу

Перевірка гіпотези про закон розподілу проводиться таким же чином, як і перевірка гіпотеза про параметри розподілу, тобто на основі критерію перевірки про вид невідомого розподілу, який називають критерієм узгодженості.

Існує кілька критеріїв: ² Пірсона чи ² Мізеса - Смірнова та інші. Розглянемо спочатку критерій Пірсона, який може бути використаний не лише для перевірки нормальності розподілу, але й для перевірки гіпотез про інші види розподілів.