1.1.9 Статистична характеристика якості продукції

Нехай деяка технологічна система здійснює безперервний випуск продукції, наприклад цех гумових виробів для високовольтних повітряних вимикачів виготовляє гумові ущільнення. Якість продукції, що випускається,

Таблиця 5 - Квантілі u_р нормованого нормального розподілу для різних Р

р	uр	р	uр	р	uр	p	uр
0,50	0,000000	0,70	0,524401	0,90	1,281552	0,9830	2,120072
0,51	0,025069	0,71	0,553385	0,91	1,340755	0,984	2,144411
0,52	0,050154	0,72	0,582842	0,92	1,405072	0,985	2,170090
0,53	0,075270	0,73	0,612813	0,93	1,475791	0,986	2,197286
0,54	0,100434	0,74	0,643345	0,94	1,554774	0,987	2,226212
0,55	0,125661	0,75	0,674490	0,95	1,644854	0,988	2,257129
0,56	0,160969	0,76	0,706303	0,96	1,750686	0,989	2,290368
0,57	0,176374	0,77	0,738847	0,97	1,880794	0,990	2,326348
0,58	0,201893	0,78	0,772193	0,971	1,895698	0,991	2,365618
0,59	0,227545	0,79	0,806421	0,972	1,911036	0,992	2,408916
0,60	0,253347	0,80	0,841621	0,973	1,926837	0,993	2,457263
0,61	0,279319	0,81	0,877896	0,974	1,943134	0,994	2,512114
0,62	0,305481	0,82	0,915365	0,975	1,959964	0,995	2,575829
0,63	0,331853	0,83	0,954165	0,976	1,977368	0,996	2,652070
0,64	0,358459	0,84	0,994458	0,977	1,995393	0,997	2,747781
0,65	0,385320	0,85	1,036433	0,978	2,014091	0,998	2,878162
0,66	0,412463	0,86	1,080319	0,979	2,033520	0,99865	3,002445
0,67	0,439913	0,87	1,126391	0,980	2,053749	0,999	3,090232
0,68	0,467699	0,88	1,174987	0,981	2,074855	-	-
0,69	0,495850	0,89	1,226528	0,982	2,096927	-	-

оцінюється значенням вимірюваного показника якості (наприклад, розмір зовнішнього діаметру ущільнення під ізолятор опори камери повітряного вимикача - 202  0,5 мм), позначимо його y. Нехай номінальне, тобто необхідне значення показника якості, є у_о (наприклад, 202 мм). Працююча технологічна система володіє природною похибкою виготовлення продукції. Під похибкою виготовлення y розуміємо відхилення фактичного значення показника якості у від номіналу y₀:

y = y - y₀. (39)

Технічні вимоги до якості продукції визначаються полем допуску

 = T_в + T_н, (40)

де  - поле допуску; T_в - верхнє припустиме відхилення показника якості у від необхідного номіналу y_o (в нашому випадку це + 0,5 мм); T_н - нижнє припустиме відхилення показника T_н якості у від необхідного номіналу y_o (в нашому випадку це - 0,5 мм).

У загальному випадку може бути, що

T_в  T_н (41)

Продукція, що випускається, вважається придатною, якщо вимірюване значення показника якості y лежить в межах (y₀ + T_в; y₀ - T_н). Якщо значення показника якості виходить за межі технологічного допуску, продукція вважається непридатною (брак). Брак є наслідком похибок роботи технологічної системи.

Похибка технологічної системи має дві складові: випадкову і систематичну.

Випадкова похибка обумовлена впливом на технологічний процес випадкових явищ (наприклад, неоднорідність сировини, зміни навколишнього середовища, механічні вібрації і т.д.).

Оскільки факторів, що породжують випадкову похибку, звичайно буває багато і серед них важко виділити домінуючий, то на підставі центральної граничної теореми теорії імовірностей можна вважати, що розподіл випадкової похибки відповідає нормальному закону з нульовим математичним очікуванням і деякою дисперсією σ^2. Величина (σ² характеризує точність роботи технологічної системи.

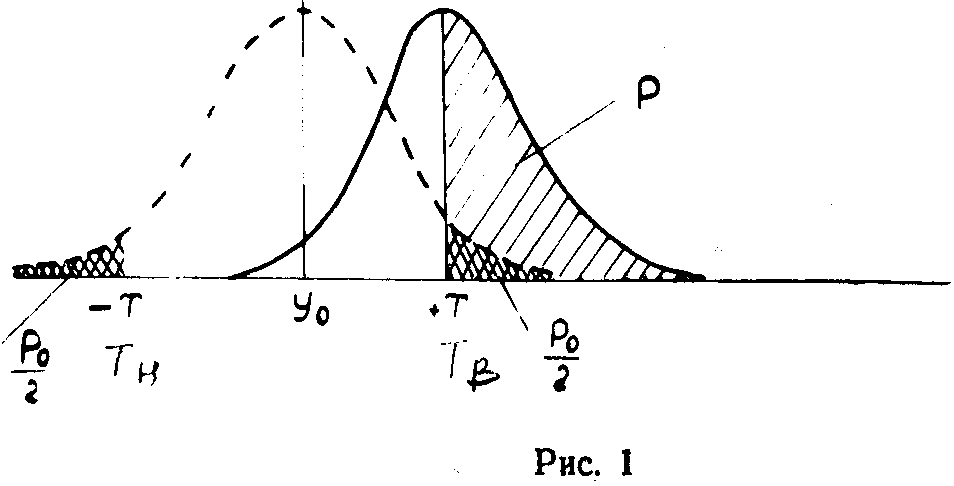
Рисунок 3 - Нормальний закон розподілу

Систематична похибка зв'язана з виникненням у технологічному процесі стійких і, як правило, зростаючих відхилень, що збільшуються внаслідок дії таких факторів, як поступовий знос обладнання, старіння каталізатора, забруднення технологічного обладнання і т.п. Величина систематичної похибки визначає положення центра об'єднання (математичного чекання) випадкової похибки на осі значень показника якості y.

Зростання будь-якої складової похибки технологічної системи призводить до зростання частки браку [1,2,3]. Пояснимо це графічно.

На рисунку 3 зображена вісь значень показника якості y, на якій відзначені значення номіналу y₀ і границі допуску (у припущенні T_в = T_н). Якщо технологічна система налаштована на необхідний номінал y₀ і буде відсутня систематична похибка, то математичне чекання випадкової похибки збігається з номіналом y₀ і крива щільності розподілу випадкової похибки розміщена так, як показано пунктиром. Закреслені частини площі під кривою відповідають імовірності ₀ того, що фактичне значення показника якості у виявиться за межами допуску.

Тоді при даній точності технологічної системи (² і відсутності систематичної похибки відсоток браку в продукції, що випускається дорівнює 100%. З появою систематичної похибки математичне очікування випадкової похибки зсувається відносно номінального значення y₀.

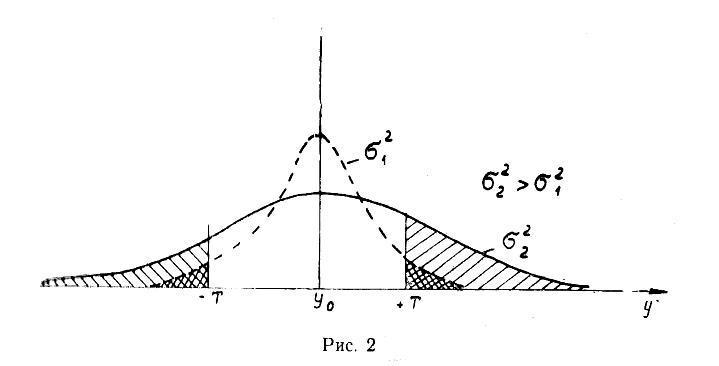
Рисунок 4 - Зростання частини браку при погіршенні точності роботи

технологічної системи

У цьому випадку імовірність  виходу значень показника якості y за границі допуску визначається заштрихованою частиною площі під суцільною кривою. Ясно, що ₀ і, виходить, частка браку зростає з появою статистичної погрішності, хоча точність роботи (²) технологічної системи може бути незмінною. Рисунок 4 аналогічним чином показує зростання частини браку при погіршенні точності роботи технологічної системи (зростання ²).

Технологічний процес "йде" стабільно, якщо не виникає систематичної похибки і не змінюється величина випадкової похибки . Визначимо частину браку, що випускає стабільно працююча технологічна система при даному співвідношенні між полем допуску  і величиною ². Нехай T_в = T_н = T; тоді при існуючій точності роботи технологічної системи ² імовірність появи браку дорівнює

(42)

При стабільному процесі випадкова величина має нормальний розподіл з нульовим математичним очікуванням і одиничною дисперсією. Тоді

(43)

де — табличне значення функції розподілу нормованої нормальної випадкової величини при

Отже,

(44)

де = - нормована функція Лапласа (значення наведені в додатку)

, (45)

де t= .

Величина q·100% є дуже важливою характеристикою статистичного контролю якості, тому що вона характеризує відсоток браку, що утвориться в ході стабільного технологічного процесу.