Раздел 1

1. А	6. А	11. А	16. А	21. А
2. В	7. В	12. В	17. С	22. С
3. С	8. С	13. С	18. В	23. В
4. D	9. D	14. D	19. D	24. D
5. E	10.Е	15. Е	20. Е	25. А

Раздел 2

1. В	6. А	11. А	16. В	21. С
2. Е	7. В	12. В	17. С	22. В
3. А	8. С	13. Е	18. D	23. D
4. В	9. D	14. D	19. А	24. А
5. E	10.С	15. А	20. Е	25. Е

Раздел 3

1. А

2. А

3. А

4. А

5. С

Теоретические вопросы

1 Если тело в форме параллелепипеда, то объем вычисляется по формуле:

2 Укажите основное свойство двойных интегралов:

3 Укажите основное свойство двойных интегралов:

4 Если плотность тела , масса вычисляется по формуле:

5 Если тело задано, укажите формулу приведения к повторным интегралам тройного интеграла :

6 Если плотность пластинки , масса вычисляется по формуле:

7 Объем цилиндрического тела Т, ограниченного сверху непрерывной поверхностью и в области , снизу областью плоскости Оху, сбоку цилиндрической поверхностью с образующими, параллельными оси Оz вычисляется с помощью двойного интеграла по формуле :

8 Объем тела вычисляется по формуле:

9 Если область , функции и непрерывные на , двойной интеграл приводится к повторным интегралам:

10 Площадь области вычисляется по формуле:

11 Указать в двойных интегралах формулу перехода к полярным координатам: .

12 Площадь области в полярных координатах вычисляется по формуле:

Вопросы.

1Какой ряд называется рядом Тейлора функции f (x) в окрестности точки x₀.

1. 

2 Укажите формулу Тейлора функции f (x) в окрестности точки x₀. ( r_n(x) - остаточный член формулы Тейлора)

1. f (x) = 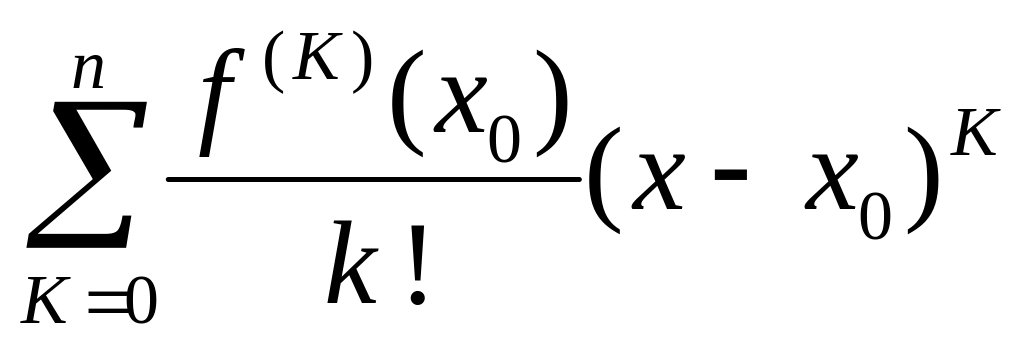+r_n(x)

3 Укажите достаточное условие сходимости ряда Тейлора бесконечно дифференцируемой функции f (x) на некотором интервале к функции f (x) ( r_n(x) - остаточный член формулы Тейлора, s_n(x) - n-я частичная сумма ряда Тейлора)

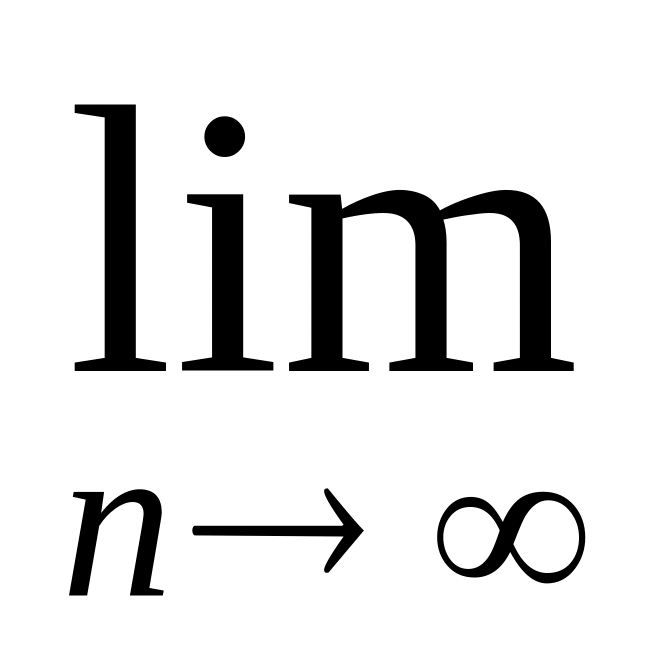1. r_n(x)=0

1. Функции нескольких переменных. (Теоретические вопросы).

1. 01. Для функции Z=f(x, y) частная производная по x в точке M₀ (x₀, y₀) определится формулой

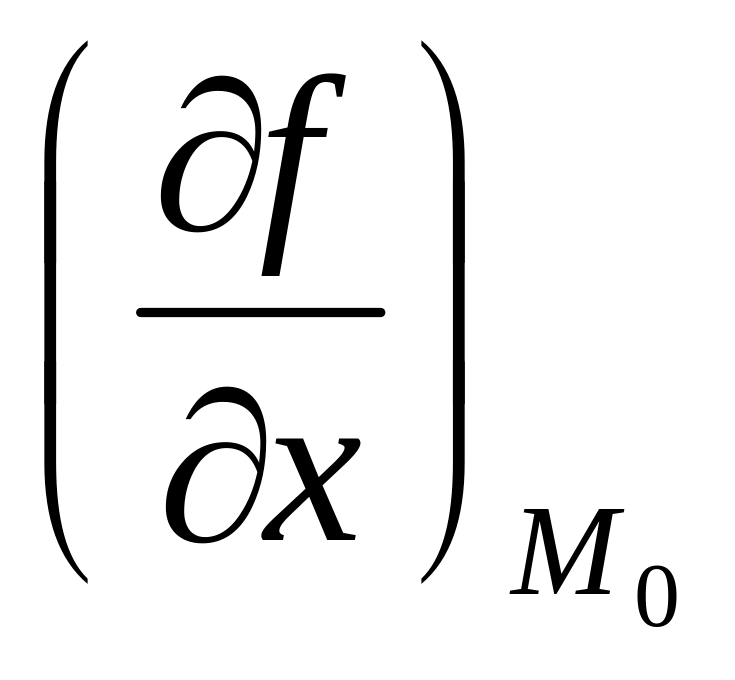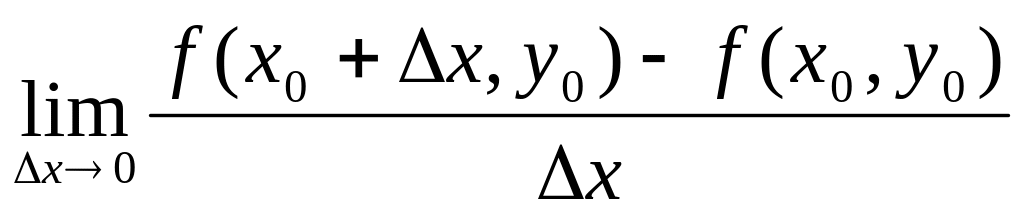1. = отв

1. 02 Для функции Z=f(x, y) частная производная по у в точке M₀(x_0, y₀) определяется формулой

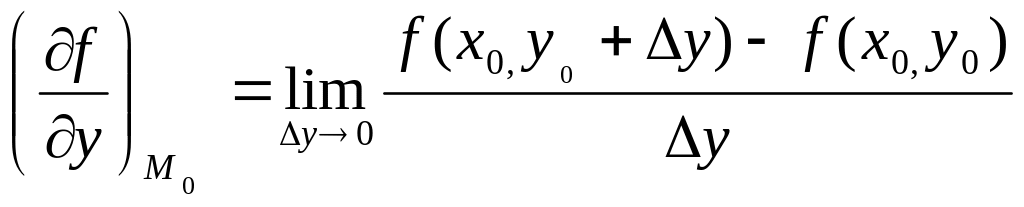1. отв

1. 03 Полное приращение функции Z=f(x, y) в точке M₀(x_0, y₀) представляется формулой:

1. ∆Z = f(x₀+∆x, y₀+∆y) - f(x_0,y₀) отв

1. 04 Полный дифференциал функции Z=f(x, y) равен

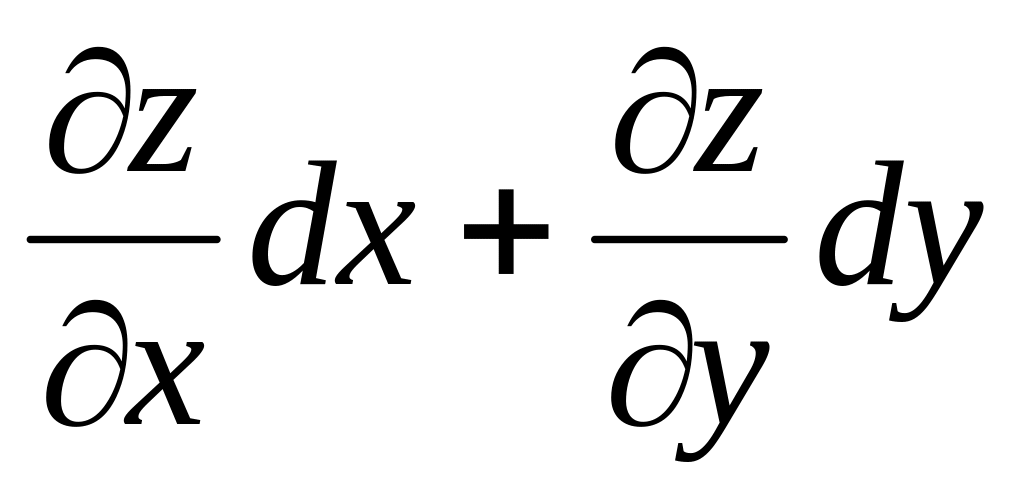1. dz= отв

1. 05 Если y=y(x) – непрерывная функция, заданная уравнением F(x, y)=0, где F(x, y), F^/_x(x, y), F^/_y(x, y) – непрерывные функции в области, содержащей точку M(x, y), в которой F^/_y(x, y)≠0, то производная функции y=y(x) в соответствующей точке существует и выражается формулой

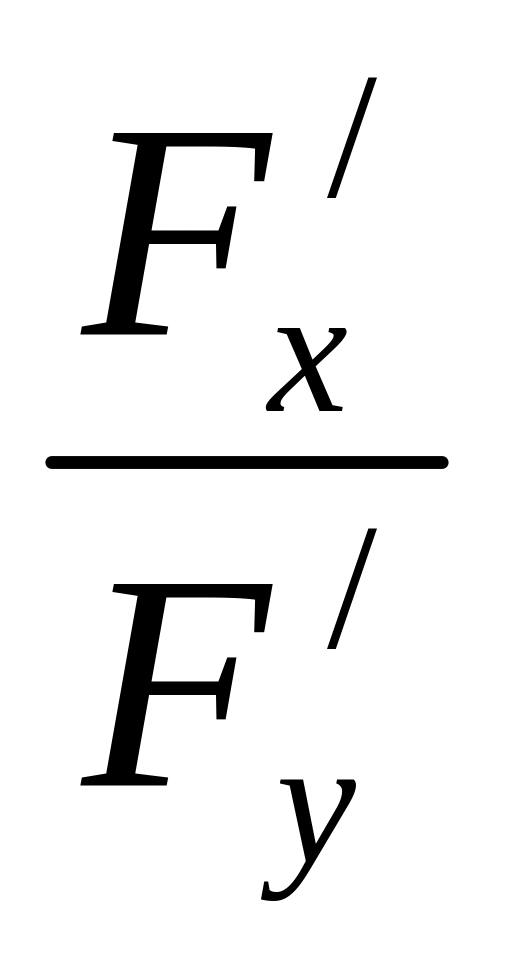1. y^/_x = - отв

1. 06 Если пространственная линия задана параметрическими уравнениями x=x(t), y=y(t), z=z(t), (α < t < β), то уравнение касательной к ней в точке M₀(x₀, y₀, z₀) имеет вид

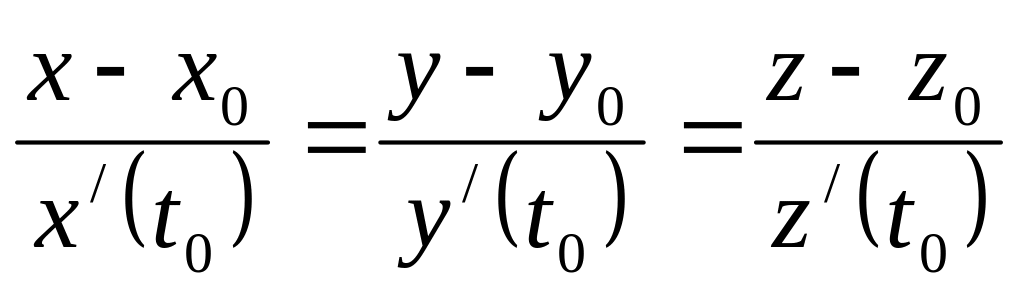1. отв

1. 07 Производная функции U=U(x, y, z) в точке М₀ (x₀, y₀, z₀) по направлению вектора выражается формулой

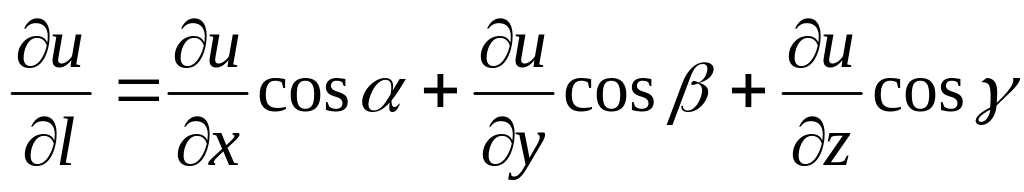1. отв

1. 08 Поле называется стационарным, если рассматриваемая величина не зависит от

1. времени отв

1. 09 Градиентом функции U= U(x, y, z) в точке называется

1. grad U = 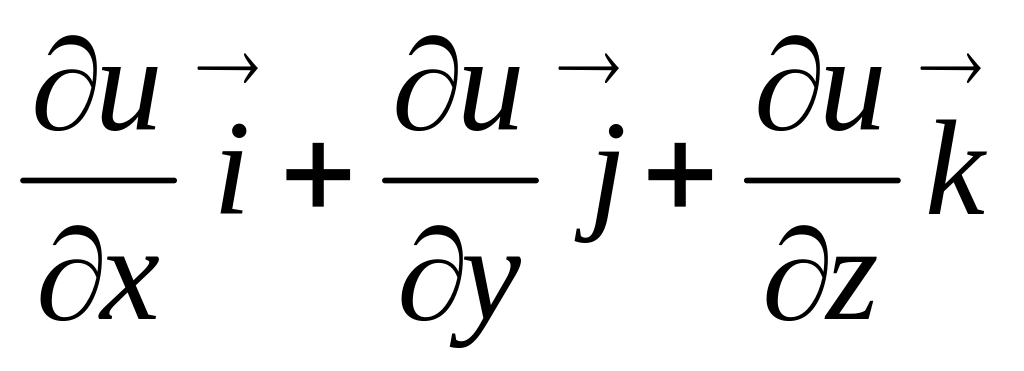отв

1. 10 Связь между градиентом функции и производный по направлению

1. 

2. 

3. 

4. 

5. 

1. 11 В точке экстремума дифференцируемой функции все ее первые частные производные

1. равны нулю отв

1. 12 Если функция z=f(x, y) имеет непрерывные первые и вторые частные производные в точке M₀ и в некоторой ее окрестности и первые частные производные в этой равны нулю, а вторые принемают значения , то точка является точкой минимума данной функций при

1. В²-АС>0 и А>0 отв

1. 13 Если функция z=f(x, y) имеет непрерывные первые и вторые частные производные в точке M₀ и в некоторой ее окрестности и первые частные производные в этой равны нулю, а вторые принемают значения , то точка M₀ является точкой максимума, данной функций при

1. В²-АС>0, А<0 отв

1. 14 Если функция z=f(x, y) имеет непрерывные первые и вторые частные производные в точке M₀ и в некоторой ее окрестности и первые частные производные в этой равны нулю, а вторые принемают значения , то в точке M₀ экстремума нет при

1. В²-АС>0

2. В²-АС≥0

3. В²-АС=0

4. В²-АС<0 отв

5. В²=-АС

1. 15 Если функция z=f(x, y) имеет непрерывные первые и вторые частные производные в точке M₀ и в некоторой ее окрестности и первые частные производные в этой равны нулю, а вторые принемают значения , то в точке M₀ вопрос о наличии экстремума остается открытым при

1. АС-В²=0 отв

1. 16 Что называется частным приращением функции f(x,y) по переменной х?

1. f(x₀+∆x, y₀) – f(x₀,y₀) отв

1. 17 Что называется частным приращением функции f(x,y) по переменной y?

1. f(x₀, y₀+∆y) – f(x₀,y₀) отв

1. 18 Производная функции в точке по направлению вектора имеет наибольшее значение, если направление совпадает

1. с направлением градиента данной функции отв

1. 19 Для поверхности z=f(x, y) уравнение касательной плоскости и в точке M₀ (x₀, y₀, z₀) принимает вид:

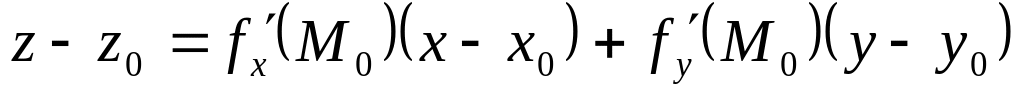1. отв

1. 20 Для поверхности z=f(x, y) уравнение нормали в точке M₀(x₀, y₀, z₀) принимает вид:

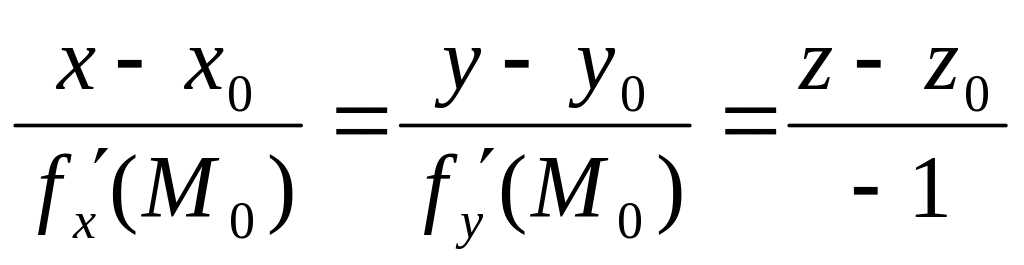2. отв

1. 21 Если смешанные частные произволные непрерывны, то результаты дифференцирования

1. не зависят от порядка дифференцирования отв

1. 22 Для функции z=f(x, y) дифференциал второго порядка определяется формулой

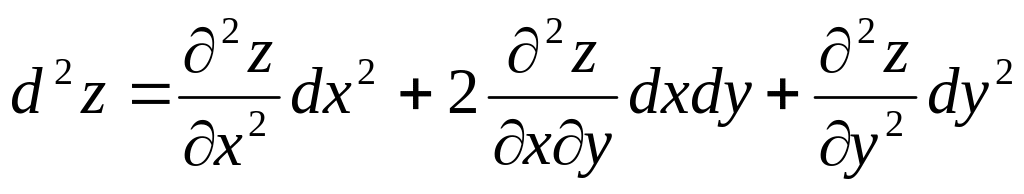1. отв

1. 23 Функция, имеющая полный дифференциал, называется

1. дифференцируемой отв

1. 24 x U=f(x, y, z)

1. ∆_xU=f(x+∆x, y, z)-f(x, y, z) отв

1. U=f(x, y, z)

1. ∆_yU=f(x,y+∆y, z)-f(x, y, z) отв