3. Контрольные вопросы.

1. Что характеризируют тангенциальное и нормальное ускорение?

2. Как связаны линейные и угловые характеристики движения?

3. Что называется плечом силы?

4. Что называется моментом силы?

5. Что такое момент инерции материальной точки?

6. Что представляет собой момент инерции тела?

7. От чего зависит момент инерции тела?

8. Какое тело называется абсолютно твердым?

9. Какое движение называется вращательным?

10. В чем заключается основной закон динамики вращательного движения?

4. Домашнее задание.

Для выполнения работы необходимо изучить следующие вопросы: линейная и угловая скорости. Тангенциальное, нормальное, полное и угловое ускорение. Момент силы. Момент инерции тела. Основной закон динамики вращательного движения.

5. Лабораторное задание.

Маятник Обербека (рис. 1) состоит из насаженных на одну ось двух шкивов разных диаметров d₁ и d₂ и крестовины, на которой закреплены гири (1, 2, 3, 4), на один из шкивов намотана нить, к концу которой прикреплен груз массой m.

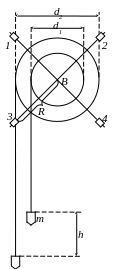
Рис. 1.

Если груз отпустить, то он приведет в ускоренное движение шкив и крестовину. При ускоренном движении груза m вниз сила натяжения нити будет:

, (22)

где - ускорение свободного падения ( ), а - линейное ускорение груза, численно равное тангенциальном ускорению точек поверхности шкива, из которого сматывается нить.

Сила, которая создает крутящий момент, численно равна и противоположно направленное силе натяжения и приложена к ободу шкива. Плечом этой силы есть половина диаметра d шкива, т.е. радиус шкива. Следовательно, крутящий момент

(23)

Если учесть пройденный ускоренно падающим грузом путь

, то

а угловое ускорение вращающихся частей, на основании формулы (15) будет

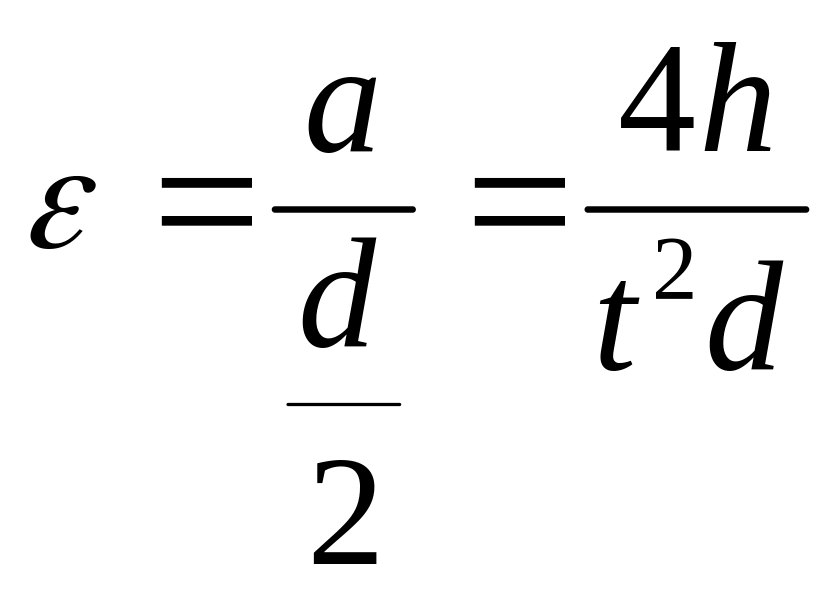(24)

Крутящий момент с учетом соотношения (24) будет иметь вид:

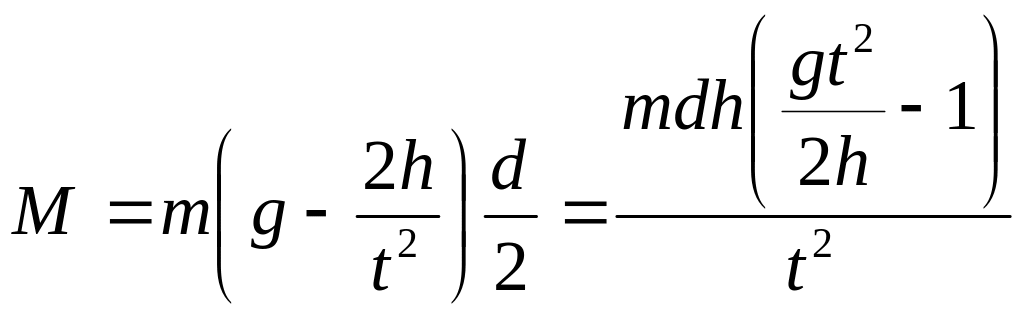(25)

В этом выражении величина , поэтому можно считать, что

(26)

Из основного закона динамики вращательного движения

(27)

А если подставить выражение (24), то получим:

. (28)

6. Порядок выполнения работы.

1. Закрепить грузики (1, 2, 3, 4) на крестовине на любых, но одинаковых расстояниях от оси вращения.

2. Измерить штангенциркулем диаметры шкивов d₁ и d₂.

3. Намотать нить с грузом m на шкив диаметром d₁ и, дав грузу возможность свободно падать, привести маятник во вращение.

4. Определить с помощью линейки путь h, пройденный грузом и время t прохождения этого пути с помощью секундомера.

5. Опыт проделать 3 раза для одинакового пути h, и найти среднее арифметическое значение времени .

6. Такие же измерения провести, наматывая нить на шкив диаметром d₂.

7. Используя формулы (24) и (26) вычислить отношение угловых ускорений и вращательных моментов.

8. Результаты измерений и вычислений записать в таблицу 1.

Таблица 1.

d1(мм)	d2(мм)	ε1( )	ε2( )

9. Сравнивая величины ε₁/ε₂ и M₁/M₂, сделать выводы о справедливости основного закона динамики вращательного движения.

10. Изменяя положение грузиков 1, 2, 3, 4 на крестовине (их надо располагать симметрично относительно оси вращения), проработать 5 опытов для одного из диаметров шкива (d₁ или d₂).

11. В каждом опыте при том же h время измерять 3 раза и найти среднее арифметическое значение времени. В каждом опыте измерить расстояние R от грузиков (1, 2, 3, 4) до оси вращения B.

12. По формуле (28) 5 раз вычислить момент инерции.

13. Результаты измерений и вычислений поместить в таблицу 2.

Примечание: масса падающего груза указана непосредственно на нем и определена с погрешностью ∆m = ± 1г

Таблица 2

№ п/п	R (м)	m (кг)	d (м)	h (м)	t, с	I (кг м2)
1
2
3
4
5

14. Построить график зависимости I = f (R²) и сделать вывод о характере этой зависимости.

7. Приборы и оборудование.

Маятник Обербека, длинная линейка, секундомер, штангенциркуль.

8. Литература.

1. Савельєв И. В. Курс общей физики, т.1 изд. “Наука” , 1987г 3.7-11, 34-38.

2. Зисман Г. А., Тодес О. М. Курс общей физики т.1 изд. “Наука” , 1969р. 2, 10, 11.

Лабораторное занятие №4