6. Порядок выполнения работы:

1. Проверить, чтобы до удара шарики касались и чтобы их центры масс были на одном уровне.

2. Определить длину подвеса шаров.

3. Отклонить один из шариков на угол , измерить величину этого угла и отпустить шар для удара.

4. Измерить угол отклонения второго шара после удара .

5. Опыт проделать 3 раза при одном и том же и найти среднее арифметическое значение .

6. Результаты измерений занести в таблицу 1

Таблица 1.

№

, кг

, кг

, м

, м

, град

, град

, град

, град

, град

, град

, кгм/с

, кгм/с

, Дж

, Дж

1 2 3

7. Вычислить:

- Средние квадратические погрешности прямых измерений по методу Стьюдента;

- Относительные погрешности косвенных измерений импульса до удара и после удара по формуле:

,

- по формуле (16) импульсы шаров до удара и после удара ;

- абсолютные погрешности импульсов до удара и после удара по формуле: ;

- относительные погрешности косвенных измерений кинетической энергии до удара и после удара по формуле:

,

- по формуле (17) кинетические энергии шаров до удара , и после удара ;

- абсолютные погрешности кинетических энергий шаров до удара и после удара по формуле: ;

8. Результаты вычислений записать в виде:

… при =…% … при =…%

… при =…% … при =…%

9. В заключении к работе сравнить величины и , и .

6. Приборы и оборудование.

Двa упругиx шарикa известной массы на бифилярном подвесе, рулетка, штангенциркуль, угломерная шкала с ценой деления 1°.

7. Литература.

1.Савельев И.В., Курс общей физики, т.1, “Наука”, 1986, § 27,28.

2.Зисман г.А., Тодес о.М., Курс общей физики, т.1, “Наука”, 1969, § 4,6,8.

Лабораторное занятие № 3

Вариант 1 Исследование зависимости момента инерции тела от положение оси вращения

1. Цель работы.

Определить момент инерции тела при трех различных положениях оси вращения.

2. Теоретические сведения.

Вектор линейной скорости направлен по касательной к траектории движения и по величине равен первой производной от пути по времени:

(1)

Вектор ускорения равен границе отношения прироста вектора скорости к промежутку времени , за которое он произошел, при условии, что этот промежуток времени стремится к нулю, то есть ускорение равно первой производной от вектора скорости по времени:

(2)

В любом случае вектор можно разложить на тангенциальную та нормальную составляющие:

(3)

Поэтому вектор можно представить суммой двух величин:

(4)

В выражении (4) величину:

(5)

называють тангенциальным ускорением, а величину:

(6)

нормальным ускорением.

Ускорение , которое называется полным, является векторной суммой и , то есть:

(7)

Можно доказать, что по величине:

(8)

, (9)

где R- радиус кривизны траектории движения в рассматриваемый момент времени.

Тангенциальное ускорение направлено по касательной к траектории движения и характеризует изменение вектора скорости по числовому значению. Если движение ускоренное, то совпадает по направлению с (рис. 1а), а если замедленное то направлено противоположно (рис. 1б). Если скорость по величине не изменяется, то .

Нормальное ускорение направлено по радиусу к центру кривизны траектории движения (оно называется также центростремительным) и характеризует изменение скорости по направлению.

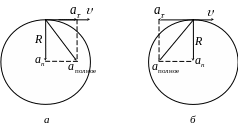
Рис. 1.

Поскольку та всегда взаимно перпендикулярны, то по величине:

(10)

При вращательном движении материальной точки, линейная скорость:

, (11)

где l – длина дуги траектории.

Поскольку , то

, (12)

где — угловая скорость материальной точки. Она численно равна углу поворота в единицу времени. Единицы измерения в СИ – [ω] = [ ].

В общем случае угловая скорость имеет смысл вектора, направленного по оси вращения (осевого вектора). Этот вектор направлен так, чтобы, глядя ему вслед, можно было бы видеть вращения материальной точки по часовой стрелке, тогда (рис. 2).

Угловым ускорением называют величину, численно равную первой производной от угловой скорости по времени:

(13)

Единицы измерения в СИ – [] = [ ]. В векторной форме, соответственно:

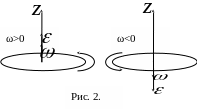
Угловое ускорение тоже имеет смысл осевого вектора, направление которого совпадает с направлением вектора угловой скорости при ускоренном движении и противоположный ему - при замедленном движении (рис. 2).

Между линейными и угловыми характеристиками движения существует следующая взаимосвязь:

(14)

(15)

(16)

(17)

Абсолютно твердое тело (АТТ) - это тело, которое не деформируется ни при каких воздействиях. В абсолютно твердом теле относительное положение его частиц в процессе движения не меняется.

Вращательным называется движение тела, при котором все точки описывают круги, центры которых лежат на оси вращения.

Моментом силы М относительно некоторой оси вращения z (вращательным моментом) называется величина, численно равная произведению действующей на тело силы F на плечо h, то есть:

M_z=Fh (18)

В общем случае момент силы это величина векторная: .

Плечом силы называется кратчайшее расстояние от оси вращения до линии действия (направления) этой силы.

Инертность вращающегося тела зависит от распределения его массы относительно оси вращения и характеризуется величиной, которая носит название момента инерции I. Различают момент инерции материальной точки и момент инерции АТТ.

Моментом инерции материальной точки относительно оси z называется величина, численно равная произведению массы точки m на квадрат расстояния от нее до центра вращения r:

(19)

Момент инерции АТТ относительно оси z является суммой моментов инерции всех точек, из которых это тело состоит:

(20)

Момент инерции АТТ зависит как от его формы, массы и размеров, так и от расположения оси вращения. Для тела в форме параллелепипеда:

, (21)

де m - масса тела, і - размеры тела, показаны на рис. 3

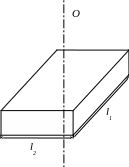
Рис. 3.

Основной закон вращательного движения для АТТ заключается в том, что крутящий момент М_z и угловое ускорение ε, полученное телом под действием этого момента, прямо пропорциональны и записываются в виде:

(22)