3. Описание установки.

Для изучения затухающих колебаний нужно собрать схему с генератором затухающих колебаний, удобно рассматривать на экране осциллографа. Такая схема представлена на рис. 3.

Рис. 3.

а колебательный контур, состоящий из конденсатора С, индуктивности L, и сопротивления R, от генератора через конденсатор направляются периодические П-образные импульсы напряжения. Каждый импульс возбуждает в колебательном контуре затухающие колебания. Эти колебания накладываются друг на друга и на экране осциллографа можно получить устойчивую картинку затухающих колебаний.

Включая в колебательный контур различные активные сопротивления, можно изучить их влияние на характер затухания колебаний.

4. Приборы и оборудование.

1. Установка для изучения затухающих колебаний.

2. Генератор П-образных импульсов.

3. Осциллограф.

4. Соединительные проводники

5. Порядок выполнения работы.

1. Собрать схему согласно рис. 2.

2. Включить осциллограф.

3. Добиться четкого изображения развернутого луча на экране.

4. Включить генератор П-образных импульсов. Подать напряжение на осциллограф и добиться устойчивого изображения колебаний на экране осциллографа.

5. Замерить (в относительных единицах) два соседних значения амплитуды для трех значений активного сопротивления .

6. Рассчитать логарифмический декремент и добротность колебательной системы для этих значений R.

7. Данные измерений и расчетов занести в таблицу:

№	R, Ом	Аn	An-1	δ	Q	ΔQ
1 2 3

8. В выводах дать оценку полученному результату

Задание 2.

1. Цель работы.

Изучить вынужденные колебания в колебательном контуре. Определить зависимость амплитуды тока в колебательном контуре от частоты и зависимость резонансной частоты от активного сопротивления R, индуктивности L и емкости С.

2. Теоретические сведения.

В технике очень часто нужны незатухающие колебания. Например, в колебательных контурах радиопередатчиков. Незатухающие - это вынужденные колебания, колебания, возникающие под действием дополнительной переменной внешней силы, которая пополняет уменьшению энергии в колебательном контуре.

Пусть в колебательном контуре действует переменная ЭДС .

Рис. 4

По второму закону Кирхгофа:

Отсюда имеем:

или

, (15)

где

(16)

. (17)

Решением дифференциального уравнения (15) является гармоничная функция:

. (18)

Амплитуда и начальная фаза Ψ определяются из соотношений:

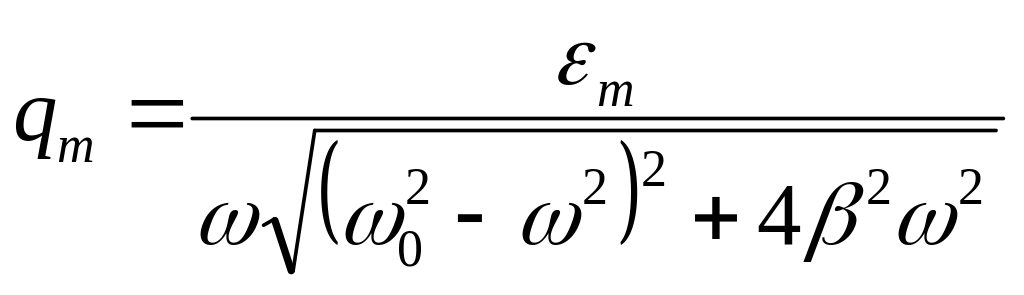(19)

(20)

Напряжение на конденсаторе изменяется так же, как и заряд:

(21)

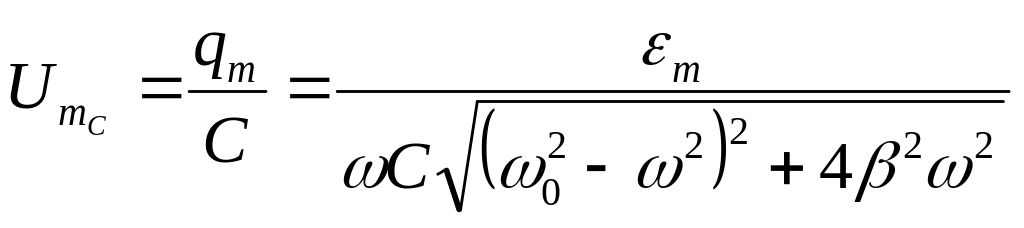. (22)

Амплитуда напряжения (и заряда) зависит от частоты.

Найдем выражение для силы тока. Используя (18), имеем:

,

где

. (23)

Подставим в (23) выражение для (19):

. (24)

Учитывая, что та уравнения (24) можем записать в виде:

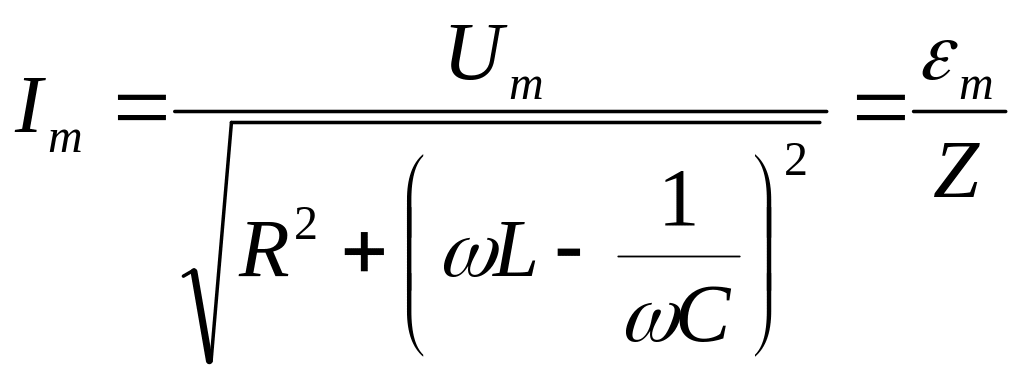. (25)

Тут - полное электрическое сопротивление, состоящее из активного сопротивления R, индуктивного и емкостного .

При имеем максимум амплитуды тока - резонанс тока. Отсюда , то есть резонанс тока реализуется при резонансной частоте, равной частоте собственных колебаний контура. Увеличение емкости С или индуктивности L уменьшает резонансную частоту, что качественно изображено на рис. 5, а и б.

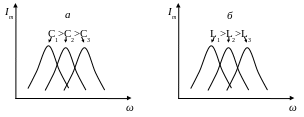
Рис. 5.

При резонансе амплитуда тока становится максимальной и зависит от активного сопротивления:

На графике зависимость амплитуды тока от частоты изображается следующим образом:

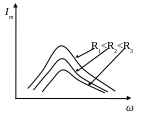
Рис. 6.

При ток в колебательном контуре отсутствует (через конденсатор постоянный ток не протекает).