Дифференциальная форма уравнений (1) и (2)

( - плотность тока).

Применение закона полного тока для расчета .

1. Поле бесконечного соленоида.

Ч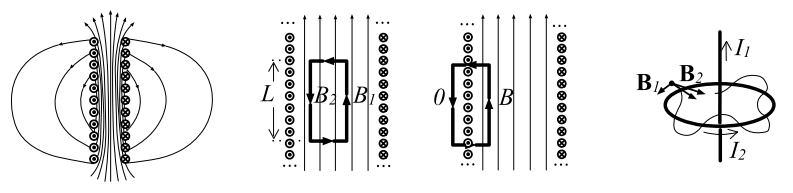 исло витков на единицу длины соленоида равно , сила тока I.

Токи в витках обозначены точками (на нас) и крестиками (от нас).

Из симметрии очевидно, что линии направлены вдоль оси соленоида параллельно друг другу.

Покажем, что поле внутри соленоида однородно, т.е. его индукция одинакова во всех точках. Запишем циркуляцию для прямоугольного контура, лежащего внутри соленоида (рис. слева): , или .

Возьмем теперь контур (рис. справа), одна сторона которого лежит внутри соленоида, другая – снаружи. Снаружи бесконечного соленоида . Контур охватывает nL витков с током, поэтому , или

.

Эту формулу можно применять к достаточно длинным соленоидам, у которых длина гораздо больше диаметра.

2. Магнитное поле тороида.

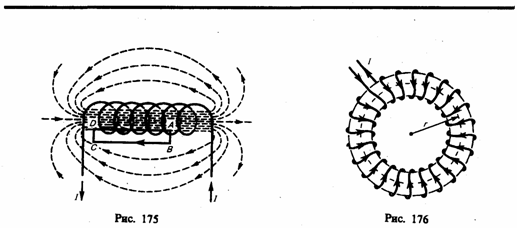
Тороид представляет собой тонкий провод, плотно (виток к витку) намотанный на каркас в форме тора.

Пусть N – полное число витков.

Вне тора . Линии В внутри тора, очевидно, представляют собой концентрические окружности. Циркуляция по контуру радиуса r

,

т.к. контур охватывает все N витков. Поэтому

.

Закон полного тока позволяет решить очень ограниченное число задач - таких, симметрия которых позволяет выделить простые для расчета циркуляции контуры.

Закон же Био-Савара-Лапласа – это универсальный метод расчета магнитного поля.

§ 7. Работа силы Ампера

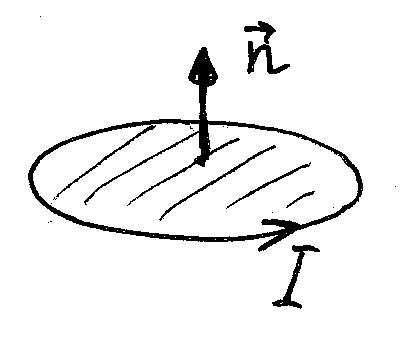
Рассмотрим замкнутый контур с током I, находящийся во внешнем магнитном поле, которое создает магнитный поток Ф сквозь контур. (Напомним, что поток сквозь контур – это поток через поверхность, натянутую на контур.) При расчете потока будем считать, что направление положительной нормали к поверхности связано с направлением тока в контуре правилом правого винта.

Покажем, что при любых перемещениях контура с током I работа силы Ампера, действующей на него, зависит от изменения магнитного потока:

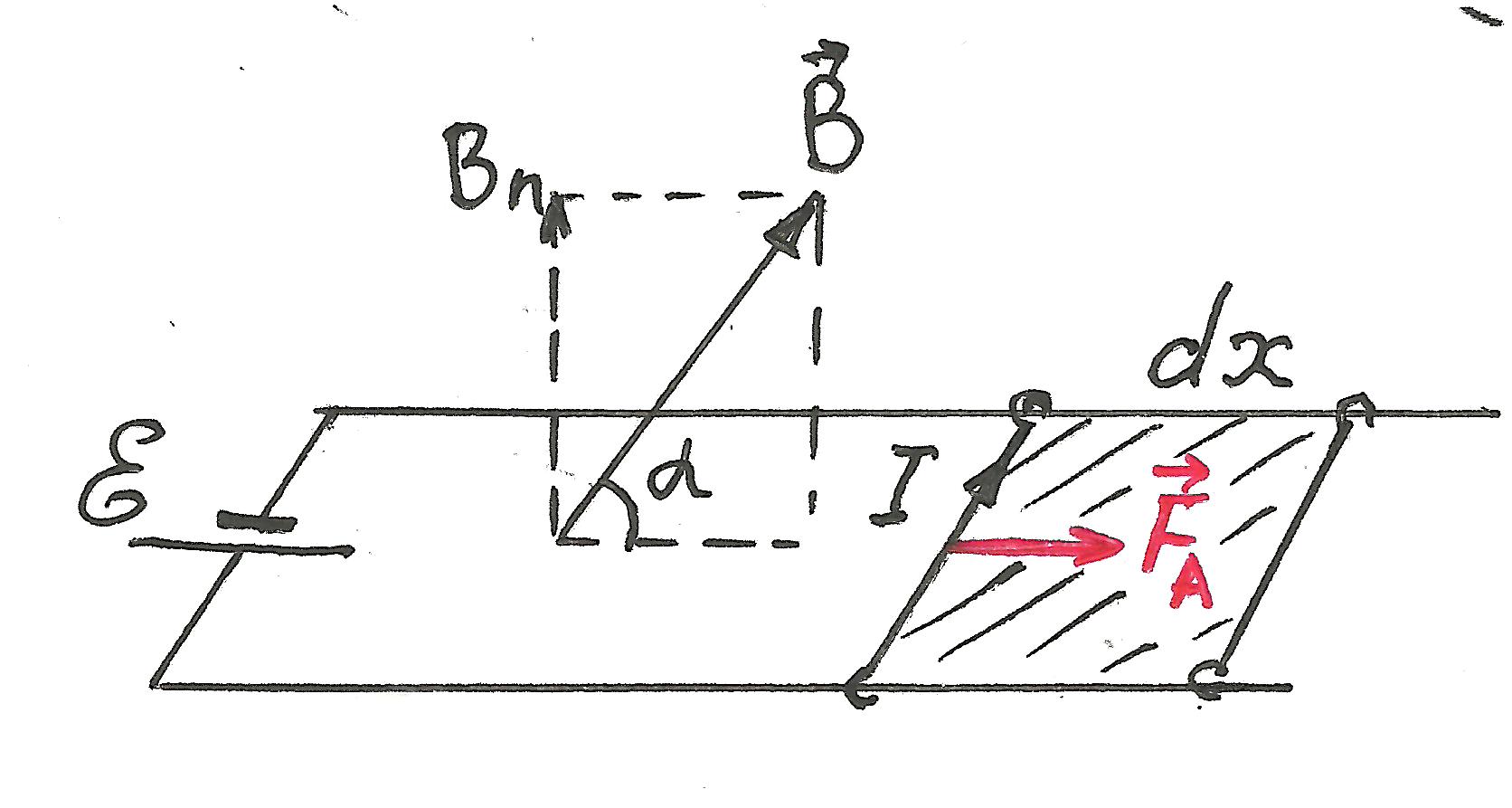
1) Рассмотрим сначала частный случай: прямоугольный контур с подвижной перемычкой длины l. Однородное магнитное поле направлено под углом к плоскости контура. На перемычку с током I действует сила Ампера , где - нормальная составляющей поля. Если перемычка переместилась на расстояние x, «заметая» при этом площадь , то сила Ампера совершила работу .

Работа силы Ампера определяется изменением потока сквозь контур, которое в свою очередь определяется «заметаемой» при движении проводника площадью.

2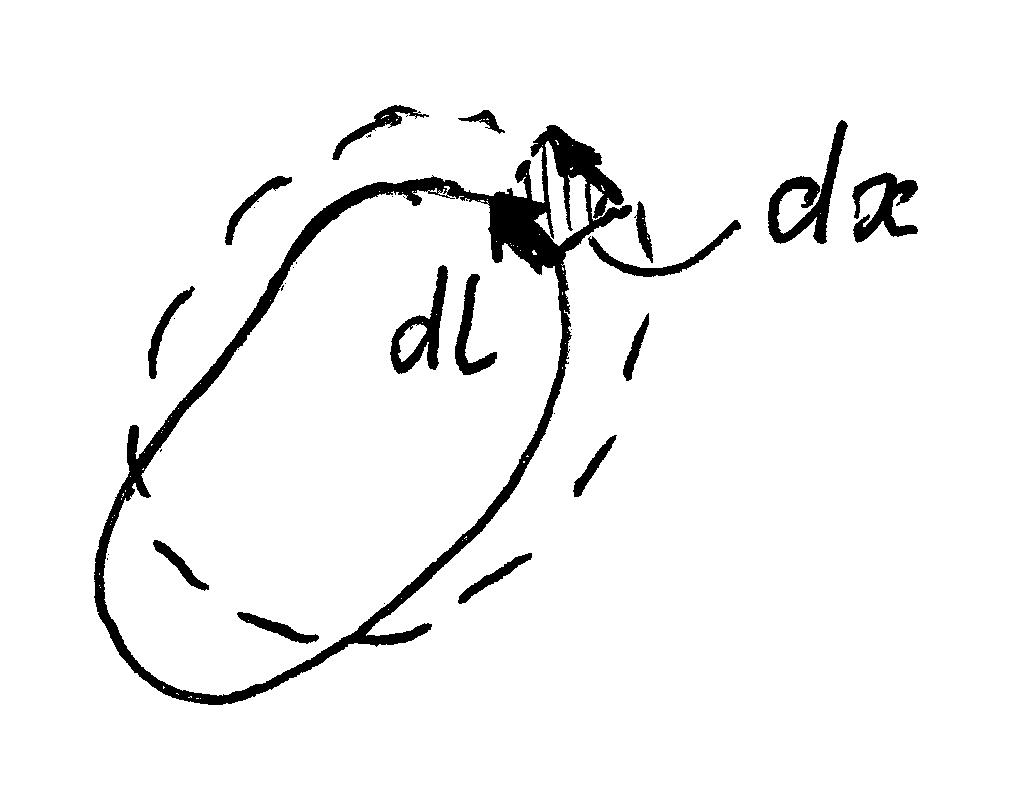 ) Рассмотрим теперь контур произвольной формы. Разобъем контур на малые элементы тока Idl. При произвольном перемещении контура каждый элемент тока перемещается на некоторое расстояние dx, заметая при этом площадь . Работа силы Ампера, действующей на элемент тока, определяется заметаемой им площадью dS и связанным с этой площадью изменением потока: . Полную работу силы Ампера находим суммированием по всем элементам тока:

.

Если при перемещении контура сила тока в нём поддерживается постоянной, то

,

где Ф₂ и Ф₁ – соответственно конечный и начальный магнитные потоки.

Эта формула дает не только величину, но и правильный знак совершаемой работы, если при расчете потоков выбирать положительную нормаль, связанную с током правовинтовым соотношением.