§ 4. Закон Био-Савара-Лапласа
П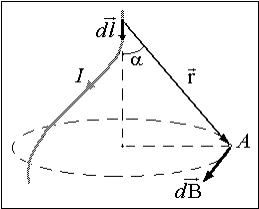
озволяет
вычислить магнитное поле провода с
током произвольной формы.
Разобьем провод на бесконечно малые
элементы тока
.
Поле провода есть суперпозиция полей
всех элементов тока. Модель элемента
тока аналогична модели точечного заряда
в электростатике.
Закон Био-Савара-Лапласа определяет
поле
элемента тока в произвольной точке А.
Это экспериментальный закон (Био и Савар
измеряли поле проводов с током, Лаплас
ввел понятие элемента тока и нашел
правильную форму закона).
Пусть
- радиус-вектор, проведенный от элемента
тока к точке А,
- угол, который он образует с осью элемента
тока. Магнитная индукция в точке А
.
Размерный коэффициент пропорциональности
в этой формуле принято обозначать
(
называют магнитной постоянной;
Тл·м/А
). Итак:
.
(1)
перпендикулярна векторам
и
,
т.е. перпендикулярна плоскости рисунка
(в которой лежат оба эти вектора).
В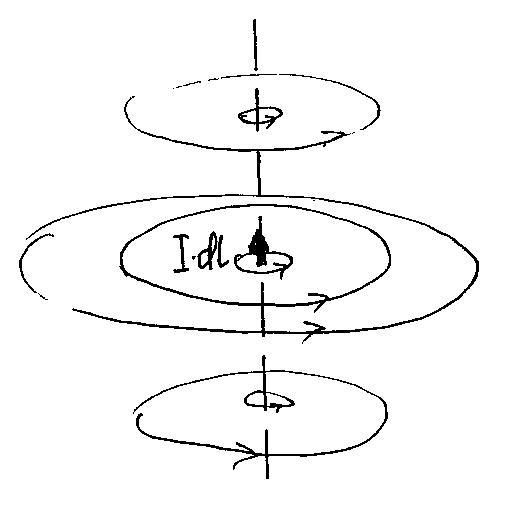
скалярном виде:
. (2)
Если бы мог существовать отдельный
элемент тока, то его магнитное поле
выглядело бы так: линии индукции - это
набор окружностей, центры которых лежат
на оси тока. Модуль магнитной индукции
убывает обратно пропорционально квадрату
расстояния от элемента тока – в этом
поле элемента тока похоже на
электростатическое поле точечного
заряда. При одинаковых значениях
расстояния r магнитная
индукция dB максимальна
в плоскости, проходящей через элемент
тока перпендикулярно его оси (
).
На оси тока
.
С помощью закона Био-Савара-Лапласа и принципа суперпозиции можно рассчитать поле любой формы провода с током.
Примеры расчета полей с помощью закона Био-Савара-Лапласа
Поле кругового тока. Радиус витка R, сила тока I – см. решение задачи 7.6.
В центре витка
,
на оси витка
.
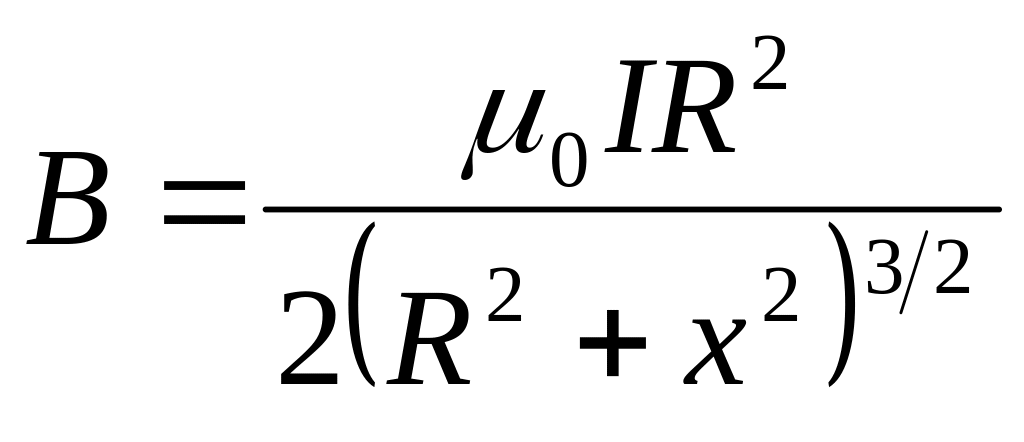Определение: произведение силы тока
в витке на его площадь называют
магнитным моментом витка:
.
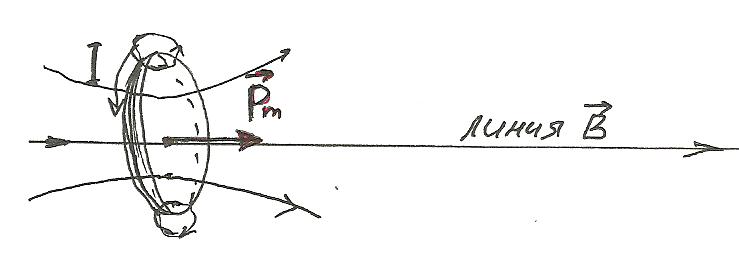
Магнитный момент – вектор, направленный
перпендикулярно плоскости витка и
связанный с направлением тока в витке
правилом правого винта.
2. Магнитное поле прямого провода.
Поскольку поле есть суперпозиция полей всех элементов тока, а линии индукции каждого элемента тока представляют собой окружности с центрами на оси тока, то суммарное поле выглядит так же.
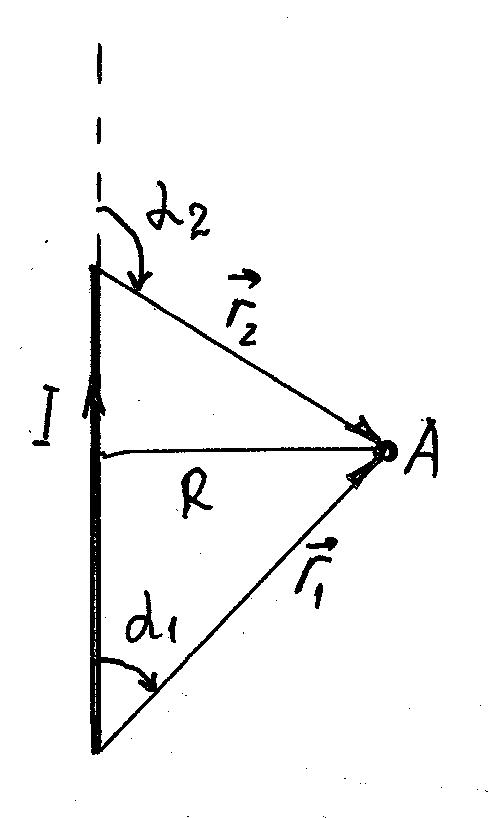
Пусть А – точка, в которой мы вычисляем индукцию В. Кратчайшее расстояние от этой точки до провода R. Рассмотрим элемент тока Idl. Радиус-вектор , проведенный от него к точке А, образует угол с осью тока. Поле этого элемента в точке А
. (2)
Выразим все величины через одинаковое
для всех элементов тока расстояние R
и угол
,
по которому затем будет производиться
интегрирование:
;
элемент тока виден из точки А под углом
,
причем
,
или
.
Подставив выражения для r
и dl в формулу (2),
получим:
.
Интегрирование по всем элементам тока
сводится к интегрированию по углу
в пределах от
до
- углов, образуемых радиусами-векторами,
проведенными от концов провода к точке
А, с осью тока:
. (3)
При применении формулы (3) обратите внимание на правильный отсчет углов и , как это показано на рисунке: углы отсчитываются от оси тока к радиусам-векторам.