
- •§ 1. Свойства проводников в электростатическом поле
- •Поле вблизи поверхности проводника.
- •Эквипотенциальность проводника.
- •Распределение заряда на проводнике.
- •5) Вычисление е вблизи поверхности проводника.
- •6) Электрические силы, разрывающие проводник.
- •7) Свойства замкнутой проводящей оболочки.
- •Заряд в полости проводника.
- •§ 2. Метод зеркальных изображений
- •§ 3. Электроемкость проводников и конденсаторов
- •Электроемкость конденсатора
- •Соединение конденсаторов в батереи
- •§ 4. Электрическая энергия заряженного проводника и конденсатора
- •Энергия заряженного проводника
- •Энергия заряженного конденсатора
- •Плотность энергии
§ 3. Электроемкость проводников и конденсаторов
Электроемкость уединеннного проводника (удалённого от других зарядов и проводников)
Электроемкость уединенного проводника — это скалярная физическая величина, равная отношению электрического заряда проводника к его потенциалу:
В СИ единицей электроемкости является фарад (Ф): 1 Ф — это электроемкость такого проводника, потенциал которого становится равным 1 В при сообщении ему заряда в 1 Кл.
Поскольку 1 Ф очень большая единица емкости, чаще применяют единицы: 1 пФ (пикофарад) = 10-12 Ф, 1 нФ (нанофарад) = 10-9 Ф, 1 мкФ (микрофарад) = 10-6 Ф и т.д.
Э
 лектроемкость
проводника зависит от его формы и
размеров. Она не
зависит от заряда проводника. (проводник
может быть не заряжен – всё равно он
обладает электроемкостью.)
лектроемкость
проводника зависит от его формы и
размеров. Она не
зависит от заряда проводника. (проводник
может быть не заряжен – всё равно он
обладает электроемкостью.)
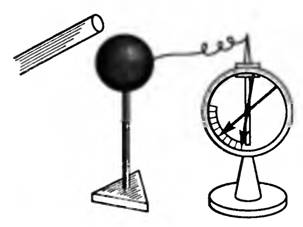
С зависит также от наличия вблизи других проводников или диэлектриков. Действительно, приблизим к заряженному шару, соединенному с электрометром, незаряженную палочку (рис. 1). Он покажет уменьшение потенциала шара (из-за индуцированных на палочке зарядов противоположного знака). Заряд q шара не изменился, следовательно, увеличилась его емкость.
Электроемкость изолированного шара радиуса R.
При сообщении шару заряда
q
его потенциал становится равным
![]() .
Емкость
.
Емкость
![]() .
.
Для примера, емкость Земного шара С=0,7 мФ.
С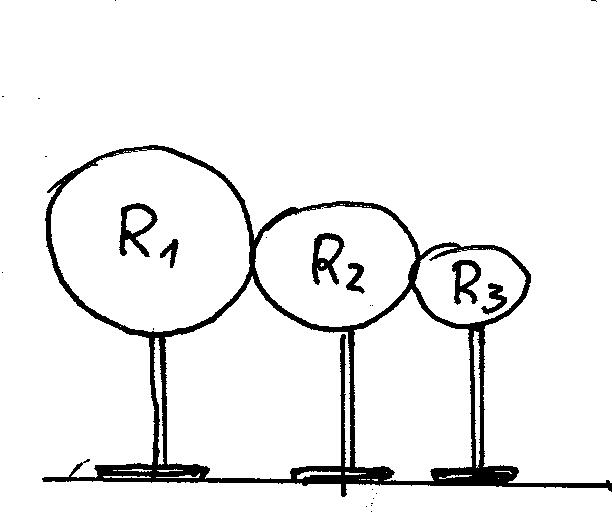 =1 Ф для шара радиуса 9 млн. км (в 15000 раз
больше радиуса Земли).
=1 Ф для шара радиуса 9 млн. км (в 15000 раз
больше радиуса Земли).
Демонстрация: зависимость емкости шаров от радиуса. Разделяем шары и сравниваем их заряды.
Электроемкость конденсатора
Д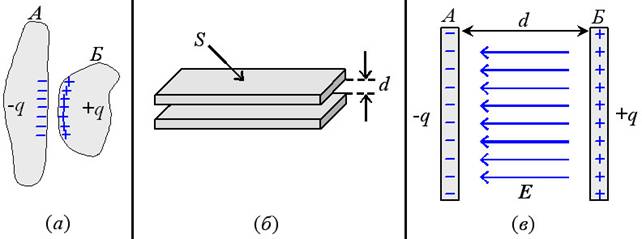 ва
проводника, заряженных равными по
величине разноименными зарядами образуют
конденсатор. Между проводниками (их
называют обкладками) может быть вакуум
или диэлектрическая среда.
ва
проводника, заряженных равными по
величине разноименными зарядами образуют
конденсатор. Между проводниками (их
называют обкладками) может быть вакуум
или диэлектрическая среда.
Разность потенциалов между обкладками называют также напряжением (U).
Модуль заряда q каждой из обкладок называют зарядом конденсатора.
Электроемкость С конденсатора — это скалярная физическая величина, равная отношению заряда q конденсатора к напряжению U:
С зависит от формы, размеров обкладок и свойств среды вокруг них.
С не зависит от заряда конденсатора.
А ) Емкость плоского конденсатора.
Пусть расстояние между пластинами d, площадь пластин S. Для начала будем считать, что между пластинами – вакуум.
Электрическое поле в основном сосредоточено в пространстве между обкладками, но некоторые линии напряженности всё же выходят наружу (рис. 1):

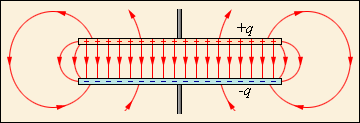
Рис. 1 Рис. 2
Мы будем пренебрегать краевыми эффектами и считать, что поле между обкладками однородно, а заряд распределен равномерно (рис. 2).
Если заряд конденсатора q,
то его поверхностная плотность
![]() ,
напряженность между пластинами
,
напряженность между пластинами
![]() .
В однородном поле разность потенциалов
между пластинами
.
В однородном поле разность потенциалов
между пластинами
![]() .
Емкость
.
Емкость
Для увеличения емкости надо увеличивать площадь пластин и уменьшать расстояние между ними.
Д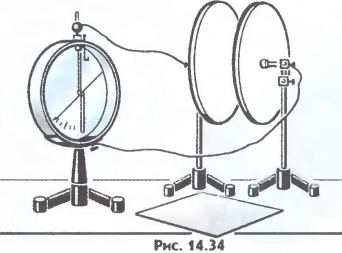 емонстрация:
зависимость емкости
плоского конденсатора от S
и d.
емонстрация:
зависимость емкости
плоского конденсатора от S
и d.
Заряд пластин q неизменен.
А) Увеличиваем d – и Е не меняются, U увеличивается, значит, С уменьшается.
Б) Уменьшаем S – возрастают и Е, U увеличивается, значит, С уменьшается.
В) При внесении стеклянной пластины между обкладками U уменьшается, значит, С увеличивается.
Вывод: диэлектрическая прослойка между обкладками увеличивает емкость конденсатора. Если диэлектрик заполняет всё пространство между обкладками плоского конденсатора, то
![]() .
.
Безразмерное положительное
число
![]() называют диэлектрической
проницаемостью.
называют диэлектрической
проницаемостью.
Для стекла
![]() ,
для парафина
,
для парафина
![]() .
.
Б) Емкость сферического конденсатора
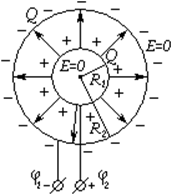
Сферический конденсатор хорош тем, что
поле целиком сосредоточено между
обкладками. Его напряженность
![]() .
.
Разность потенциалов между ними
 .
.
Емкость
 .
.
Если расстояние между обкладками мало:
![]() <<
<<![]() ,
то
,
то
![]() - как у плоского конденсатора (где
- как у плоского конденсатора (где
![]() - площадь обкладок).
- площадь обкладок).
Если всё пространство между обкладками заполнить диэлектриком, емкость увеличится в раз.
В) Емкость длинного цилиндрического конденсатора
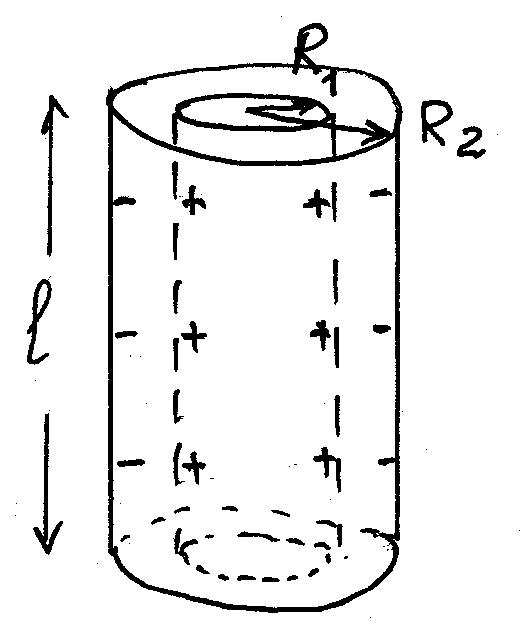
Чтобы можно было пренебречь краевыми
эффектами (как в плоском конденсаторе),
длина его
![]() должна быть много больше радиусов
обкладок. Тогда можно считать, что
снаружи
.
должна быть много больше радиусов
обкладок. Тогда можно считать, что
снаружи
.
Линейная плотность заряда обкладок
![]() .
Напряженность поля между обкладками
.
Напряженность поля между обкладками
![]() .
.
Напряжение между ними
 .
.
Емкость
 .
.
