7) Свойства замкнутой проводящей оболочки.

Если удалить внутреннюю (незаряженную) часть проводника, распределение заряда по его внешней поверхности и электрическое поле снаружи не изменятся.

Другими словами, поле и распределение зарядов по внешней поверхности полого проводника такие же, как и для сплошного проводника той же формы.

На внутренней поверхности полости зарядов нет.

Электрическое поле не проникает в полость проводника.

Н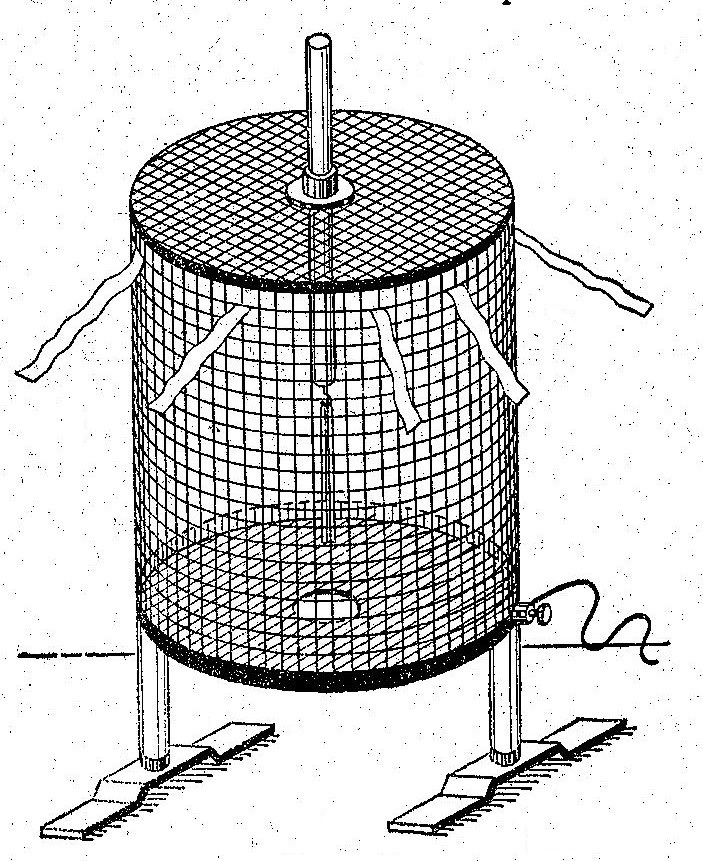 а этом основана электростатическая защита – экранирование приборов от влияния внешних полей.

Демонстрация:

«клетка Фарадея».

Листочки фольги снаружи становятся перпендикулярно сетке (вдоль линий напряженности), листочки внутри клетки не расходятся.

Фарадей в 1836 г. сам забрался внутрь большой клетки с электроизмерительными приборами.

Фото: человек в клетке Фарадея.

Заряд в полости проводника.

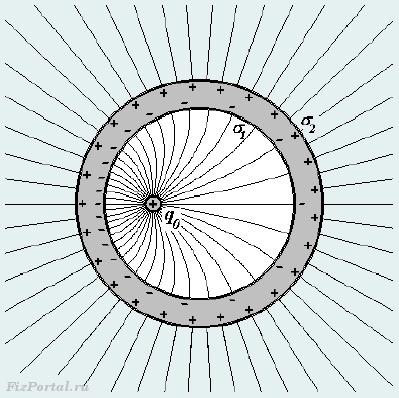Поле, создаваемое зарядом , не может проникнуть в толщу проводника. На внутренней поверхности полости возникает индуцированный заряд . Найдём его с помощью теоремы Остроградского-Гаусса: возьмём замкнутую поверхность, целиком лежащую в толще проводника. Поток через неё равен нулю, так как . С другой стороны, . Значит, .

При перемещении заряда внутри полости распределение заряда на внутренней поверхности полости изменяется так, чтобы поле не проникало в толщу проводника.

Если проводник в целом нейтрален, на его внешней поверхности индуцируется заряд . Этот заряд распределится так же, как если бы проводник был сплошным. Например, если проводник сферический, на внешней поверхности заряд распределится равномерно; внешний наблюдатель увидит снаружи центрально-симметричное поле. Перемещения заряда внутри полости никак не отражаются на поле снаружи.

Замкнутая проводящая оболочка разделяет всё пространство на внутреннюю и внешнюю области, в электрическом отношении не зависящие друг от друга.

§ 2. Метод зеркальных изображений

Пусть известна форма и потенциалы двух проводников. Как найти поле в любой точке пространства, силу взаимодействия проводников, распределение заряда на них?

В теории поля доказывается, что задача о нахождении поля между проводниками имеет единственное решение (с физической точки зрения это очевидно: поле однозначно определяется формой и потенциалами проводников).

И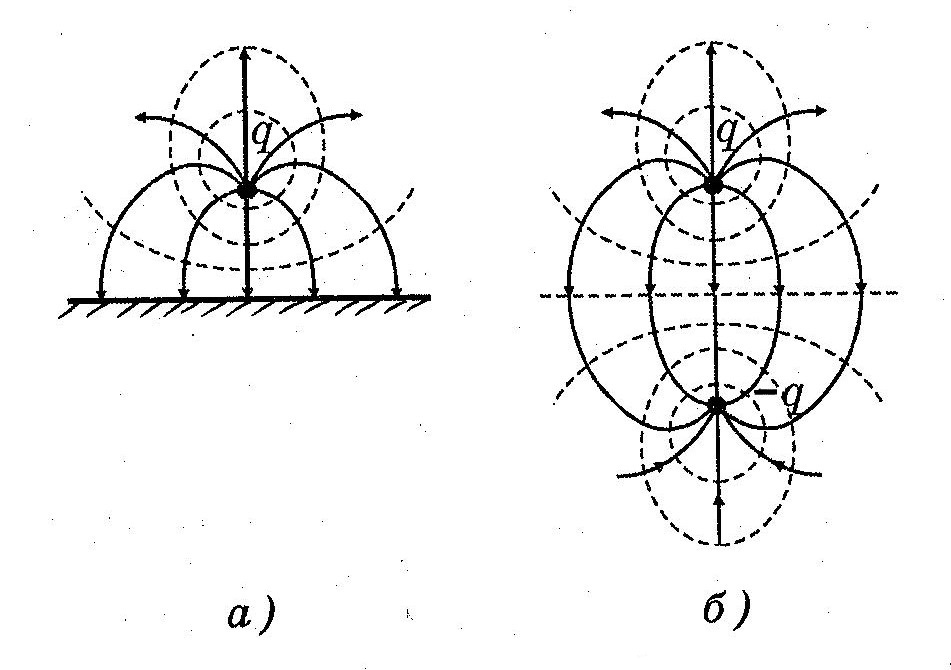 ногда решение - распределение потенциала в пространстве между проводниками - можно угадать. Если угаданное решение удовлетворяет заданным граничным условиям (потенциалам проводников), то оно единственно возможное.

Вот самый простой пример.

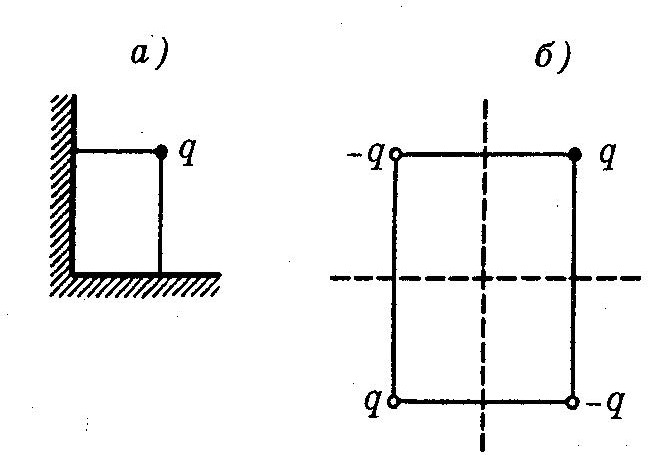
Сравним две ситуации (рис. а, б):

1. точечный заряд находится на расстоянии а от безграничной металлической заземленной пластины;

2. два равных разноименных точечных заряда находятся на расстоянии 2а друг от друга.

В первом случае потенциал на проводящей плоскости равен нулю, а вблизи точечного заряда (который можно рассматривать как предельный случай маленького проводящего шарика радиуса ) потенциал стремиться к бесконечности (точнее, на поверхности этого шарика он принимает значение ).

Во втором случае равен нулю потенциал во всех точках плоскости, расположенной посередине между зарядами, а вблизи зарядов стремится к бесконечности (точнее, принимает значение на поверхностях заряженных шариков).

Так как совпадают значения потенциалов на двух поверхностях (плоской и маленького шарика с зарядом ) в этих ситуациях, то совпадают и поля между этими поверхностями, т.е. в полупространстве сверху от плоскости.

Можно прийти к тому же выводу, рассуждая по-другому. Совместим со средней эквипотенциальной поверхностью двух зарядов (ситуация 2) проводящую плоскость. Эта плоскость может рассматриваться как предельный случай замкнутой сферической оболочки бесконечно большого радиуса. Мы знаем, что две части пространства, разделенные замкнутой проводящей оболочкой, в электрическом отношении независимы друг от друга. Поэтому, если убрать снизу заряд , поле над плоскостью не изменится.

Итак, поле над проводящей безграничной плоскостью такое же, как поле двух равных разноименных зарядов и . Для вычисления напряженности в любой точке над плоскостью мы можем мысленно поместить «заряд-изображение» противоположного знака с другой стороны плоскости симметрично по отношению к заряду . Надо понимать, что реально поле над плоскостью есть результат суперпозиции полей точечного заряда и зарядов противоположного знака, наведенных на плоскости, но в итоге получается такая же конфигурация поля, как и для двух точечных зарядов . (По другую сторону от плоскости электрические поля в этих ситуациях, естественно, различны: в первом случае поле снизу от пластины отсутствует, во втором – нет.)

Теперь мы легко найдем силу взаимодействия заряда с плоскостью, поле в любой точке между ними, распределение индуцированного заряда на плоскости (см. решение задачи 2.32).

Вот еще некоторые задачи, в которых можно использовать метод зеркальных изображений:

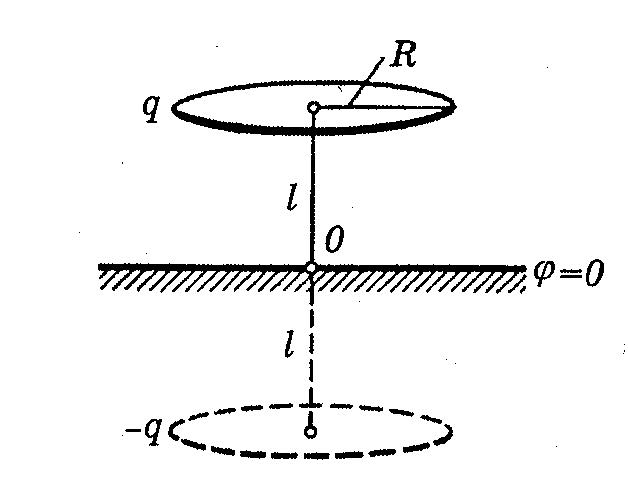
Заряженное кольцо над проводящей плоскостью

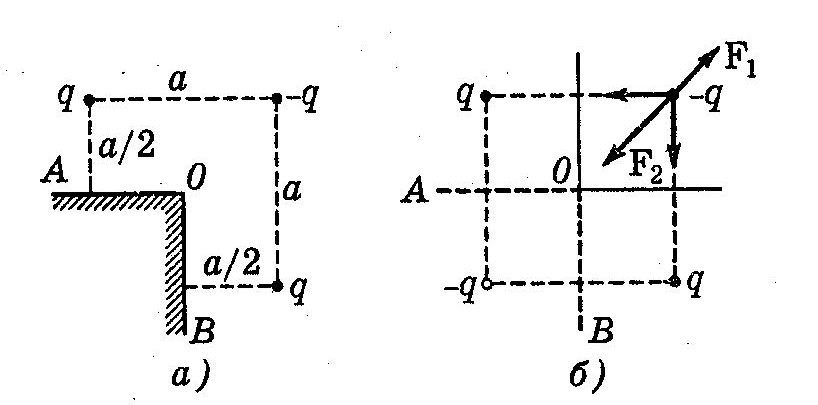
Заряд между двумя проводящими плоскостями; Три заряда над плоскостями