
- •Правила Кірхгофа для розгалужених кіл
- •Правила Кірхгофа для розгалужених кіл:
- •Правила Кірхгофа для розгалужених кіл:
- •Правила Кірхгофа для розгалужених кіл мають вигляд:
- •Правила Кірхгофа для розгалужених кіл записуються так:
- •Правила Кірхгофа для розгалужених кіл записуються так:
- •Правила Кірхгофа для розгалужених кіл записуються так:
- •Спочатку замінимо паралельне з’єднання опорів та на еквівалентне згідно з формулою:
- •Спочатку замінимо паралельне з’єднання опорів та на еквівалентний опір згідно з формулою:
- •Правила Кірхгофа для розгалужених кіл записуються так:
- •Спочатку замінимо паралельне з’єднання опорів та на еквівалентне згідно з формулою:
- •Для визначення струму застосуємо правила Кірхгофа для розгалужених кіл:
- •Для визначення струму застосуємо правила Кірхгофа для розгалужених кіл:
- •Д 3.165 ля визначення струму застосуємо правила Кірхгофа для розгалужених кіл:
3.1.
Два точкових заряди, що знаходячись в
повітрі на відстані
![]() = 20 см один від одного, взаємодіють з
деякою силою. На якій відстані R
треба помістити ці заряди в маслі, щоб
отримати ту ж силу взаємодії?
= 20 см один від одного, взаємодіють з
деякою силою. На якій відстані R
треба помістити ці заряди в маслі, щоб
отримати ту ж силу взаємодії?
3.1.
Дано
= 20 см
![]() = 3
= 3![]()
![]() = ?
= ?
За законом Кулона
сила, з якою взаємодіють два точкових
заряди
![]() і
і
![]() ,
визначається за формулою
,
визначається за формулою
![]() , (1)
, (1)
де r
— відстань між зарядами;
— відносна діелектрична проникність
середовища
![]() = 8,854∙10-12
Ф/м - електрична стала.
= 8,854∙10-12
Ф/м - електрична стала.
Якщо заряди однойменні, то сила, з якою заряд діє на заряд буде:
![]() , (2)
, (2)
де
![]() — радіус-вектор,
проведений від заряду
до заряду
,
— радіус-вектор,
проведений від заряду
до заряду
,
![]() - одиничний
вектор.
- одиничний
вектор.
Запишемо формулу (1) для двох випадків розташування зарядів – у повітрі і маслі:
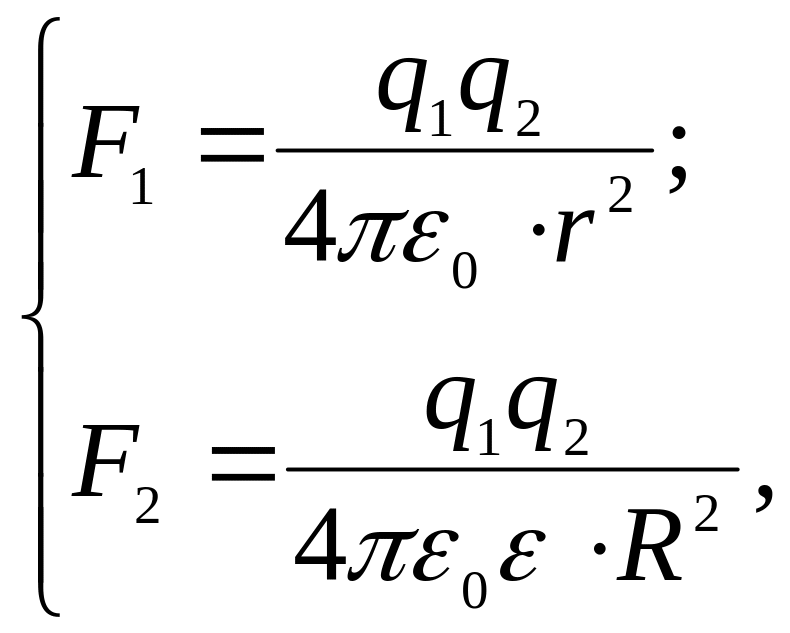 , (3)
, (3)
Порівняємо праві частини рівнянь системи (3) і одержимо вираз для розрахунку відстані R, на якій треба помістити ці заряди в маслі, щоб отримати ту ж силу взаємодії, що і в повітрі:
= (4)
Зробимо підстановку заданих в умові задачі величин у системі СІ у формулу (4) і отримаємо відповідь:
=
3.2. Знайти
напруженість електричного поля
![]() в точці, що лежить посередині між
точковими зарядами q1
= 8 нКл і q2
= 6 нКл. Відстань між зарядами 10 см.
в точці, що лежить посередині між
точковими зарядами q1
= 8 нКл і q2
= 6 нКл. Відстань між зарядами 10 см.
3.2.
Дано
= 10 см
= 3 q1
= 8 нКл q2
= 6 нКл
= ?
Рис. 3.2
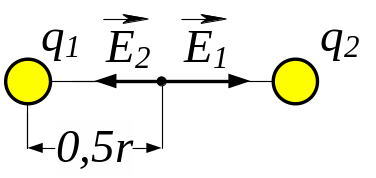
Напруженість електричного поля
![]() , (1)
, (1)
З означення
напруженості випливає, що, коли внести
в якусь точку електричного поля частинку,
заряд якої
![]() ,
то на цю
частинку діятиме сила
,
то на цю
частинку діятиме сила
![]() ,
(2)
,
(2)
де
![]() - вектор
напруженості в цій точці поля.
- вектор
напруженості в цій точці поля.
Напруженість поля, яке створене точковим зарядом:
![]() ;
у векторній формі
;
у векторній формі
![]() ,
(3)
,
(3)
де
![]() = 9∙109
м/Ф – коефіцієнт пропорційності; r
— відстань між зарядами;
— відносна діелектрична проникність
середовища
= 8,854∙10-12
Ф/м - електрична стала.
= 9∙109
м/Ф – коефіцієнт пропорційності; r
— відстань між зарядами;
— відносна діелектрична проникність
середовища
= 8,854∙10-12
Ф/м - електрична стала.
За принципом незалежності дії сил рівнодійна сила дорівнює геометричній сумі складових, тобто
![]() . (4)
. (4)
Тоді можна стверджувати, що виконується така рівність:
![]() , (5)
, (5)
тобто напруженість електричного поля декількох зарядів дорівнює геометричній сумі напруженості, яку створюють кожний з зарядів окремо. Згідно з рис. 3.2 загальна напруженість поля дорівнює різниці напруженості поля першого і другого зарядів і направлена в сторону другого заряду. Запишемо ці напруженості для заданої точки поля:
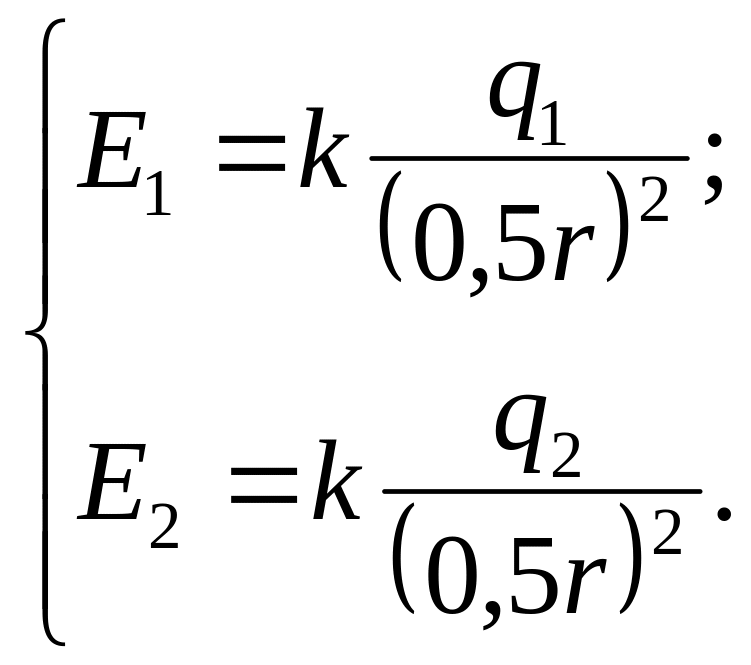 (6)
(6)
Напруженість електричного поля в точці, що лежить посередині між точковими зарядами згідно з формулами (5) та (6) дорівнюватиме
![]() . (7)
. (7)
Зробимо підстановку заданих в умові задачі величин (у системі СІ) у формулу (7) і отримаємо відповідь:
=
3
Рис. 3.3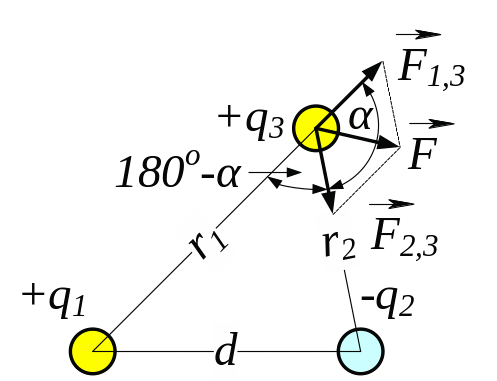
![]() = 10 см. Визначити силу, яка діє на заряд
Q3
=1 мкКл, що відстоїть па відстані
= 10 см. Визначити силу, яка діє на заряд
Q3
=1 мкКл, що відстоїть па відстані
![]() = 12 см від заряду Q1
і на відстані
= 12 см від заряду Q1
і на відстані
![]() = 10 см від заряду Q2.
= 10 см від заряду Q2.
3.3.
Дано
Q1
= 100 нКл
Q2
= - 50 нКл
= 10 см
= 1 Q3
=1 мкКл
= 12 см
= 10 см
![]() = ?
= ?
За законом Кулона сила, з якою взаємодіють два точкових заряди і , визначається за формулою
, (1)
де r — відстань між зарядами; — відносна діелектрична проникність середовища; = 8,854∙10-12 Ф/м - електрична стала.
Якщо заряди однойменні, то сила, з якою заряд діє на заряд буде:
, (2)
де — радіус-вектор, проведений від заряду до заряду , - одиничний вектор.
Запишемо формулу (1) для двох випадків взаємодії зарядів: між першим і третім та між другим і третім:
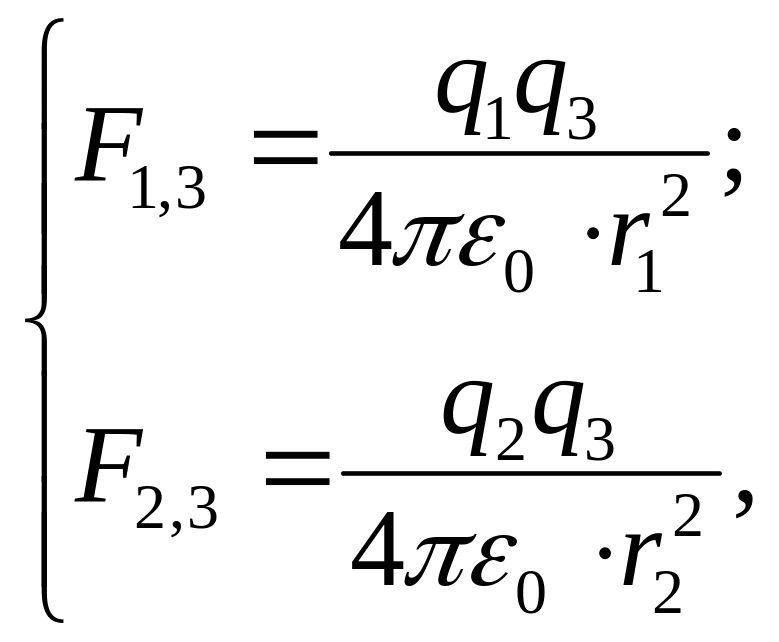 , (3)
, (3)
Згідно рис. 3.3, сили
з системи (3) напрямлені під кутом
![]() друг відносно другого, тому їхній добуток
знаходимо за формулою косинусів:
друг відносно другого, тому їхній добуток
знаходимо за формулою косинусів:
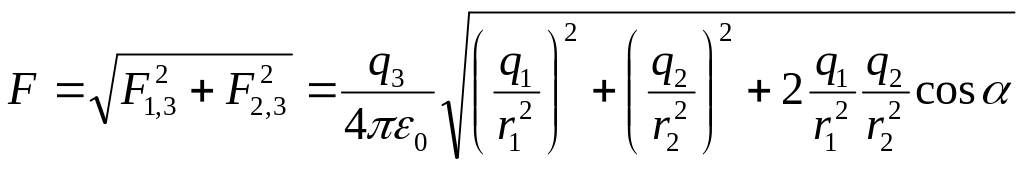 . (4)
. (4)
Величину
![]() визначимо з трикутника
визначимо з трикутника
![]() ,
до якого застосуємо теорему косинусів:
,
до якого застосуємо теорему косинусів:
![]() . (5)
. (5)
Отриману величину з формули (5) підставляємо в вираз (4) і отримаємо вираз для розрахунку відповіді:
= (6)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (6) і отримаємо відповідь:
=
3.4. Довгий
прямий тонкий дріт несе рівномірно
розподілений заряд. Обчислити лінійну
густину
![]() заряду, якщо напруженість поля на
відстані
заряду, якщо напруженість поля на
відстані
![]() = 0,5 м від дроту проти його середини
складає Е
= 2 В/см.
= 0,5 м від дроту проти його середини
складає Е
= 2 В/см.
Розв’язок.
Т
Рис. 3.4
Дано
= 0,5 м
Е
= 2 В/см
= ?
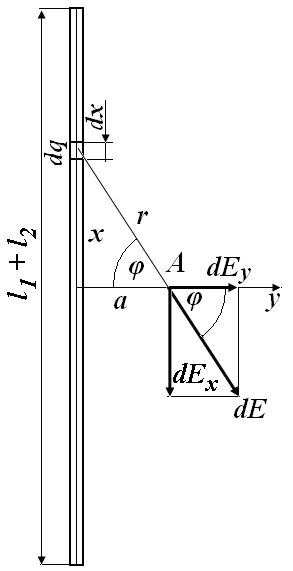
![]() .
(1)
.
(1)
Шукана напруженість
поля в точці А
дорівнює сумі елементарних напруженості
![]() ,
створених в цій точці усіма елементами
стержня, які мають різний напрям. Отже,
їх векторна сума не дорівнює сумі їх
модулів і не може бути виражена інтегралом
,
створених в цій точці усіма елементами
стержня, які мають різний напрям. Отже,
їх векторна сума не дорівнює сумі їх
модулів і не може бути виражена інтегралом
![]() .
.
При цьому, як видно з рис.3.4, проекції вектора на координатні вісі дорівнюють
![]() (2)
(2)
Визначимо dx, для цього диференціюємо вираз
![]() ,
,
і отримаємо
![]() . (3)
. (3)
Підставимо в (2) вирази з (1) і (3)
![]() (4)
(4)
Таким чином, ми
звели завдання до складання однаково
спрямованих векторів
![]() і
і
![]() ,
,
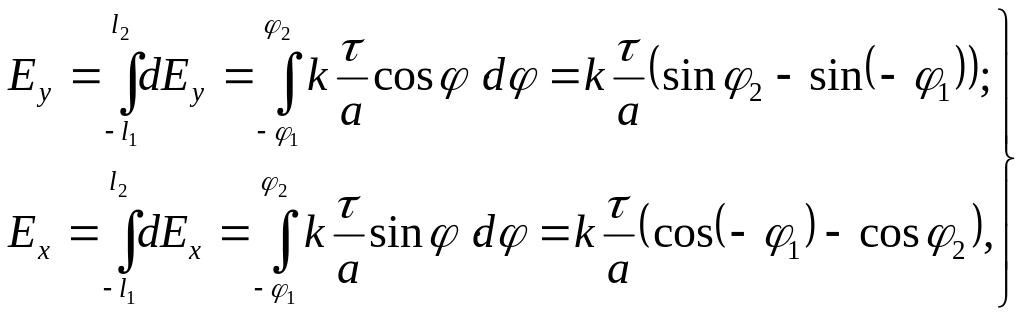 (5).
(5).
де
![]() ,
,
![]() - кути, під якими видно кінці стержня з
точки, в якій визначається напруженість
поля:
- кути, під якими видно кінці стержня з
точки, в якій визначається напруженість
поля:
![]() (6)
(6)
а шукана напруженість виразиться формулою теореми Піфагора
![]() . (7)
. (7)
Підставивши в (7) значення величин з (5), отримаємо
![]() . (8)
. (8)
Тепер розглянемо окремі випадки завдання.
Точка А лежить проти середини стержня, тобто
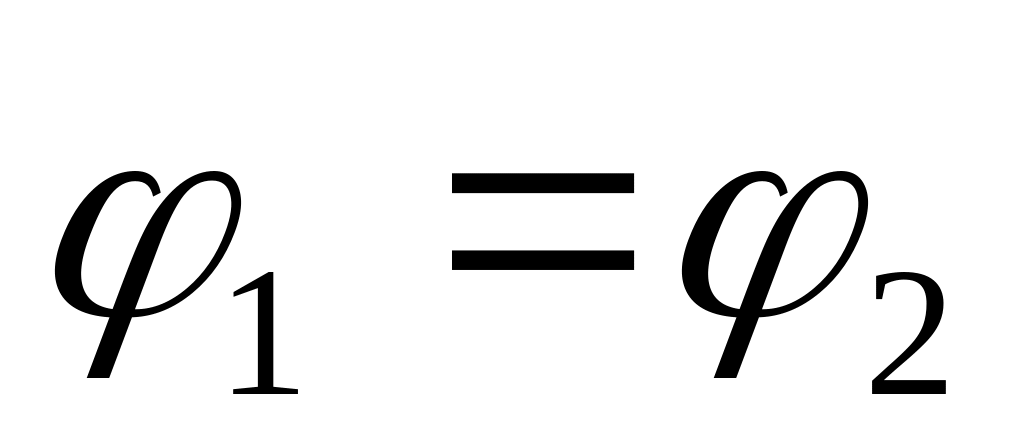 ,
тоді маємо
,
тоді маємо
![]() . (9)
. (9)
2. Нерівність а
>>2![]() (
(![]() )
означає, що можна знехтувати розмірами
стержня порівняно з відстанню від нього
до цієї точки, тобто, заряд стержня можна
вважати точковим. Тоді знайдемо
)
означає, що можна знехтувати розмірами
стержня порівняно з відстанню від нього
до цієї точки, тобто, заряд стержня можна
вважати точковим. Тоді знайдемо
![]() .
(10)
.
(10)
3. З нерівності а
<<
2
випливає, що ця точка знаходиться поблизу
тонкого стержня і далеко від його кінців.
Це відповідає нескінченно довгому
стержню (нитки, циліндру), коли
![]() .
Отже маємо
.
Отже маємо
![]() . (11)
. (11)
З формули (11) визначаємо вираз для розрахунку відповіді:
= (12)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (12) і отримаємо відповідь:
=
3.5. В центр квадрата, в кожній вершині якого знаходиться заряд q = 2,33 нКл, вміщений негативний заряд q0. Знайти цей заряд, якщо результуюча сила, що діє на кожний заряд q, дорівнює нулю.
3.5.
Дано
q
= 2,33 нКл
q0
= ?
За законом Кулона сила, з якою взаємодіють два точкових заряди і , визначається за формулою
, (1)
де r — відстань між зарядами; — відносна діелектрична проникність середовища; = 8,854∙10-12 Ф/м - електрична стала.
Я
Рис. 3.5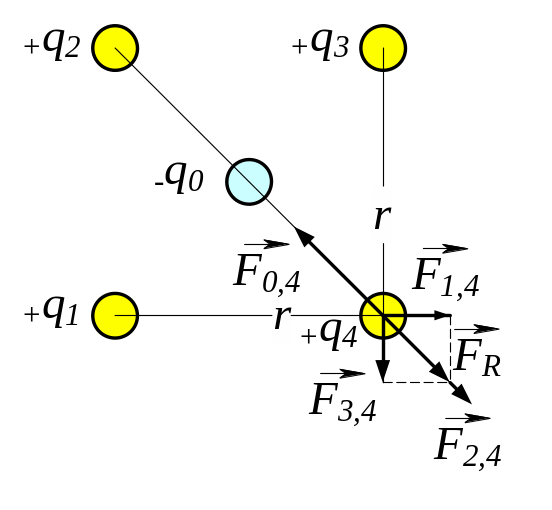
, (2)
де — радіус-вектор, проведений від заряду до заряду , - одиничний вектор.
Запишемо формулу (1) для всіх випадків взаємодії зарядів:
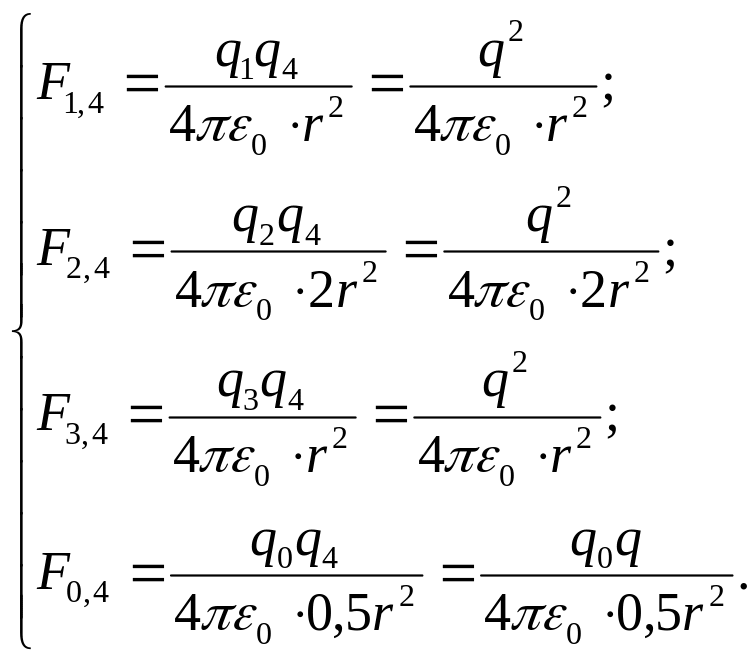 , (3)
, (3)
Згідно рис. 3.5, сили
![]() і
і
![]() з системи (3) напрямлені під кутом 90о
друг відносно другого, тому їхній добуток
знаходимо за формулою:
з системи (3) напрямлені під кутом 90о
друг відносно другого, тому їхній добуток
знаходимо за формулою:
![]() . (4)
. (4)
З рис. 3.5 видно, що повинна виконуватися рівність:
![]() . (5)
. (5)
Розв’язуємо рівняння (5) відносно шуканого заряду і отримаємо рівняння
q0 = (6)
Зробимо підстановку заданих в умові задачі величин у формулу (6) і отримаємо відповідь:
q0 =
3.6. Два
точкових заряди q1
= 7,5 нКл і q2
= - 14,7 нКл розташовані на відстані
= 5 см. Знайти напруженість
електричного поля в точці, що знаходиться
на відстанях
![]() = 3 см від позитивного заряду і
= 3 см від позитивного заряду і
![]() = 4 см від негативного заряду.
= 4 см від негативного заряду.
3.6.
Дано
q1
= 7,5 нКл
q2
= - 14,7 нКл
= 5 см
= 1
= 3 см
= 4 см
= ?
(1)
В
Рис. 3.6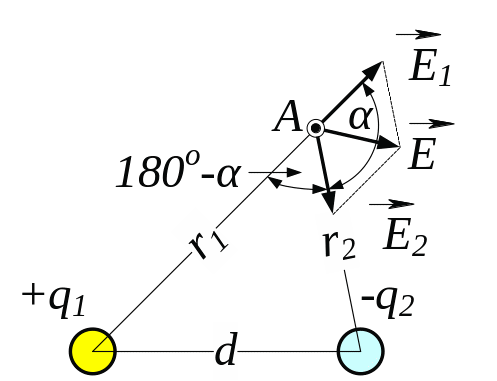
![]() і
і
![]() полів, що утворюється кожним зарядом
окремо:
полів, що утворюється кожним зарядом
окремо:![]() .
Напруженості електричного поля, що
утворюється в повітрі (
= 1) зарядами
і
,
.
Напруженості електричного поля, що
утворюється в повітрі (
= 1) зарядами
і
,
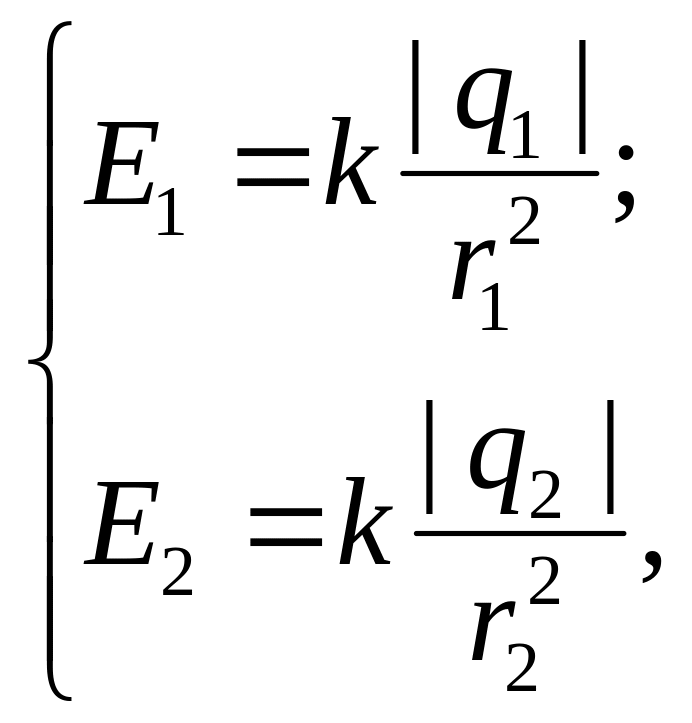 (1)
(1)
Вектор
![]() (рис. 3.6) спрямований по силовій лінії
від заряду
(рис. 3.6) спрямований по силовій лінії
від заряду
![]() ,
тому що цей заряд позитивний; вектор
,
тому що цей заряд позитивний; вектор
![]() спрямований також по силовій лінії, але
до заряду
спрямований також по силовій лінії, але
до заряду
![]() ,
тому що цей заряд негативний.
,
тому що цей заряд негативний.
Модуль вектора знайдемо за теоремою косинусів:
![]() , (2)
, (2)
де
- кут між векторами
![]() і
і
![]() ,
який можемо знайти із трикутника зі
сторонами
,
який можемо знайти із трикутника зі
сторонами
![]() і
і
![]()
![]() . (3)
. (3)
Підставляючи вираз
![]() і
і
![]() із (1), косинуса з (3) у (2) і виносячи спільний
множник 1/(4л
із (1), косинуса з (3) у (2) і виносячи спільний
множник 1/(4л![]() )
за знак кореня, одержуємо
)
за знак кореня, одержуємо
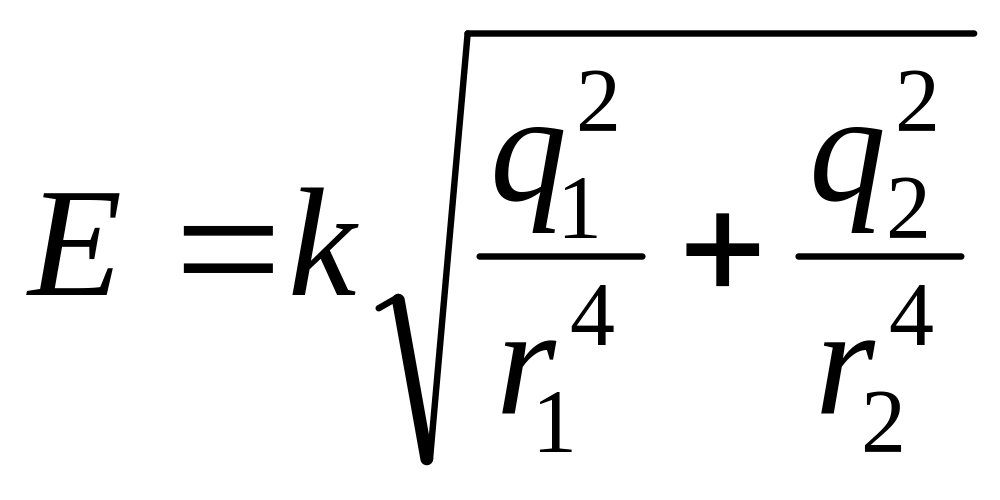 (4)
(4)
Зробимо підстановку заданих в умові задачі величин у формулу (4) і отримаємо відповідь:
=
3.7. Дві кульки однакових радіуса і маси підвішені на нитках однакової довжини так, що їх поверхні стикаються. Після надання кулькам заряду q = 0,4 мкКл вони відштовхнулися одна від одної і розійшлися на кут = 60°. Знайти масу кульки, якщо відстань від центра кульки до точки її підвісу = 20 см.
Рис. 3.7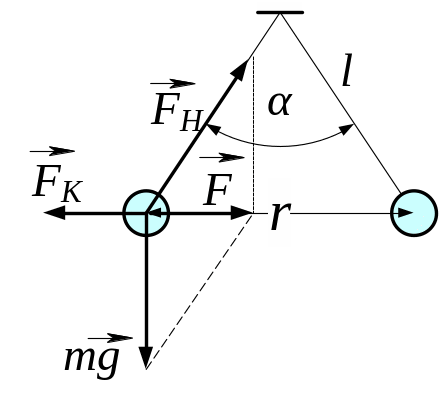
3.7.
Дано
q
= 0,4 мкКл
= 60°
= 20 см
![]() = ?
= ?
За законом Кулона сила, з якою взаємодіють два точкових заряди і , визначається за формулою
, (1)
де r — відстань між зарядами; — відносна діелектрична проникність середовища; = 8,854∙10-12 Ф/м - електрична стала.
Якщо заряди однойменні, то сила, з якою заряд діє на заряд буде:
, (2)
де — радіус-вектор, проведений від заряду до заряду , - одиничний вектор.
Запишемо формулу (1) для нашого випадку взаємодії однакових зарядів:
![]() , (3)
, (3)
де
![]() оскільки трикутних складений нитками
рівносторонній.
оскільки трикутних складений нитками
рівносторонній.
Згідно рис. 3.7, сили
![]() і
зрівноважують одна одну тому заряди
знаходяться в рівновазі. Останню силу
визначаємо з прямокутного трикутника
і отримуємо рівняння:
і
зрівноважують одна одну тому заряди
знаходяться в рівновазі. Останню силу
визначаємо з прямокутного трикутника
і отримуємо рівняння:
![]() , (4)
, (4)
З рівняння (4) отримуємо вираз для розрахунку маси кульки:
= (5)
Зробимо підстановку заданих в умові задачі величин у формулу (5) і отримаємо відповідь:
=
3.8. Дві
кульки однакових радіуса і маси підвішені
на нитках однакової довжини так, що їх
поверхні стикаються. Який заряд q
треба надати кулькам, щоб сила натягу
ниток стала рівною
![]() = 98 мН? Відстань від центра кульки до
точки її підвісу
= 10 см; маса кожної кульки m
= 5 г.
= 98 мН? Відстань від центра кульки до
точки її підвісу
= 10 см; маса кожної кульки m
= 5 г.
3
Рис. 3.8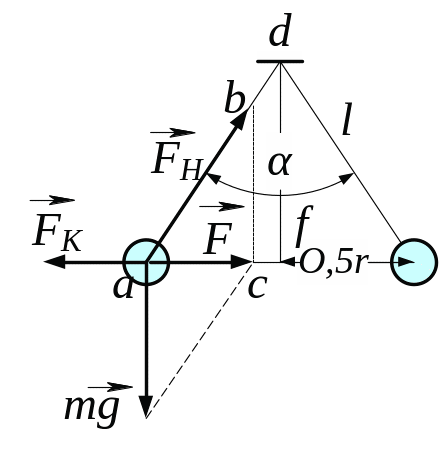
Дано
= 98 мН
= 10 см
= 5 г
= ?
З рис. 3.8 випливає, що кулі будуть в рівновазі, якщо буде виконуватись рівність:
![]() , (1)
, (1)
За законом Кулона сила, з якою взаємодіють два точкових заряди і , визначається за формулою
, (2)
де r — відстань між зарядами; — відносна діелектрична проникність середовища; = 8,854∙10-12 Ф/м - електрична стала.
Якщо заряди однойменні, то сила, з якою заряд діє на заряд буде:
, (3)
де — радіус-вектор, проведений від заряду до заряду , - одиничний вектор.
Запишемо формулу (2) для нашого випадку взаємодії однакових зарядів:
, (4)
де
визначаємо з подібності прямокутних
трикутників
![]() і
і
![]() :
:
![]() , (5)
, (5)
З трикутника сил та формул (1), (4) та (5) отримаємо
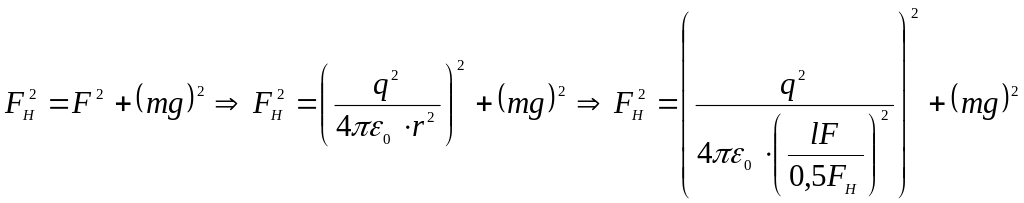 . (6)
. (6)
З рівняння (6) отримуємо вираз для розрахунку заряду куль:
= (7)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (5) і отримаємо відповідь:
=
3.9. До зарядженої нескінченної площини з поверхневою густиною заряду σ = 40 мкКл/м2, підвішена однойменно заряджена кулька масою = 1 г і зарядом q = 1 нКл. Який кут ß з нескінченною площиною утворить нитка, на якій висить кулька?
3
Рис. 3.9
Дано
σ
= 40 мкКл/м2
= 1 г q
= 1 нКл
![]() = ?
= ?
З рис. 3.9 випливає, що куля буде в рівновазі, якщо буде виконуватись рівність:
, (1)
За законом Кулона сила, з якою взаємодіє точковий заряди з зарядженою поверхнею, визначається за формулою
![]() , (2)
, (2)
де — напруженість електричного поля створеного зарядженою нескінченною площиною, яку визначаємо за формулою
![]() , (3)
, (3)
Кут визначаємо з трикутника сил:
![]() , (4)
, (4)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (4) і отримаємо відповідь:
=
3.10. До зарядженої нескінченної площини, підвішена однойменно заряджена кулька масою 0,4 мг і зарядом q = 667 пКл. Сила натягу нитки, на якій висить кулька, = 0,49 мН. Знайти поверхневу густину заряду σ на площині.
3
Рис. 3.10
Дано
= 0,4 мг q
= 667 пКл
= 0,49 мН
![]() = ?
= ?
З рис. 3.10 випливає, що куля буде в рівновазі, якщо буде виконуватись рівність:
. (1)
За законом Кулона сила, з якою взаємодіє точковий заряди з зарядженою поверхнею, визначається за формулою
, (2)
де — напруженість електричного поля створеного зарядженою нескінченною площиною, яку визначаємо за формулою
![]() . (3)
. (3)
Силу знаходимо з прямокутного трикутника сил за теоремою Піфагора:
![]() . (4)
. (4)
Знаходимо поверхневу густину заряду σ з формули (4):
= (5)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (5) і отримаємо відповідь:
= =
3.11. Дві довгі однойменно заряджені нитки розташовані на відстані = 10 см одна від одної. Лінійна густина заряду на нитках = 10 мкКл/м. Знайти модуль напруженості електричного поля в точці, що знаходиться на відстані = 10 см від кожної з ниток.
Рис. 3.11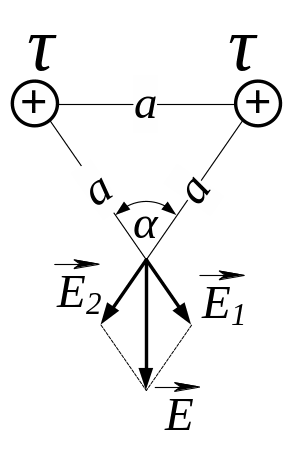
3.11.
Дано
= 10 см
= 10 мкКл/м
= ?
Лінійна густина заряду дорівнює
![]() . (1)
. (1)
Якщо точка лежить
проти середини нитки, тобто
![]() =
=
![]() ;
в) нескінченно довгого прямого рівномірно
зарядженого циліндра:
;
в) нескінченно довгого прямого рівномірно
зарядженого циліндра:
![]() , (2)
, (2)
де - лінійна густина заряду; а - відстань від нитки до точки, в якій визначається напруженість; - кути, під якими видно кінці нитки з точки, в якій визначається напруженість поля.
З рис. 3.11 випливає, що модуль напруженості поля, яке створене двома зарядженими нитками визначаємо за формулою теореми косинусів:
![]() . (3)
. (3)
Значення = 0,5 знаходимо з трикутника (див. рис. 3.11) та разом з величинами, які задані в умові задачі, підставляємо у формулу (3) і отримаємо відповідь:
=
3.12. Мідна куля радіусом = 0,5 см занурена в масло. Густина масла ρ = 0,8 103 кг/м3. Знайти заряд кулі, якщо в однорідному електричному полі вона виявилася зрівноваженою в маслі. Електричне поле направлене вертикально вгору і його напруженість = 3,6 МВ/м.
Рис. 3.12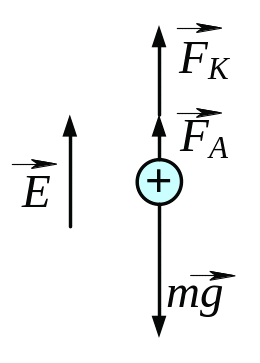
3.12.
Дано
= 0,5 см ρ
= 0,8 103
кг/м3
= 3,6 МВ/м.
= ?
![]() = 8,6∙103
кг/м3
= 8,6∙103
кг/м3
З рис. 3.12 видно, що куля буде в рівновазі, якщо буде виконуватись рівність модулів сил:
![]() . (1)
. (1)
За законом Кулона сила, з якою взаємодіє точковий заряди з електричним полем, визначається за формулою
, (2)
де — напруженість електричного.
Силу
![]() знаходимо за формулою закону Архімеда:
знаходимо за формулою закону Архімеда:
![]() . (3)
. (3)
Вагу кулі визначаємо за формулою:
![]() . (4)
. (4)
Значення сил з формул (2), (3) та (4) підставляємо в формулу (1):
![]() . (5)
. (5)
Заряд кулі знаходимо з формули (5):
= (6)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (6) і отримаємо відповідь:
=
3.13. В плоскому горизонтально розташованому конденсаторі заряджена капелька ртуті знаходиться в рівновазі при напруженості електричного поля = 60 кВ/м. Заряд каплі = 0,8 нКл. Знайти її радіус.
3.13.
Дано
= 60 кВ/м
= 0,8 нКл
= ?
Рис. 3.13
![]() = 13,6∙103
кг/м3
= 13,6∙103
кг/м3
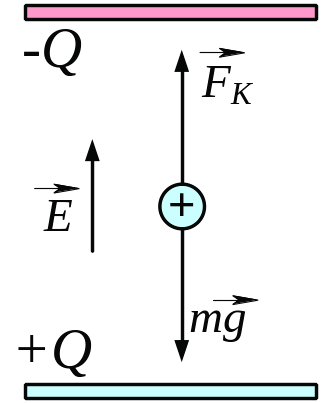
З рис. 3.13 видно, що куля буде в рівновазі, якщо буде виконуватись рівність модулів сил:
![]() . (1)
. (1)
За законом Кулона сила, з якою взаємодіє точковий заряди з електричним полем, визначається за формулою
, (2)
де — напруженість електричного в конденсаторі.
Вагу кулі визначаємо за формулою:
. (3)
Значення сил з формул (2) та (3) підставляємо в формулу (1):
![]() . (4)
. (4)
Радіус кулі знаходимо з формули (4):
= (6)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (6) і отримаємо відповідь:
=
3.14. Дві кульки масою = 1 г кожна, підвішені на нитках, верхні кінці яких з'єднані. Довжина кожної нитки = 10 см. Які однакові заряди треба надати кулькам, щоб нитки розійшлися на кут α = 60°?
3
Рис. 3.8
Дано
= 10 см
= 1 г α
= 60°
= ?
З рис. 3.8 випливає, що кулі будуть в рівновазі, якщо буде виконуватись рівність:
, (1)
За законом Кулона сила, з якою взаємодіють два точкових заряди і , визначається за формулою
, (2)
де r — відстань між зарядами; — відносна діелектрична проникність середовища; = 8,854∙10-12 Ф/м - електрична стала.
Якщо заряди однойменні, то сила, з якою заряд діє на заряд буде:
, (3)
де — радіус-вектор, проведений від заряду до заряду , - одиничний вектор.
Запишемо формулу (2) для нашого випадку взаємодії однакових зарядів:
![]() , (4)
, (4)
де
![]() бо трикутник рівносторонній.
бо трикутник рівносторонній.
Силу , яка протидіє силі Кулона, знаходимо з прямокутного трикутника сил за формулою
![]() . (5)
. (5)
Сили з рівнянь (4) та (5) підставляємо у формулу (1) і отримуємо вираз для розрахунку заряду куль:
= (6)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (6) і отримаємо відповідь:
=
3.15. Точкові заряди Q1 = 20 мкКл, та Q2 = - 10 мкКл знаходяться на відстані = 5 см один від одного. Визначити напруженість поля в точці, що знаходиться на відстані = 3 см від першого і на відстані = 4 см від другого заряду. Визначити також силу F, що діє в цій точці на точковий заряд Q = 1 мкКл.
3.15.
Рис. 3.15
Дано
Q1
= 20 мкКл Q2
= - 10 мкКл
= 5 см
= 1
= 3 см
= 4 см Q
= 1 мкКл
= ?
= ?
Відповідно до
принципу суперпозиції електричних
полів, кожний заряд створює поле незалежно
від присутності в просторі інших зарядів.
Тому напруженість
електричного поля в шуканій точці може
бути знайдена як геометрична сума
напруженості
і
полів, що утворюється кожним зарядом
окремо:
.
Напруженості електричного поля, що
утворюється в повітрі (
= 1) зарядами
![]() і
і
![]() ,
,
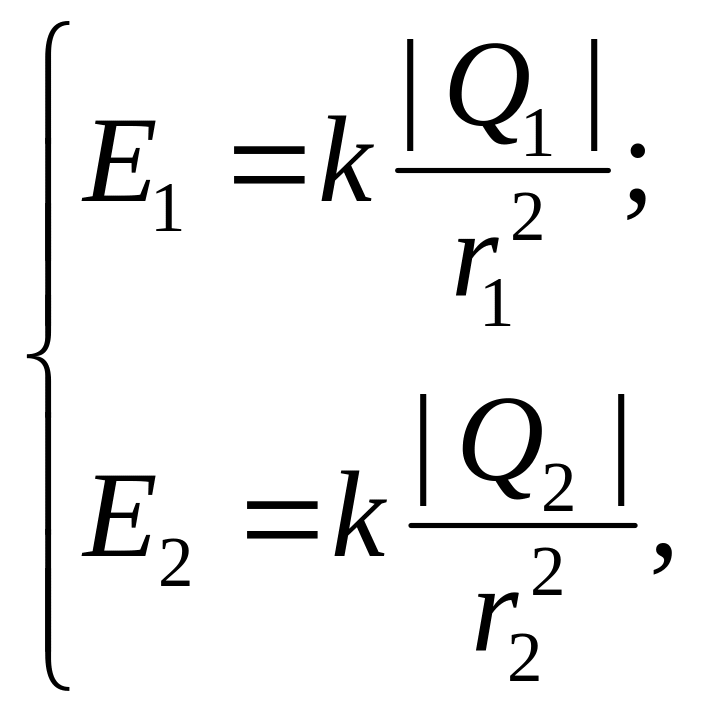 (1)
(1)
Вектор (рис. 3.15) спрямований по силовій лінії від заряду , тому що цей заряд позитивний; вектор спрямований також по силовій лінії, але до заряду , тому що цей заряд негативний.
Модуль вектора знайдемо за теоремою косинусів:
, (2)
де - кут між векторами і , косинус якого можемо знайти із трикутника зі сторонами і
. (3)
Підставляючи вираз і із (1), косинуса з (3) у (2) і виносячи спільний множник 1/(4л ) за знак кореня, одержуємо
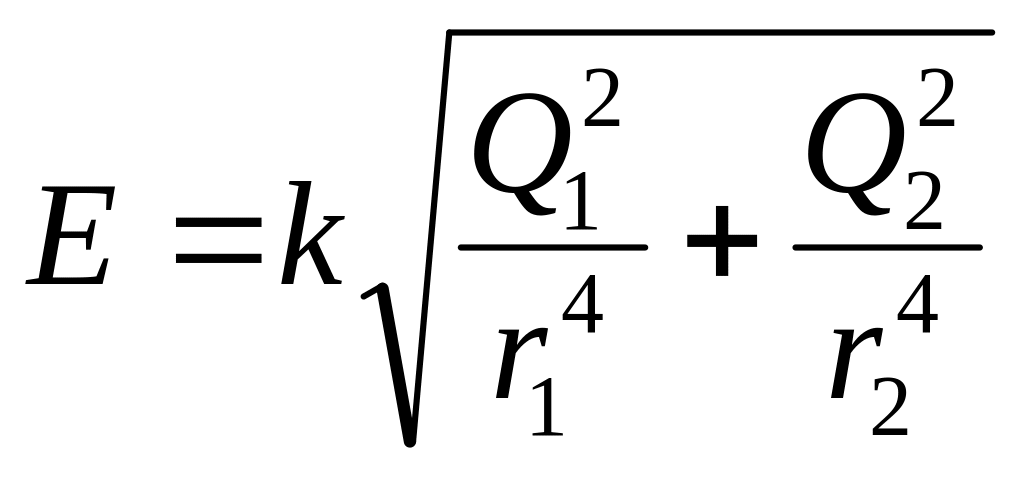 (4)
(4)
Силу, що діє в цій
точці поля на заряд
![]() знаходимо за формулою напруженості
поля:
знаходимо за формулою напруженості
поля:
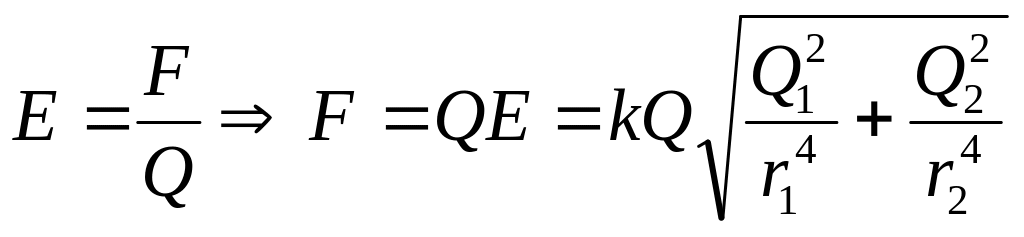 (5)
(5)
Зробимо підстановку заданих в умові задачі величин у формули (4) та (5) і отримаємо відповіді:
= =
3.16. Три однакових точкових заряди Q1 = Q2 = Q3 = 2 нКл знаходяться у вершинах рівностороннього трикутника зі сторонами а = 10 см. Визначити модуль сили , що діє на один із зарядів з боку двох інших.
Рис. 3.16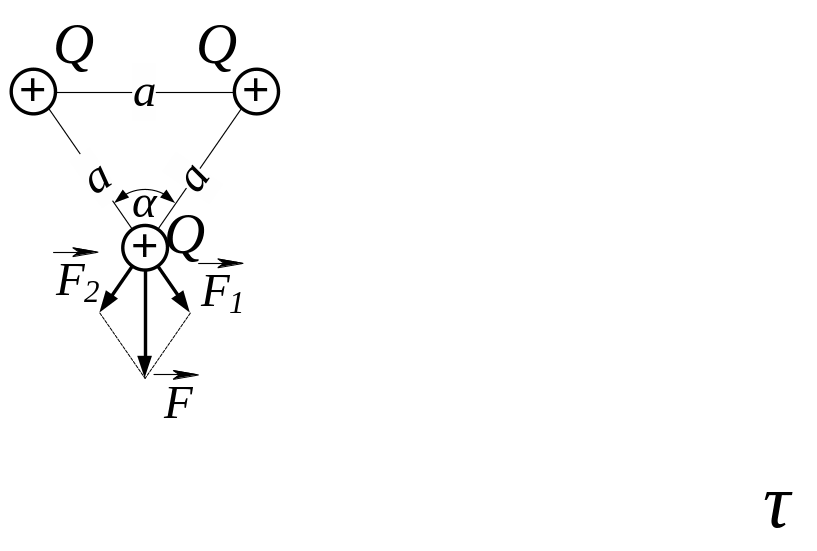
3.16.
Дано
= 10 см
= 10 мкКл/м
= ?
Відповідно до принципу суперпозиції електричних полів, кожний заряд створює поле незалежно від присутності в просторі інших зарядів. Тому напруженість електричного поля в шуканій точці може бути знайдена як геометрична сума напруженості і полів, що утворюється кожним зарядом окремо: . Напруженості електричного поля, що утворюється в повітрі ( = 1) зарядами і ,
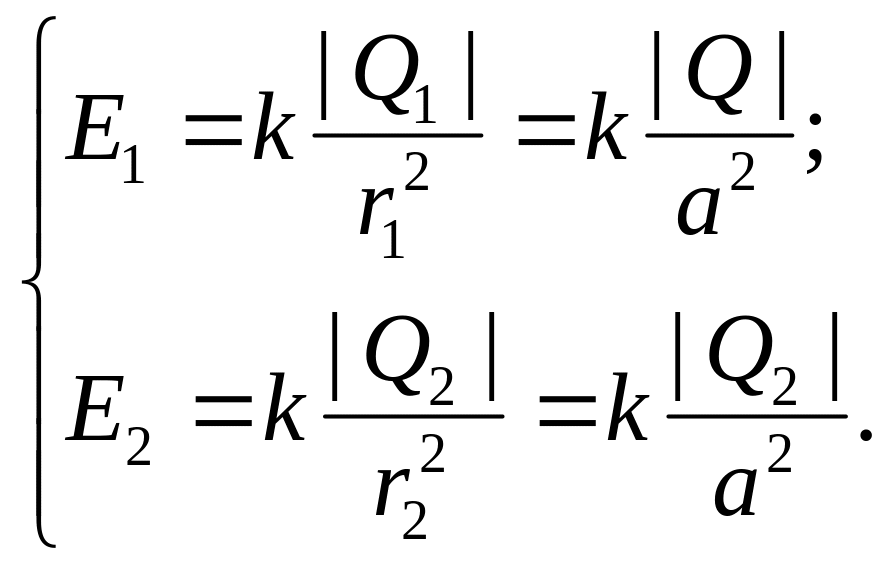 (1)
(1)
Вектор (рис. 3.16) спрямований по силовій лінії від заряду , тому що цей заряд позитивний; вектор спрямований також по силовій лінії, але до заряду , тому що цей заряд негативний.
Модуль вектора знайдемо за теоремою косинусів:
, (2)
де - кут між векторами і , косинус якого можемо знайти із трикутника зі сторонами і
![]() . (3)
. (3)
Підставляючи вираз і із (1), косинуса з (3) у (2) і виносячи спільний множник 1/(4л ) за знак кореня, одержуємо
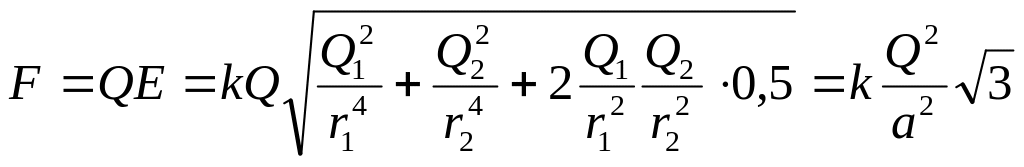 (4)
(4)
Зробимо підстановку заданих в умові задачі величин у формулу (4) і отримаємо відповідь:
=
3.17. Два позитивних точкових заряди = Q і = 9Q закріплені на відстані = 100 см один від одного. Визначити на якій відстані Від заряду Q, треба помістити третій заряд так, щоб він знаходився в рівновазі.
3.17.
Дано
= Q
= 9Q
= 100 см
![]() = ?
= ?
З
Рис. 3.17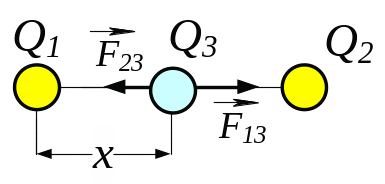
![]() , (1)
, (1)
За законом Кулона сила, з якою взаємодіють два точкових заряди і , визначається за формулою
, (2)
де r — відстань між зарядами; — відносна діелектрична проникність середовища; = 8,854∙10-12 Ф/м - електрична стала.
Якщо заряди однойменні, то сила, з якою заряд діє на заряд буде:
, (3)
де — радіус-вектор, проведений від заряду до заряду , - одиничний вектор.
Запишемо формулу (2) для нашого випадку взаємодії точкових зарядів:
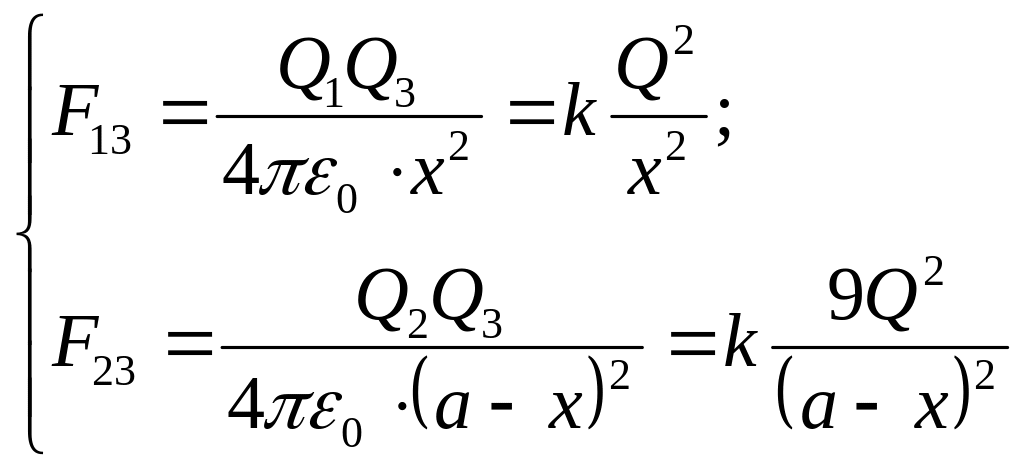 , (4)
, (4)
З виразу (1) отримуємо рівняння:
![]() , (5)
, (5)
Розв’язок рівняння (5) дає вираз для розрахунку відстані
=. (6)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (6) і отримаємо відповідь:
=
3.18. Дві однаково заряджені кульки підвішені на нитках однакової довжини. При цьому нитки розійшлися на деякий кут . Кульки занурюють в олію. Чому дорівнює густина олії, якщо кут на який розійшлися нитки при цьому не змінився? Густина матеріалу кульок ρ0 = 1,5 103 кг/м3, діелектрична проникність олії ε = 2,2.
3
Рис. 3.18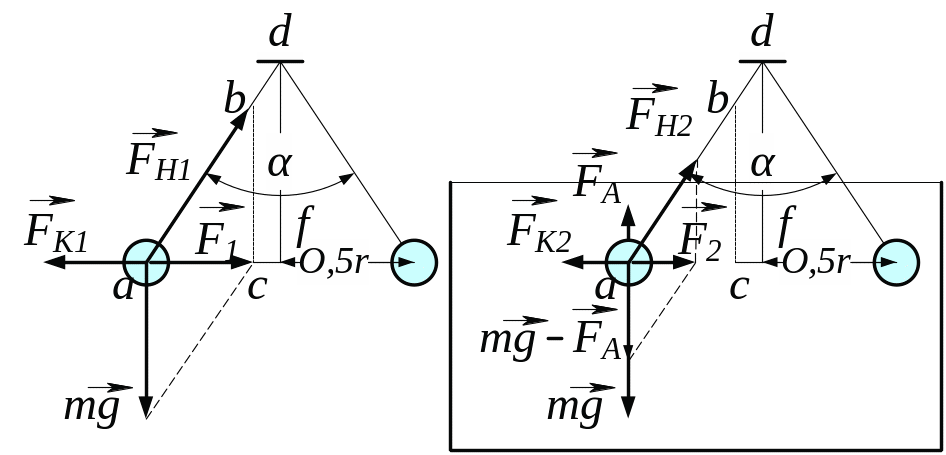
Дано
ρ0
= 1,5 103
кг/м3 ε
= 2,2
![]() = ?
= ?
З рис. 3.18 випливає, що кулі будуть в рівновазі, якщо буде виконуватись рівність:
, (1)
За законом Кулона сила, з якою взаємодіють два точкових заряди і , визначається за формулою
, (2)
де r — відстань між зарядами; — відносна діелектрична проникність середовища; = 8,854∙10-12 Ф/м - електрична стала.
Якщо заряди однойменні, то сила, з якою заряд діє на заряд буде:
, (3)
де — радіус-вектор, проведений від заряду до заряду , - одиничний вектор.
Запишемо формулу (2) для нашого випадку взаємодії однакових зарядів, але в різній речовині:
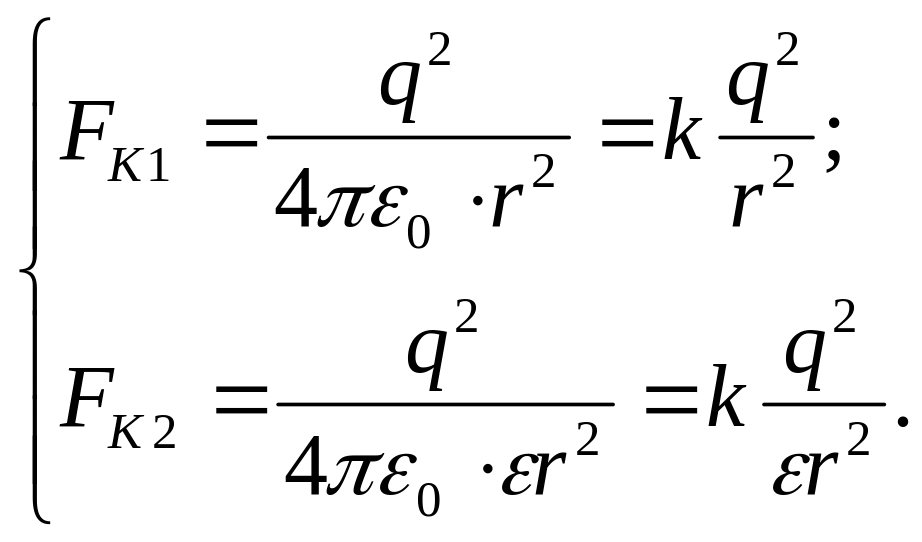 , (4)
, (4)
Силу , яка протидіє силі Кулона, знаходимо з прямокутного трикутника сил за формулою
![]() . (5)
. (5)
Сили з рівнянь (4) та (5) порівнюємо з урахуванням виразу (1) і знаходимо відношення отриманих рівнянь:
![]() = (6)
= (6)
Розв’язуємо отримане рівняння (7) відносно густини речовини
![]() = (7)
= (7)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (7) і отримаємо відповідь:
=
3.19. Чотири однакових заряди 1 = 2 = 3 = 4 = = 40 нКл закріплені у вершинах квадрата зі стороною = 10 см. Знайти силу F, що діє на один з цих зарядів з боку трьох інших.
Рис. 3.19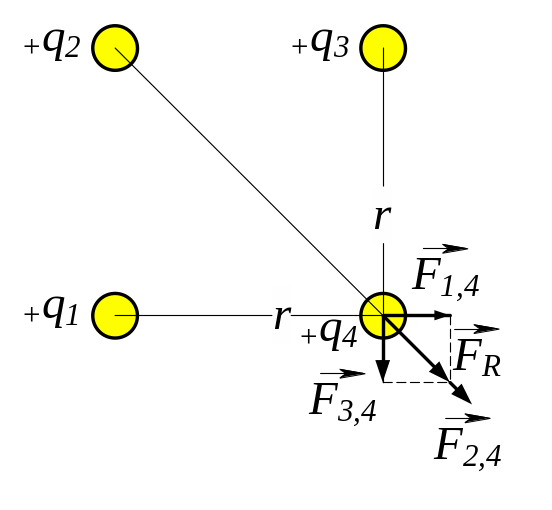
3.19.
Дано
1
=
2
=
3
=
=
4
=
= 40 нКл
= 10 см
= ?
З рис. 3.19 випливає, що шукана сила дорівнює векторній сумі сил, які діють, наприклад, на четвертий заряд:
![]() , (1)
, (1)
За законом Кулона сила, з якою взаємодіють два точкових заряди і , визначається за формулою
, (2)
де r — відстань між зарядами; — відносна діелектрична проникність середовища; = 8,854∙10-12 Ф/м - електрична стала.
Якщо заряди однойменні, то сила, з якою заряд діє на заряд буде:
, (3)
де — радіус-вектор, проведений від заряду до заряду , - одиничний вектор.
Запишемо формулу (2) для нашого випадку взаємодії однакових зарядів:
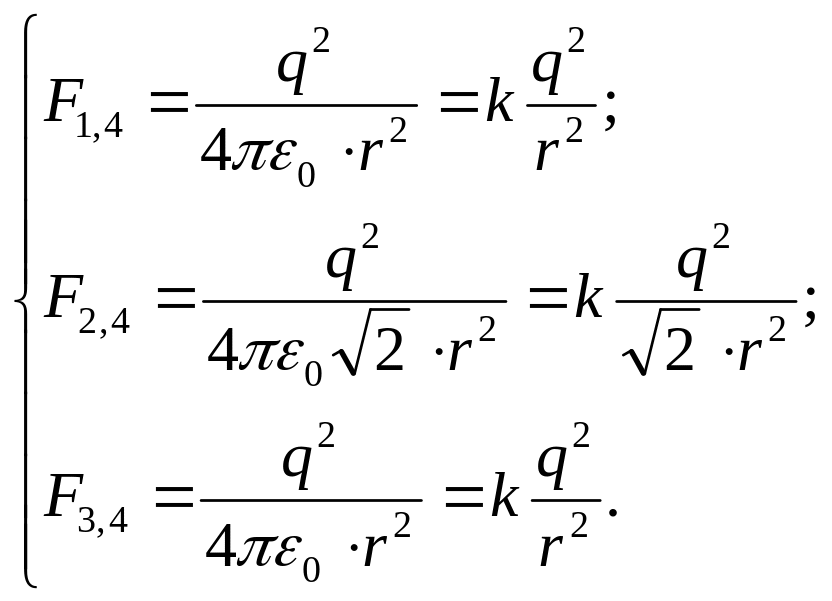 , (4)
, (4)
Силу
![]() ,
з якою діють перший і третій заряди на
четвертий, знаходимо з формулою теореми
косинусів
,
з якою діють перший і третій заряди на
четвертий, знаходимо з формулою теореми
косинусів
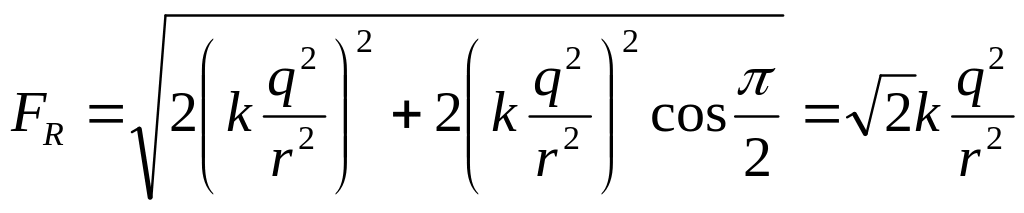 . (5)
. (5)
Тоді шукана сила дорівнює
![]() = (6)
= (6)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (6) і отримаємо відповідь:
=
3.20. Точкові заряди Q1 = 30 мкКл і Q2 = - 20 мкКл знаходяться на відстані d = 20 см один від одного. Визначити напруженість електричного поля Е в точці, що знаходиться на відстані r1 = 30 см від першого заряду, і на відстані r2 = 15 см від другого.
3.20.
Рис. 3.20
Дано
Q1
= 30 мкКл Q2
= - 20 мкКл
= 20 см
= 1
= 30 см
= 15 см
= ?
Відповідно до
принципу суперпозиції електричних
полів, кожний заряд створює поле незалежно
від присутності в просторі інших зарядів.
Тому напруженість
електричного поля в шуканій точці може
бути знайдена як геометрична сума
напруженості
і
полів, що утворюється кожним зарядом
окремо:
.
Напруженості електричного поля в точці
![]() ,
що утворюється в повітрі (
= 1) зарядами
і
,
,
що утворюється в повітрі (
= 1) зарядами
і
,
(1)
Вектор (рис. 3.15) спрямований по силовій лінії від заряду , тому що цей заряд позитивний; вектор спрямований також по силовій лінії, але до заряду , тому що цей заряд негативний.
Модуль вектора знайдемо за теоремою косинусів:
, (2)
де - кут між векторами і , косинус якого можемо знайти із трикутника зі сторонами і
![]() . (3)
. (3)
Підставляючи вираз і із (1), косинуса з (3) у (2) і виносячи спільний множник 1/(4л ) за знак кореня, одержуємо
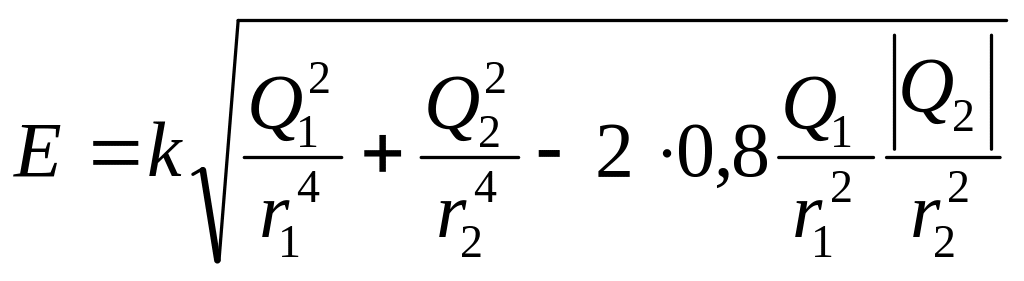 (4)
(4)
Зробимо підстановку заданих в умові задачі величин у формулу (4) і отримаємо відповіді:
=
3.21. У
вершинах правильного трикутника зі
стороною а
= 10 см знаходяться заряди
= 10 мкКл,
= 20 мкКл і
![]() = 30 мкКл. Визначити силу F, що діє на заряд
Q1
з боку двох інших зарядів.
= 30 мкКл. Визначити силу F, що діє на заряд
Q1
з боку двох інших зарядів.
3
Рис. 3.21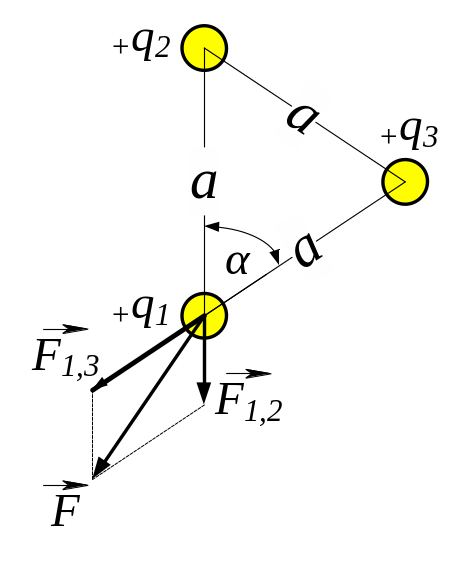
Дано
= 10 см
= 10 мкКл,
= 20 мкКл
= 30 мкКл
= ?
Відповідно до
принципу суперпозиції електричних
полів, кожний заряд створює поле незалежно
від присутності в просторі інших зарядів.
Тому напруженість
електричного поля в шуканій точці може
бути знайдена як геометрична сума
напруженості
![]() і
полів, що утворюється другим та третім
зарядами окремо:
і
полів, що утворюється другим та третім
зарядами окремо:![]() .
Напруженості електричного поля, що
утворюється в повітрі (
= 1) зарядами
і
,
.
Напруженості електричного поля, що
утворюється в повітрі (
= 1) зарядами
і
,
![]() (1)
(1)
Вектори
![]() і
і
![]() (рис. 3.21) спрямовані по силових лініях
від відповідних зарядів, тому що вони
позитивні.
(рис. 3.21) спрямовані по силових лініях
від відповідних зарядів, тому що вони
позитивні.
Модуль вектора знайдемо за теоремою косинусів:
![]() , (2)
, (2)
де
= 60о
- кут між векторами
![]() і
(трикутник
правильний).
і
(трикутник
правильний).
Шукану силу знаходимо за формулою:
![]() (3)
(3)
Зробимо підстановку заданих в умові задачі величин у формулу (3) і отримаємо відповідь:
=
3.22.
У вершинах квадрата знаходяться однакові
заряди
=
=
=
![]() =
= 8 10-10
Кл. Який негативний заряд
=
= 8 10-10
Кл. Який негативний заряд
![]() потрібно помістити в центрі квадрата,
щоб сила взаємного відштовхування
позитивних зарядів була урівноважена
силою притягання негативного заряду?
потрібно помістити в центрі квадрата,
щоб сила взаємного відштовхування
позитивних зарядів була урівноважена
силою притягання негативного заряду?
3.22.
Дано
q
= 8 10-10
Кл
= ?
За законом Кулона сила, з якою взаємодіють два точкових заряди і , визначається за формулою
Рис. 3.22
де r — відстань між зарядами; — відносна діелектрична проникність середовища; = 8,854∙10-12 Ф/м - електрична стала.
Якщо заряди однойменні, то сила, з якою заряд діє на заряд буде:
, (2)
де — радіус-вектор, проведений від заряду до заряду , - одиничний вектор.
Запишемо формулу (1) для всіх випадків взаємодії зарядів:
, (3)
Згідно рис. 3.5, сили і з системи (3) напрямлені під кутом 90о друг відносно другого, тому їхній додаток знаходимо за формулою:
. (4)
З рис. 3.5 видно, що повинна виконуватися рівність:
![]() . (5)
. (5)
Розв’язуємо рівняння (5) відносно шуканого заряду і отримаємо рівняння
q0 = (6)
Зробимо підстановку заданих в умові задачі величин у формулу (6) і отримаємо відповідь:
q0 =
3.23. На відстані = 20 см знаходяться два точкових заряди: = - 50 нКл і = 100 нКл. Визначити силу F, що діє на заряд = - 10 нКл, який знаходиться на однаковій відстані ( = 20 см) від обох зарядів.
3.23.
Дано
= 10 см
= - 50 нКл,
= 100 нКл
= - 10 нКл
= ?
За законом Кулона сила, з якою взаємодіють два точкових заряди і , визначається за формулою
Рис. 3.23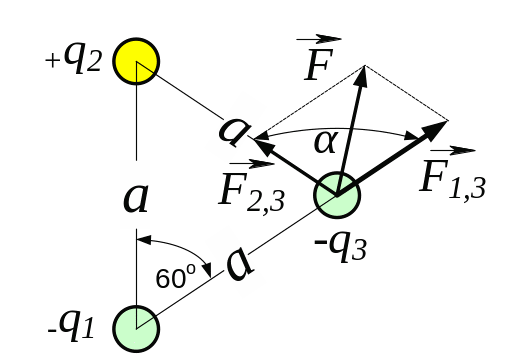
де r — відстань між зарядами; — відносна діелектрична проникність середовища; = 8,854∙10-12 Ф/м - електрична стала.
Якщо заряди однойменні, то сила, з якою заряд діє на заряд буде:
, (2)
де — радіус-вектор, проведений від заряду до заряду , - одиничний вектор.
Запишемо формулу (1) для взаємодії зарядів:
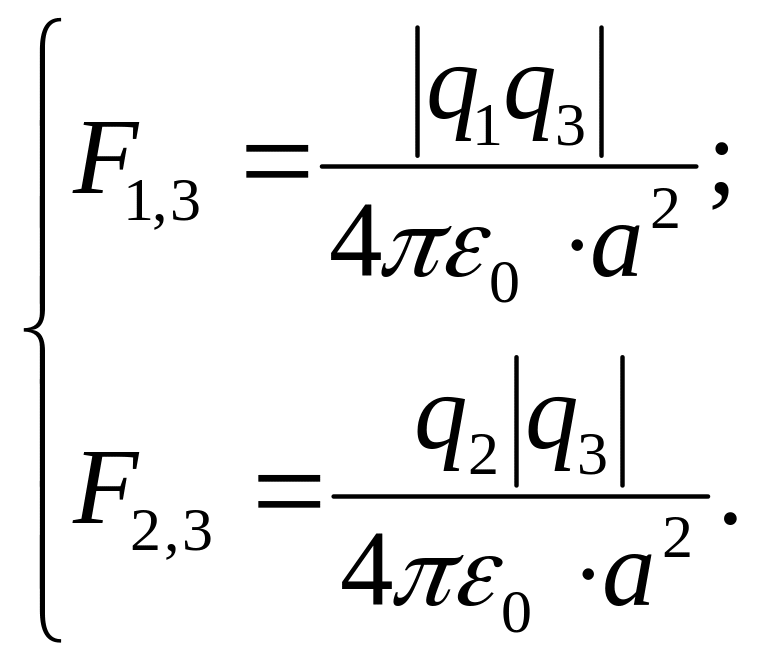 , (3)
, (3)
Згідно рис. 3.23,
сили
![]() і
і
![]() з системи (3) напрямлені під кутом 120о
друг відносно другого, тому їхній додаток
знаходимо за формулою:
з системи (3) напрямлені під кутом 120о
друг відносно другого, тому їхній додаток
знаходимо за формулою:
![]() . (4)
. (4)
Зробимо підстановку в формулу (4) сили з системи рівнянь (3) та заданих в умові задачі величин і отримаємо відповідь:
=
3.24. Відстань між двома точковими зарядами Q1 = 2 нКл і Q2 = 4 нКл дорівнює = 60 см. Визначити відстань, від першого заряду, на яку потрібно помістити третій заряд Q3 так, щоб система зарядів знаходилася в рівновазі.
3.24.
Дано
= 2 нКл
= 4 нКл
= 60 см
= ?
З
Рис. 3.24
, (1)
За законом Кулона сила, з якою взаємодіють два точкових заряди і , визначається за формулою
, (2)
де r — відстань між зарядами; — відносна діелектрична проникність середовища; = 8,854∙10-12 Ф/м - електрична стала.
Якщо заряди однойменні, то сила, з якою заряд діє на заряд буде:
, (3)
де — радіус-вектор, проведений від заряду до заряду , - одиничний вектор.
Запишемо формулу (2) для нашого випадку взаємодії точкових зарядів:
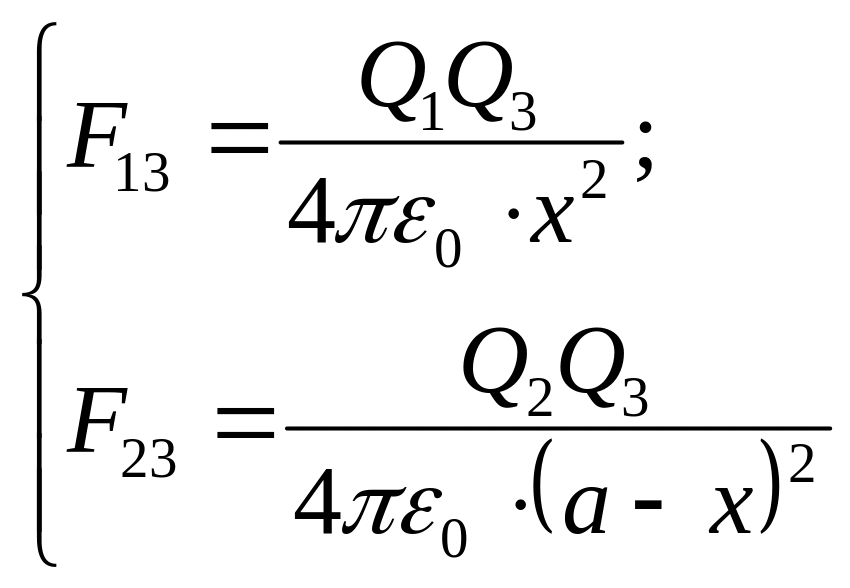 , (4)
, (4)
З виразу (1) отримуємо рівняння:
![]() , (5)
, (5)
Розв’язок рівняння (5) дає вираз для розрахунку відстані
=. (6)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (6) і отримаємо відповідь:
=
3.25. У
плоскому горизонтально розташованому
конденсаторі, відстань між пластинами
якого
= 1 см, знаходиться заряджена капелька
масою
= 5 10-11
г. При відсутності електричного поля
капелька внаслідок опору повітря падає
з деякою постійною швидкістю. Якщо до
конденсатора прикладена різниця
потенціалів
![]() = 600 В, то капелька падає вдвічі повільніше.
Знайти заряд капельки.
= 600 В, то капелька падає вдвічі повільніше.
Знайти заряд капельки.
3.24.
Рис. 3.25
Дано
= 1 см
= 5 10-11
г
= 600 В
= ?
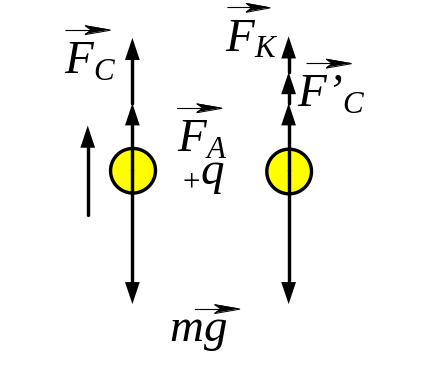
![]()
З рис. 3.25 випливає, що куля буде в рухатись з постійною швидкістю при умові виконання рівності сил, які діють на кулю в процесі її руху:
![]() , (1)
, (1)
де
![]() - сила Архімеда, якою ми нехтуємо;
- сила Архімеда, якою ми нехтуємо;
![]() - сила опору руху кулі, яку визначаємо
за формулою Стокса:
- сила опору руху кулі, яку визначаємо
за формулою Стокса:
![]() ,
бо
. (2)
,
бо
. (2)
За законом Кулона сила, з якою взаємодіють точковий заряд і електростатичне поле, визначається за формулою
![]() . (3)
. (3)
З виразу (1) отримуємо рівняння:
![]() , (4)
, (4)
Розв’язок рівнянь (3) і (4) дає вираз для розрахунку заряду капельки:
= (5)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (5) і отримаємо відповідь:
=
3
Рис. 3.26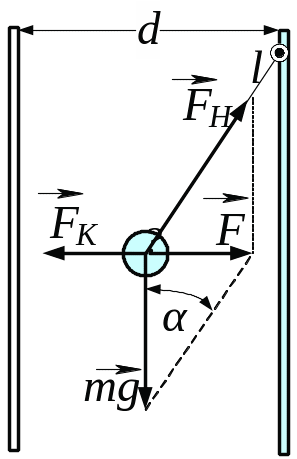
3.26.
Дано
= 1 см
= 0,1 г
= 1 кВ
= 10°
= ?
З рис. 3.26 випливає, що куля буде в рівновазі, якщо буде виконуватись рівність:
, (1)
За законом Кулона сила, з якою взаємодіє точковий заряди з зарядженою поверхнею, визначається за формулою
, (2)
де — напруженість електричного поля створеного зарядженими пластинами конденсатора (вважаємо їх нескінченими площинами), яку визначаємо за формулою
![]() . (3)
. (3)
Кут визначаємо з трикутника сил:
![]() , (4)
, (4)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (4) і отримаємо відповідь:
=
3.27. Мильний пузир з зарядом q = 222 пКл знаходиться в рівновазі в полі плоского горизонтально розташованого конденсатора. Знайти різницю потенціалів між пластинами конденсатора, якщо маса пузиря m = 0,01 г і відстань між пластинами = 5 см.
3.27.
Дано
q
= 222 пКл
m
= 0,01 г
= 5 см
= ?
Рис. 3.27
З рис. 3.27 видно, що куля буде в рівновазі, якщо буде виконуватись рівність модулів сил:
. (1)
За законом Кулона сила, з якою взаємодіє точковий заряди з електричним полем, визначається за формулою
, (2)
де — напруженість електричного поля в конденсаторі.
Тоді рівняння (1) записуємо у вигляді
![]() . (3)
. (3)
Значення різниці потенціалів визначаємо з рівняння (3):
= (4)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (4) і отримаємо відповідь:
=
3.28. Кулька радіусом R = 2 см заряджається негативно до потенціалу φ = 2 кВ. Знайти масу ієї кульки.
3.27.
Дано
R
= 2 см
φ
= 2 кВ
= ?
Масу усіх електронів, що складають заряд кульки, визначимо за формулою:
З рис. 3.27 видно, що куля буде в рівновазі, якщо буде виконуватись рівність модулів сил:
![]() , (1)
, (1)
де
![]() = 9,1∙10-31
кг – маса електрона;
= 9,1∙10-31
кг – маса електрона;
![]() = 1,6∙10-19
Кл – його заряд;
= 1,6∙10-19
Кл – його заряд;
![]() - кількість елементарних зарядів на
кульці, який визначаємо з ємності
відокремленого провідника, яка є
відношенням заряду до потенціалу
провідника:
- кількість елементарних зарядів на
кульці, який визначаємо з ємності
відокремленого провідника, яка є
відношенням заряду до потенціалу
провідника:
![]() , (2)
, (2)
де ємність провідної кулі радіуса дорівнює
![]() . (3)
. (3)
Загальний заряд усіх електронів на кулі знаходимо з рівняння (3) і підставляємо у вираз (1):
= (4)
Зробимо підстановку заданих в умові задачі величин (виражених у системі СІ) у формулу (4) і отримаємо відповідь:
=
3.29. Вісім заряджених водяних крапель радіусом = 1 мм і зарядом q = 1 нКл кожна, зливаються в одну загальну водяну краплю. Знайти потенціал φ цієї новоутвореної краплі.
3.29.
Дано
= 1 мм q
= 1 нКл
![]() = 8
= 8
![]() = ?
= ?
Під час злиття краплин в одну сталими залишаються їхні загальні заряд та об’єм:
![]() (1)
(1)
де
- заряд великої краплі;
,
![]() ,
- заряд, ємність і радіус малої краплі;
,
- заряд, ємність і радіус малої краплі;
![]() - радіус великої краплі.
- радіус великої краплі.
Потенціал великої краплі знаходимо за формулою
![]() . (2)
. (2)
Зробимо підстановку заданих в умові задачі величин у формулу (2):
=
3.30. Дві кульки радіусом = 1 см і масою = 40 мг підвішені на нитках довжиною 10 см так, що їх поверхні стикаються. Коли кульки зарядили, нитки розійшлися на деякий кут і сила натягнення ниток стала рівною = 490 мкН. Знайти потенціал φ заряджених кульок.
Рис. 3.30
3.30.
Дано
= 1 см
= 40 мг
= 10 см
= 490 мкН
= ?
Потенціал кульки знаходимо за формулою
![]() . (1)
. (1)
Заряд кульок визначаємо з їхньої взаємодії.
За законом Кулона сила, з якою взаємодіють два точкових заряди і , визначається за формулою
, (2)
де r — відстань між зарядами; — відносна діелектрична проникність середовища; = 8,854∙10-12 Ф/м - електрична стала.
Якщо заряди однойменні, то сила, з якою заряд діє на заряд буде:
, (3)
де — радіус-вектор, проведений від заряду до заряду , - одиничний вектор.
Запишемо формулу (1) для нашого випадку взаємодії однакових зарядів:
, (4)
де
![]() ,
а
,
а
![]() визначаємо з подібності трикутників.
визначаємо з подібності трикутників.
Згідно рис. 3.30, сили і зрівноважують одна одну тому заряди знаходяться в рівновазі. Останню силу визначаємо з прямокутного трикутника і отримуємо рівняння:
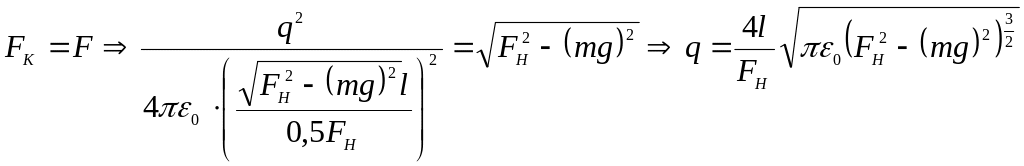 , (5)
, (5)
Заряд кулі з формули (5) підставляємо у формулу (1) і отримаємо вираз для розрахунку відповіді:
= (6)
Зробимо підстановку заданих в умові задачі величин у формулу (5) і отримаємо відповідь:
=
3.31. На деякій відстані від нескінченної рівномірно зарядженої площини з поверхневою густиною заряду σ = 2 мкКл/м2 розміщений круг радіусом = 15 см, який паралельний площині. Знайти потік вектора напруженості електричного поля крізь цей круг.
3
Дано
σ = 2 мкКл/м2
= 15 см
![]() = ?
= ?
Розв’язок.
Потік вектора
через усю поверхню, площа якої
![]() виразиться сумою елементарних потоків,
або інтегралом
виразиться сумою елементарних потоків,
або інтегралом
![]() , (1)
, (1)
де - кут між нормаллю до поверхні і вектором напруженості поля.
Напруженість електростатичного поля рівномірно зарядженої нескінченної площини визначається за формулою:
![]() =
=
![]() . (2)
. (2)
Тоді формула (1) матиме вигляд
![]() , (3)
, (3)
Зробимо підстановку заданих в умові задачі величин у формулу (3) і отримаємо відповідь:
=
3.32.
Заряд q
= 1 мкКл знаходиться в вершині кругового
конуса висота якого
![]() = 30 см, радіус основи
= 10 см. Знайти потік вектора напруженості
електричного поля крізь поверхню цього
конуса.
= 30 см, радіус основи
= 10 см. Знайти потік вектора напруженості
електричного поля крізь поверхню цього
конуса.
3
Дано
q
= 1 мкКл
= 30 см
= 10 см
= ?
Рис. 3.32
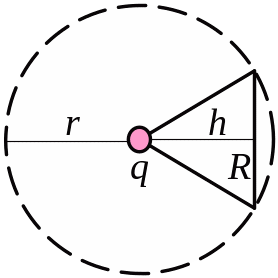
Розв’язок.
Навколо заряду, з центром де він знаходиться, проводимо сферичну поверхню радіусом , який дорівнює твірній бокової поверхні конуса. З рис. 3.32 видно, що потік вектора напруженості поля крізь поверхню конуса дорівнює потоку, який пронизує тільки його основу. Тобто потоку крізь сферичний сегмент радіусом , площа якого дорівнює
![]() . (1)
. (1)
Площа сферичної поверхні дорівнює
![]() . (2)
. (2)
Повний потік вектора напруженості крізь сферичну поверхню дорівнює
![]() , (3)
, (3)
Тоді шуканий потік знаходимо за формулою
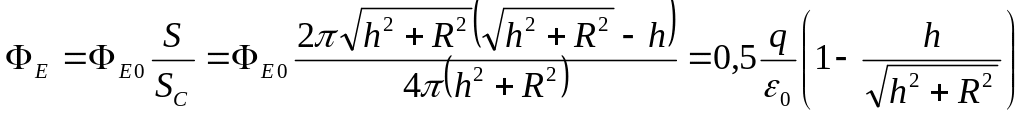 , (4)
, (4)
Зробимо підстановку заданих в умові задачі величин у формулу (4) і отримаємо відповідь:
=
3.33. На
осі конуса, що знаходиться у вакуумі,
на однакових відстанях від вершини і
центра основи розміщений точковий заряд
q
= 1 мкКл. Висота конуса
![]() = 20 см, а радіус основи
= 10 см. Знайти потік вектора напруженості
електричного поля крізь поверхню основи
конуса.
= 20 см, а радіус основи
= 10 см. Знайти потік вектора напруженості
електричного поля крізь поверхню основи
конуса.
3
Дано
q
= 1 мкКл
= 20 см
= 10 см
= ?
Рис. 3.33
Розв’язок.
Навколо заряду, з
центром де він знаходиться, проводимо
сферичну поверхню радіусом
![]() (див. рис.3.33).
(див. рис.3.33).
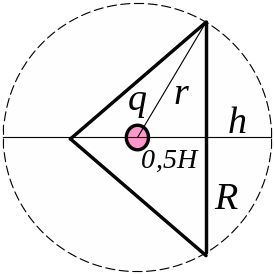
З рис. 3.33 видно, що потік вектора напруженості поля крізь поверхню основи конуса дорівнює потоку, який пронизує сферичний сегмент висотою , площа якого дорівнює
![]() .
(1)
.
(1)
Площа сферичної поверхні дорівнює
![]() . (2)
. (2)
Повний потік вектора напруженості крізь сферичну поверхню дорівнює (згідно з теоремою Гауса)
, (3)
Тоді шуканий потік знаходимо за формулою
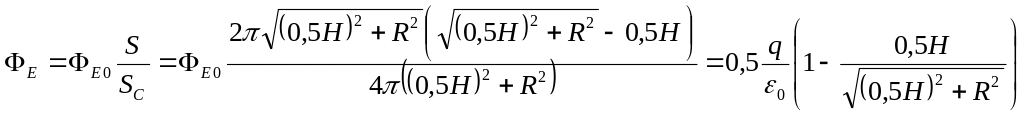 ,
(4)
,
(4)
Зробимо підстановку заданих в умові задачі величин у формулу (4) і отримаємо відповідь:
=
3.34. На осі конуса, що знаходиться у вакуумі, на однакових відстанях від вершини і центра основи розміщений точковий заряд q = 1 мкКл. Висота конуса = 20 см, а радіус основи = 10 см. Знайти потік вектора напруженості електричного поля крізь бокову поверхню конуса.
3
Дано
q
= 1 мкКл
= 20 см
= 10 см
= ?
Рис. 3.34
Розв’язок.
Навколо заряду, з центром де він знаходиться, проводимо сферичну поверхню радіусом (див. рис.3.34).
З рис. 3.34 видно, що потік вектора напруженості поля крізь бокову поверхню конуса дорівнює потоку, який не пронизує сферичний сегмент висотою , площа якого дорівнює
. (1)
Площа сферичної поверхні дорівнює
. (2)
Повний потік вектора напруженості крізь сферичну поверхню дорівнює (згідно з теоремою Гауса)
, (3)
Тоді шуканий потік знаходимо за формулою
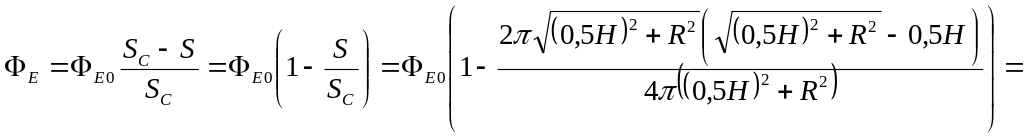
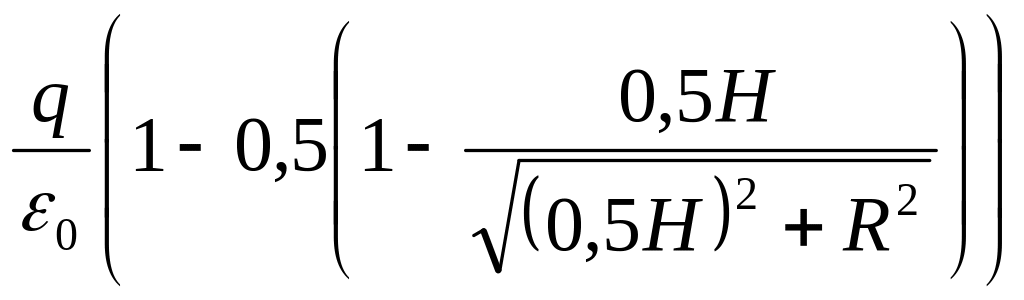 ,
(4)
,
(4)
Зробимо підстановку заданих в умові задачі величин у формулу (4) і отримаємо відповідь:
=
3
Рис. 3.35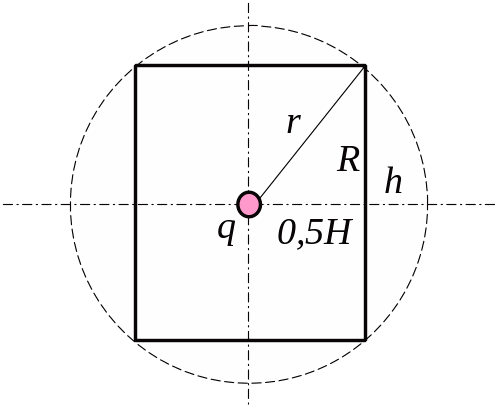
3.35.
Дано
q
= 0,3 мкКл
= 20 см
= 10 см
= ?
Навколо заряду, з центром де він знаходиться, проводимо сферичну поверхню радіусом (див. рис.3.35).
З рис. 3.35 видно, що потік вектора напруженості поля крізь бокову поверхню циліндра дорівнює потоку, який не пронизує поверхні його основ, тобто поверхні двох сферичних сегментів висотою , площа яких дорівнює
![]() .
(1)
.
(1)
Площа сферичної поверхні дорівнює
. (2)
Повний потік вектора напруженості крізь сферичну поверхню дорівнює (згідно з теоремою Гауса)
, (3)
Тоді шуканий потік знаходимо за формулою
 ,
(4)
,
(4)
Зробимо підстановку заданих в умові задачі величин у формулу (4) і отримаємо відповідь:
=
3.36. Знайти потік вектора напруженості електричного поля крізь бокову поверхню прямого кругового циліндра висотою = 20 см, з основою радіусом = 10 см. Точковий заряд q = 0,3 мкКл розміщений у центрі основи циліндра.
3.36.
Дано
q
= 0,3 мкКл
= 20 см
= 10 см
= ?
Рис. 3.36
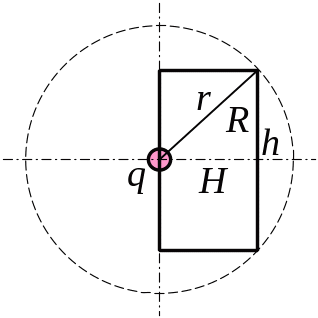
Навколо заряду, з
центром де він знаходиться, проводимо
сферичну поверхню радіусом
![]() (див. рис.3.36).
(див. рис.3.36).
З рис. 3.36 видно, що потік вектора напруженості поля крізь бокову поверхню циліндра дорівнює потоку, який не пронизує ліву половину сферичної поверхні та поверхню його основи, тобто поверхню сферичного сегменту висотою , площа якої дорівнює
![]() .
(1)
.
(1)
Площа сферичної поверхні дорівнює
![]() . (2)
. (2)
Повний потік вектора напруженості крізь сферичну поверхню дорівнює (згідно з теоремою Гауса)
, (3)
Тоді шуканий потік знаходимо за формулою
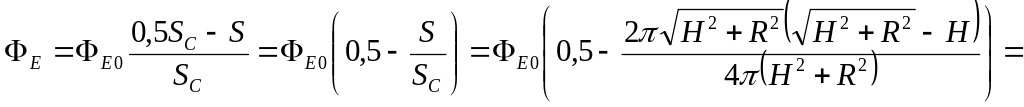
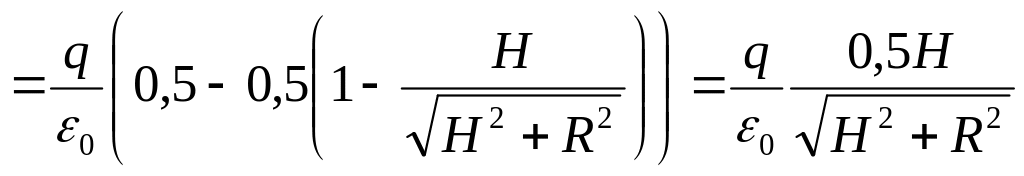 ,
(4)
,
(4)
Зробимо підстановку заданих в умові задачі величин у формулу (4) і отримаємо відповідь:
=
3.37. Кільце з дроту радіусом 10 см має негативний заряд q' = - 5 нКл. Знайти напруженість електричного поля на осі кільця в точках, розташованих від центра кільця на відстанях, рівних 0 і 15 см. На якій відстані від центра кільця напруженість електричного поля буде мати максимальне значення?
3.37.
Дано
q
= - 5 нКл
= 10 см
![]() = 0
= 0![]() = 15 см
= 15 см
![]() = ?
= ?
![]() = ?
= ?![]() = ?
= ?
З'єднаємо координатну
площину хОу
з площиною кільця, а вісь Оz
- із віссю кільця (рис. 3.36). На кільці
виділимо малу ділянку довжиною
![]() .
Оскільки заряд
.
Оскільки заряд
![]() ,
що знаходиться на цій ділянці, можна
вважати точковим, то напруженість
,
що знаходиться на цій ділянці, можна
вважати точковим, то напруженість
![]() електричного поля, що утворюється цим
зарядом, може бути записана у вигляді
електричного поля, що утворюється цим
зарядом, може бути записана у вигляді
![]() (1)
(1)
де
![]() - радіус-вектор, направлений від елемента
до точки А;
- радіус-вектор, направлений від елемента
до точки А;
![]() - лінійна густина заряду на кільці.
- лінійна густина заряду на кільці.
Розкладемо вектор
(для спрощення малювання рис. 3.37, заряд
вважаємо додатнім) на дві складові:
![]() перпендикулярно площині кільця (спів
напрямлену з віссю Oz),
і
перпендикулярно площині кільця (спів
напрямлену з віссю Oz),
і
![]() ,
паралельну площині кільця (площини
хОу),
тобто
,
паралельну площині кільця (площини
хОу),
тобто
![]() (2)
(2)
Напруженість електричного поля в точці А знайдемо інтегруванням:
Рис. 3.37![]()
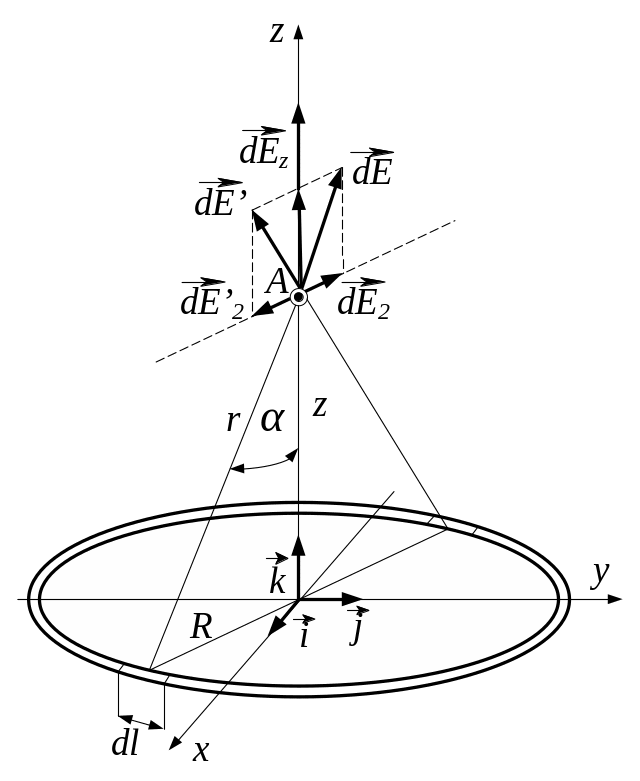
де інтегрування
ведемо по всіх елементах зарядженого
кільця. Зауважимо, що для кожної пари
зарядів
![]() і
і
![]()
![]() розташованих симетрично щодо центру
кільця, вектори
і
розташованих симетрично щодо центру
кільця, вектори
і
![]() у точці А
рівні за модулем і протилежні за напрямом:
у точці А
рівні за модулем і протилежні за напрямом:
![]()
Тому векторна сума
(інтеграл)
![]() = 0 Складові
для всіх елементів кільця спів напрямлені
з віссю Oz
(одиничним вектором
= 0 Складові
для всіх елементів кільця спів напрямлені
з віссю Oz
(одиничним вектором
![]() ),
тобто
),
тобто
![]() Тоді
Тоді
![]()
Тому що
![]() а
а
![]() і
і
![]() то
то
![]() (4)
(4)
Отже,
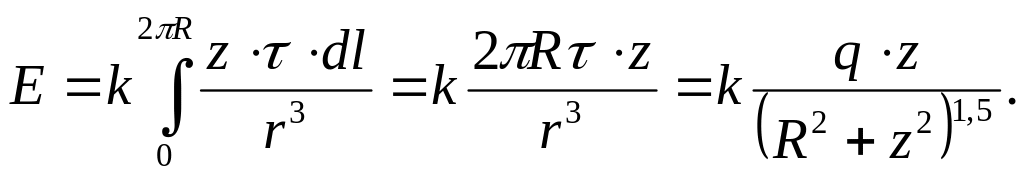 (5)
(5)
для = 0 напруженість електричного поля теж буде дорівнювати нулю:
для
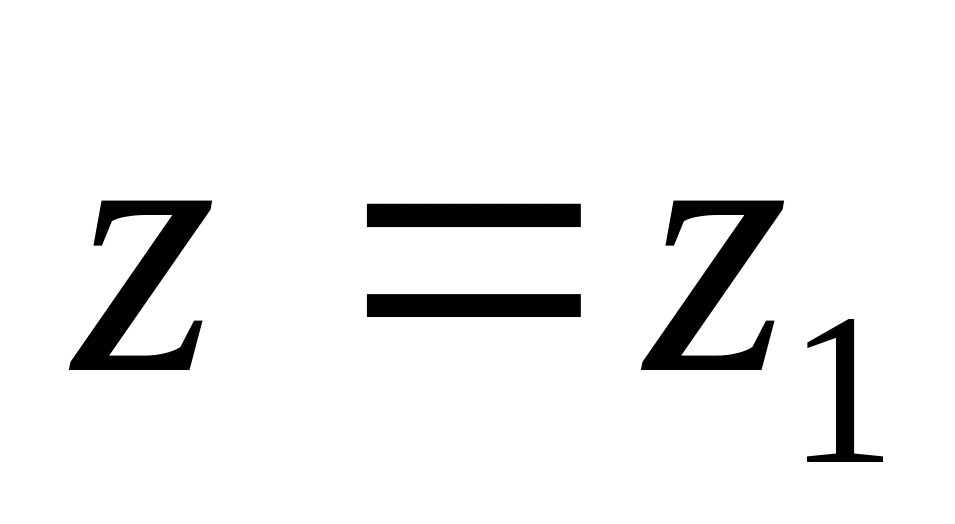 розрахунок напруженості поля виконуємо
за формулою (5) і отримаємо відповідь:
розрахунок напруженості поля виконуємо
за формулою (5) і отримаємо відповідь:
=
максимальне значення напруженості поля, яке створюється зарядженим кільцем у точках на вісі
 ,
визначаємо із
співвідношення:
,
визначаємо із
співвідношення:
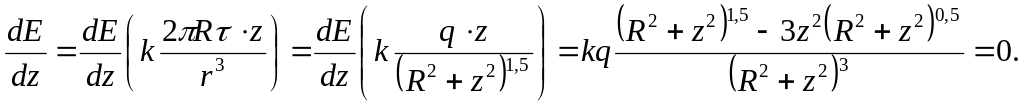 (6)
(6)
Оскільки знаменник не дорівнює нулю, то отримуємо
![]() . (7)
. (7)
Тоді відстань від центра кільця до точки, на його вісі симетрії (по обидві сторони від кільця), де напруженість поля набуває максимального значення розрахуємо за формулою (7):
![]() =
=
3.38. Напруженість електричного поля на осі зарядженого кільця має максимальне значення на відстані L від центра кільця. У скільки разів напруженість електричного поля в точці, розташованій на відстані 0,5 L від центра кільця, буде менше максимального значення напруженості?
3.38.
Дано
= 0,5 L
![]() = L
= L
![]() = ?
= ?
Зробимо малюнок.
З
Рис. 3.38
(1)
де - радіус-вектор, направлений від елемента до точки А; - лінійна густина заряду на кільці.
Розкладемо вектор (для спрощення малювання рис. 3.37, заряд вважаємо додатнім) на дві складові: перпендикулярно площині кільця (спів напрямлену з віссю Oz), і , паралельну площині кільця (площини хОу), тобто
(2)
Напруженість електричного поля в точці А знайдемо інтегруванням:
(3)
де інтегрування ведемо по всіх елементах зарядженого кільця. Зауважимо, що для кожної пари зарядів і розташованих симетрично щодо центру кільця, вектори і у точці А рівні за модулем і протилежні за напрямом:
Тому векторна сума (інтеграл) = 0 Складові для всіх елементів кільця спів напрямлені з віссю Oz (одиничним вектором ), тобто Тоді
Тому що
а і то (4)
Отже,
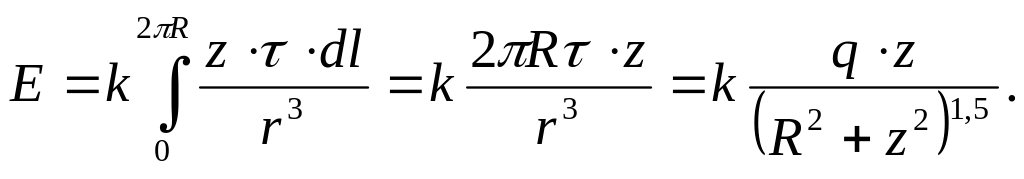 (5)
(5)
Максимальне значення напруженості поля, яке створюється зарядженим кільцем у точках на вісі , визначаємо із співвідношення:
(6)
Оскільки знаменник не дорівнює нулю, то отримуємо
![]() . (7)
. (7)
З рівняння (7) визначаємо радіус кільця
![]() . (8)
. (8)
Шукане відношення визначаємо за допомогою формули (5)
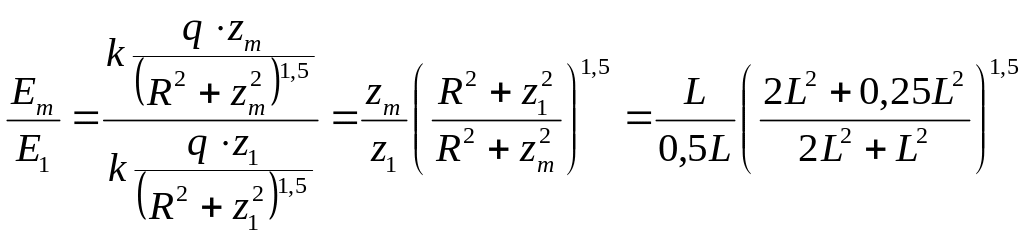 . (9)
. (9)
Спрощуємо рівняння (9) і визначаємо в скільки разів напруженість електричного поля в точці, розташованій на відстані 0,5 L від центра кільця, буде менше максимального значення напруженості:
=
3.39. Тонкий довгий стержень рівномірно заряджений з лінійною густиною τ = 1,5 нКл/см. На продовженні осі стержня на відстані = 12 см від його кінця знаходиться точковий заряд Q = 0,2 мкКл. Визначити силу взаємодії зарядженого стержня і точкового заряду.
3.39.
Рис. 3.39
Дано
τ
= 1,5 нКл/см
= 12 см Q
= 0,2 мкКл
= ?
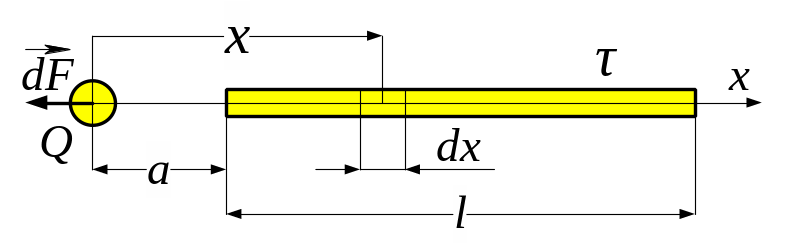
Сила взаємодії зарядженого стержня з точковим зарядом залежить від лінійної густини заряду на стрижні.
При обчисленні
сили
варто мати на увазі, що заряд на стрижні
не є точковим, тому закон Кулона
безпосередньо застосувати не можна. У
цьому випадку можна зробити так. Виділимо
на стрижні (рис. 3.39) малу ділянку
![]() із зарядом
із зарядом
![]() .
Цей заряд можна розглядати як точковий.
Тоді, відповідно до закону Кулона, сила
взаємодії точкових зарядів дорівнює:
.
Цей заряд можна розглядати як точковий.
Тоді, відповідно до закону Кулона, сила
взаємодії точкових зарядів дорівнює:
![]() (1)
(1)
Інтегруючи цей вираз у межах від до нескінченності, маємо
![]() . (2)
. (2)
Підставляємо величини, які задані в умові задачі (виражені в одиницях системи СІ), у вираз (2) і отримуємо:
=
Перевіримо, чи дає розрахункова формула одиницю сили. Для цього в праву частину формули замість символів розмірів підставимо їхні одиниці:
![]() .
.
3.40. Тонкий стержень довжиною = 20 см несе рівномірно розподілений заряд q = 0,1 мкКл. Визначити напруженість електростатичного поля у точці, що лежить, по осі стержня, на відстані = 20 см від його кінця.
3.40.
Дано
= 20 см q
= 0,1 мкКл
= 12 см Q
= 0,2 мкКл
= ?
Рис. 3.40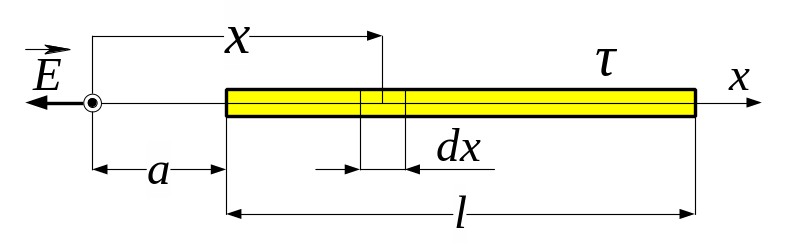
![]() (1)
(1)
безпосередньо застосувати не можна. У цьому випадку зробимо так. Виділимо на стрижні (рис. 3.40) малу ділянку із зарядом ( лінійна густина заряду на стержні). Цей заряд можна розглядати як точковий. Тоді формулу (1), для цього точкового заряду запишемо так
![]() (2)
(2)
Інтегруючи цей
вираз у межах від
до
![]() ,
маємо
,
маємо
![]() . (3)
. (3)
Підставляємо величини, які задані в умові задачі (виражені в одиницях системи СІ), у вираз (3) і отримуємо:
=
Перевіримо, чи дає розрахункова формула одиницю напруженості. Для цього в праву частину формули замість символів розмірів підставимо їхні одиниці:
![]() .
.
3.41. По тонкому півкільцю радіуса = 10 см рівномірно розподілений заряд з лінійною густиною τ = 1 мкКл/м. Визначити напруженість електричного поля в точці, що збігається з центром кільця.
3
Рис. 3.41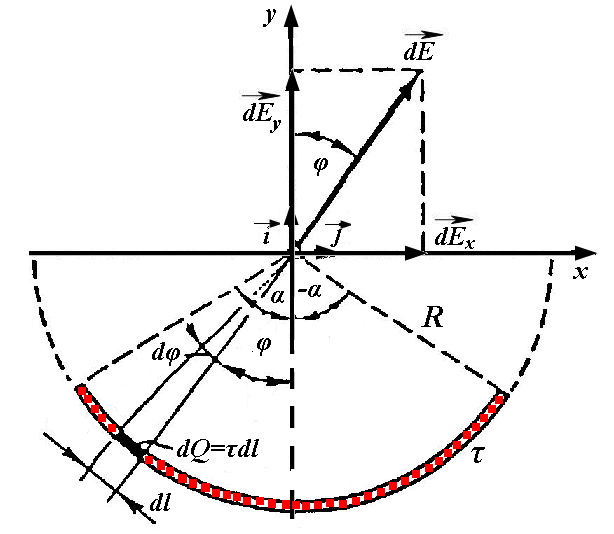
О
Дано
= 10 см τ
= 1 мкКл/м
= 90о
= ?
Визначимо
напруженість електричного поля в точці
де перетинаються вісі координат. Для
цього знайдемо спочатку напруженість
![]() поля, що створюється зарядом
:
поля, що створюється зарядом
:
![]() (1)
(1)
де - радіус-вектор, спрямований від елемента до точки, у якій обчислюється напруженість.
Виразимо вектор
через проекції
і
![]() на
осі координат:
на
осі координат:
![]() де
де
![]() та
та
![]() - одиничні вектори напрямків (орти).
Напруженість
знайдемо інтегруванням:
- одиничні вектори напрямків (орти).
Напруженість
знайдемо інтегруванням:
![]() (2)
(2)
Інтегрування
ведемо уздовж дуги довжиною
.
У силу симетрії
![]() .
Тоді
.
Тоді
![]() , (3)
, (3)
де
![]() Оскільки
Оскільки
![]()
![]() ,
то
,
то
![]() (4)
(4)
Підставимо вираз
![]() у (3) і, взявши до уваги симетричне
розташування дуги щодо осі Оу,
межі інтегрування оберемо від 0 до
у (3) і, взявши до уваги симетричне
розташування дуги щодо осі Оу,
межі інтегрування оберемо від 0 до
![]() /2,
а результат подвоїмо:
/2,
а результат подвоїмо:
![]() (5)
(5)
З цієї формули видно, що напруженість поля за напрямком збігається з віссю Оу. Підставляємо величини, які задані в умові задачі (виражені в одиницях системи СІ), у вираз (5) і отримуємо:
=
3.42. Тонке кільце несе розподілений заряд = 0,2 мкКл. Визначити напруженість електричного поля в точці, що рівновіддалена від усіх точок кільця на відстань = 20 см. Радіус кільця R = 10 см.
3.42.
Дано
= 0,2 мкКл
= 20 см R
= 10 см
= ?
З
Рис. 3.42
З'єднаємо координатну площину хОу з площиною кільця, а вісь Оz - із віссю кільця (рис. 3.42). На кільці виділимо малу ділянку довжиною . Оскільки заряд , що знаходиться на цій ділянці, можна вважати точковим, то напруженість електричного поля, що утворюється цим зарядом, може бути записана у вигляді
(1)
де - радіус-вектор, направлений від елемента до точки А; - лінійна густина заряду на кільці.
Розкладемо вектор (для спрощення малювання рис. 3.42, заряд вважаємо додатнім) на дві складові: перпендикулярно площині кільця (спів напрямлену з віссю Oz), і , паралельну площині кільця (площини хОу), тобто
(2)
Напруженість електричного поля в точці А знайдемо інтегруванням:
(3)
де інтегрування ведемо по всіх елементах зарядженого кільця. Зауважимо, що для кожної пари зарядів і розташованих симетрично щодо центру кільця, вектори і у точці А рівні за модулем і протилежні за напрямом:
Тому векторна сума (інтеграл) = 0 Складові для всіх елементів кільця спів напрямлені з віссю Oz (одиничним вектором ), тобто Тоді
Тому що
а то (4)
Отже,
![]() . (5)
. (5)
Підставляємо величини, які задані в умові задачі (виражені в одиницях системи СІ), у вираз (5) і отримуємо:
=
3.43. Третина тонкого кільця радіуса R = 10 см несе розподілений заряд Q = 50 нКл. Визначити напруженість електричного поля в точці О, що збігається з центром цього кільця.
3
Рис. 3.41
О
Дано
= 10 см Q
= 50 нКл
= 60о
= ?
Визначимо напруженість електричного поля в точці де перетинаються вісі координат. Для цього знайдемо спочатку напруженість поля, що створюється зарядом :
(1)
де - радіус-вектор, спрямований від елемента до точки, у якій обчислюється напруженість.
Виразимо вектор через проекції і на осі координат: де та - одиничні вектори напрямків (орти). Напруженість знайдемо інтегруванням:
(2)
Інтегрування ведемо уздовж дуги довжиною . У силу симетрії . Тоді
, (3)
де Оскільки , то
(4)
Підставимо вираз у (3) і, взявши до уваги симетричне розташування дуги щодо осі Оу, межі інтегрування оберемо від 0 до /2, а результат подвоїмо:
![]() (5)
(5)
З цієї формули видно, що напруженість поля за напрямком збігається з віссю Оу. Підставляємо величини, які задані в умові задачі (виражені в одиницях системи СІ), у вираз (5) і отримуємо:
=
3.44. Нескінченний тонкий стержень, обмежений з одного боку, несе рівномірно розподілений заряд з лінійною густиною τ = 0,5 мкКл/м. Визначити напруженість електричного поля в точці, що знаходиться по осі стержня на відстані = 20 см від його початку.
3.44. Розв'язок.
П
Дано
τ = 0,5 мкКл/м
= 20 см
= ?
Рис. 3.40
безпосередньо застосувати не можна. У цьому випадку зробимо так. Виділимо на стрижні (рис. 3.40) малу ділянку із зарядом ( лінійна густина заряду на стержні). Цей заряд можна розглядати як точковий. Тоді формулу (1), для цього точкового заряду запишемо так
(2)
Інтегруючи цей
вираз у межах від
до
![]() ,
маємо
,
маємо
![]() . (3)
. (3)
Підставляємо величини, які задані в умові задачі (виражені в одиницях системи СІ), у вираз (3) і отримуємо:
=
Перевіримо, чи дає розрахункова формула одиницю напруженості. Для цього в праву частину формули замість символів розмірів підставимо їхні одиниці:
.
3.45. По
тонкому кільцю радіусом R
= 20 см розмірно розподілений заряд з
лінійною густиною τ
= 0,2 мкКл/м. Визначити напруженість
електричного поля в точці, що знаходиться
на осі кільця на відстані
![]() = 2R
від його центра.
= 2R
від його центра.
3.45.
Дано
τ
= 0,2 мкКл/м R
= 20 см
= ?
![]() см
см
Зробимо малюнок.
З'єднаємо координатну площину хОу з площиною кільця, а вісь Оz - із віссю кільця (рис. 3.45). На кільці виділимо малу ділянку довжиною . Оскільки заряд , що знаходиться на цій ділянці, можна вважати точковим, то напруженість електричного поля, що утворюється цим зарядом, може бути записана у вигляді
(1)
д
Рис. 3.45
Розкладемо вектор (для спрощення малювання рис. 3.45, заряд вважаємо додатнім) на дві складові: перпендикулярно площині кільця (спів напрямлену з віссю Oz), і , паралельну площині кільця (площини хОу), тобто
(2)
Напруженість електричного поля в точці А знайдемо інтегруванням:
(3)
де інтегрування ведемо по всіх елементах зарядженого кільця. Зауважимо, що для кожної пари зарядів і розташованих симетрично щодо центру кільця, вектори і у точці А рівні за модулем і протилежні за напрямом:
Тому векторна сума (інтеграл) = 0 Складові для всіх елементів кільця спів напрямлені з віссю Oz (одиничним вектором ), тобто Тоді
Тому що
а то (4)
Отже,
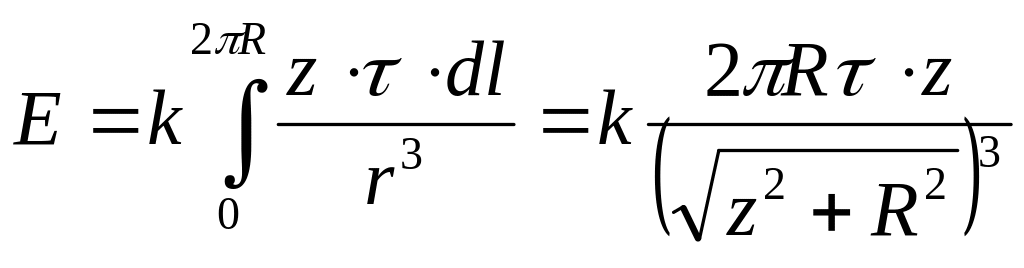 . (5)
. (5)
Підставляємо величини, які задані в умові задачі (виражені в одиницях системи СІ), у вираз (5) і отримуємо:
=
3.46. По тонкому півкільцю рівномірно розподілений заряд Q = 20 мкКл із лінійною густиною τ = 0,1 мкКл/м. Визначити напруженість електричного поля в точці О, що збігається з центром цього кільця.
3
Рис. 3.46
О
Дано
= 10 см τ
= 1 мкКл/м
= 90о
= ?
Визначимо напруженість електричного поля в точці де перетинаються вісі координат. Для цього знайдемо спочатку напруженість поля, що створюється зарядом :
(1)
де - радіус-вектор, спрямований від елемента до точки, у якій обчислюється напруженість.
Виразимо вектор через проекції і на осі координат: де та - одиничні вектори напрямків (орти). Напруженість знайдемо інтегруванням:
(2)
Інтегрування ведемо уздовж дуги довжиною . У силу симетрії . Тоді
, (3)
де Оскільки , то
(4)
Підставимо вираз у (3) і, взявши до уваги симетричне розташування дуги щодо осі Оу, межі інтегрування оберемо від 0 до /2, а результат подвоїмо:
![]() (5)
(5)
Радіус кола визначаємо з виразу лінійної густини:
![]() , (6)
, (6)
Радіус з цієї формули підставляємо в вираз (5), в отриманий вираз підставляємо величини, які задані в умові задачі (виражені в одиницях системи СІ):
=
3.47. Чверть тонкого кільця радіусом 10 см несе рівномірно розподілений заряд Q = 0,05 мкКл. Визначити напруженість електричного поля в точці, що збігається з центром цього кільця.
3
Рис. 3.47
О
Дано
= 10 см Q
= 0,05 мкКл
= 45о
= ?
![]() лінійна густина заряду на
четверті тонкого кільця),
що знаходиться на виділеній ділянці,
можна вважати точковим.
лінійна густина заряду на
четверті тонкого кільця),
що знаходиться на виділеній ділянці,
можна вважати точковим.
Визначимо напруженість електричного поля в точці де перетинаються вісі координат. Для цього знайдемо спочатку напруженість поля, що створюється зарядом :
(1)
де - радіус-вектор, спрямований від елемента до точки, у якій обчислюється напруженість.
Виразимо вектор через проекції і на осі координат: де та - одиничні вектори напрямків (орти). Напруженість знайдемо інтегруванням:
(2)
Інтегрування ведемо уздовж дуги довжиною . У силу симетрії . Тоді
, (3)
де Оскільки , то
(4)
Підставимо вираз у (3) і, взявши до уваги симетричне розташування дуги щодо осі Оу, межі інтегрування оберемо від 0 до /4, а результат подвоїмо:
![]() (5)
(5)
З цієї формули видно, що напруженість поля за напрямком збігається з віссю Оу. Підставляємо величини, які задані в умові задачі (виражені в одиницях системи СІ), у вираз (5) і отримуємо:
=
3
Рис. 3.48
3.48.
Дано
Q
= 10 нКл τ
= 0,01 мкКл/м
= ?
![]() см
см
Зробимо малюнок.
З'єднаємо координатну площину хОу з площиною кільця, а вісь Оz - із віссю кільця (рис. 3.48). На кільці виділимо малу ділянку довжиною . Оскільки заряд , що знаходиться на цій ділянці, можна вважати точковим, то напруженість електричного поля, що утворюється цим зарядом, може бути записана у вигляді
(1)
де - радіус-вектор, направлений від елемента до точки А.
Розкладемо вектор (для спрощення малювання рис. 3.48, заряд вважаємо додатнім) на дві складові: перпендикулярно площині кільця (спів напрямлену з віссю Oz), і , паралельну площині кільця (площини хОу), тобто
(2)
Напруженість електричного поля в точці А знайдемо інтегруванням:
(3)
де інтегрування ведемо по всіх елементах зарядженого кільця. Зауважимо, що для кожної пари зарядів і розташованих симетрично щодо центру кільця, вектори і у точці А рівні за модулем і протилежні за напрямом:
Тому векторна сума (інтеграл) = 0 Складові для всіх елементів кільця спів напрямлені з віссю Oz (одиничним вектором ), тобто Тоді
Тому що
а то (4)
Отже,
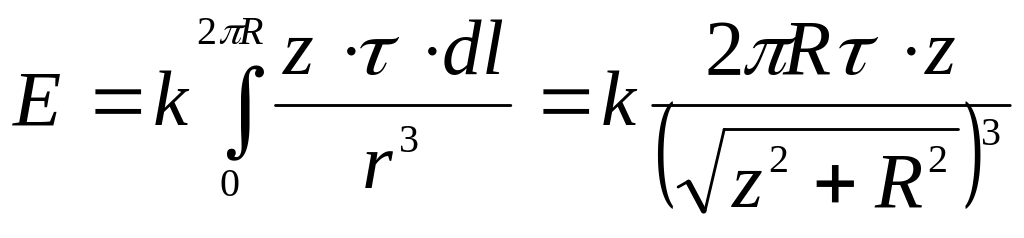 . (5)
. (5)
Радіус кола визначаємо з виразу лінійної густини:
![]() , (6)
, (6)
Радіус з цієї формули підставляємо в вираз (5), в отриманий вираз підставляємо величини, які задані в умові задачі (виражені в одиницях системи СІ):
=
3.49. Дві третини тонкого кільця радіусом R = 10 см несуть рівномірно розподілений з лінійною густиною τ = 0,2 мкКл/м заряд. Визначити напруженість електричного поля в точці, що збігається з центром цього кільця.
3
Рис. 3.47
О
Дано
= 10 см τ
= 0,2 мкКл/м
= 120о
= ?
Визначимо напруженість електричного поля в точці де перетинаються вісі координат. Для цього знайдемо спочатку напруженість поля, що створюється зарядом :
(1)
де - радіус-вектор, спрямований від елемента до точки, у якій обчислюється напруженість.
Виразимо вектор через проекції і на осі координат: де та - одиничні вектори напрямків (орти). Напруженість знайдемо інтегруванням:
(2)
Інтегрування ведемо уздовж дуги довжиною . У силу симетрії . Тоді
, (3)
де Оскільки , то
(4)
Підставимо вираз у (3) і, взявши до уваги симетричне розташування дуги щодо осі Оу, межі інтегрування оберемо від 0 до /4, а результат подвоїмо:
![]() (5)
(5)
Підставляємо величини, які задані в умові задачі (виражені в одиницях системи СІ), у вираз (5) і отримуємо:
=
3.50. Кільце радіусом = 10 см заряджене з лінійною густиною заряду τ = 800 нКл/м. Визначити потенціал у точці, що розташована по осі кільця на відстані = 10 см від його центра.
3.50.
Дано
= 10 см τ
= 800 нКл/м
= 10 см
= ?
З
Рис. 3.50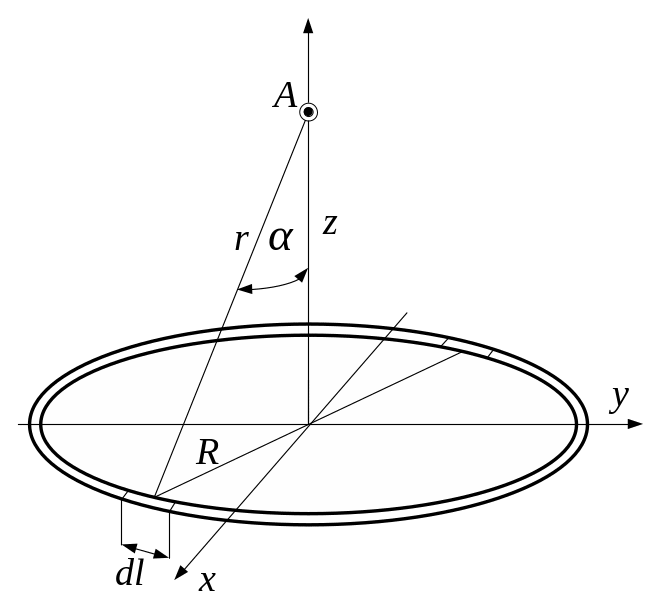
З'єднаємо координатну площину хОу з площиною кільця, а вісь Оz - із віссю кільця (рис. 3.50). На кільці виділимо малу ділянку довжиною . Оскільки заряд , що знаходиться на цій ділянці, можна вважати точковим, то потенціал електричного поля в точці А, що утворюється цим зарядом, може бути записаний у вигляді
![]() (1)
(1)
де
- радіус-вектор, направлений від елемента
до точки А
(). Як видно
з рис. 3.50
=
![]() .
.
Оскільки потенціал точки поля являє собою скалярну величину, то потенціал, який створює усе кільце, дорівнює алгебраїчній сумі потенціалів, створених всіма малими ділянками кільця, тобто:
![]() . (2)
. (2)
В отриманий вираз підставляємо величини, які задані в умові задачі (виражені в одиницях системи СІ) і отримаємо відповідь:
=
3.51. Електричне поле утворене нескінченно довгою зарядженою ниткою, лінійна густина заряду якої = 20 пКл/м. Визначити різницю потенціалів U двох точок поля, що відстоять від нитки на відстані r1 = .8 см і r2 = 12 см.
3
Рис. 3.51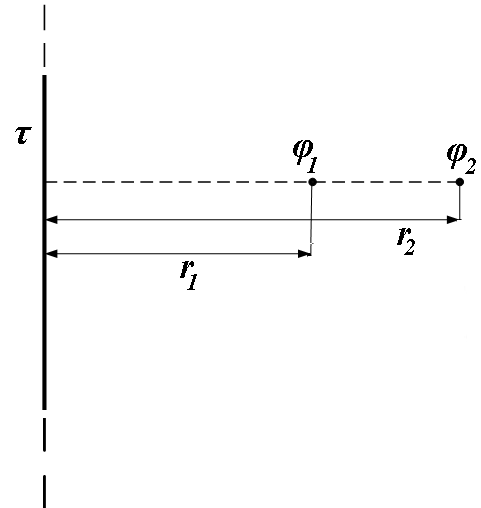
Дано
= 20 пКл/м
![]() = 8 см
= 8 см![]() = 12 см
= 12 см
![]() = ?
= ?
Зробимо малюнок, на якому вертикально зображена нескінченно довга заряджена нитка з лінійною густиною заряду τ.
Різницю потенціалів U двох точок поля, що відстоять від нитки на відстані r1 і r2,
можна визначити через напруженість в заданих точках за формулою:
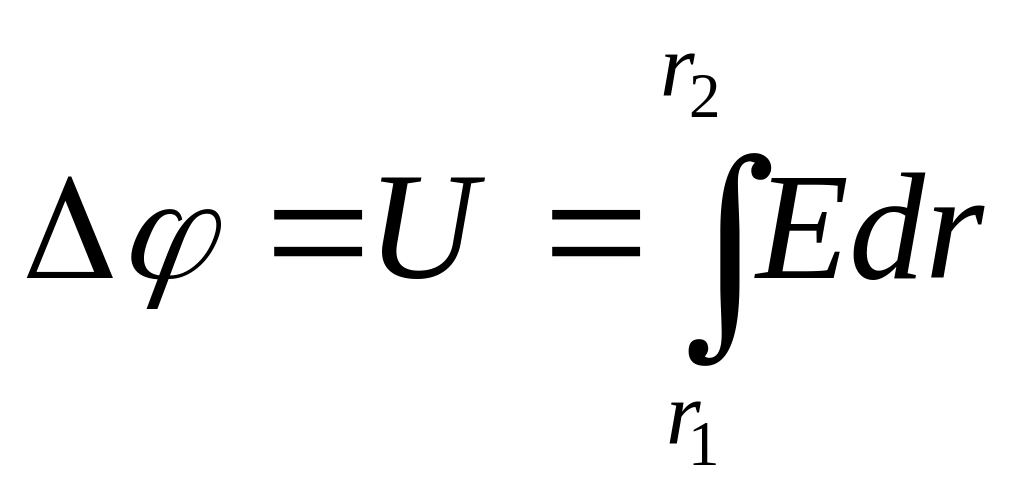 .
.
Напруженість електричного поля утвореного нескінченно довгою зарядженою ниткою визначається за формулою (18.18, в):
![]() ,
,
де
![]() = ………..
= ………..
Якщо виконати інтегрування, отримаємо
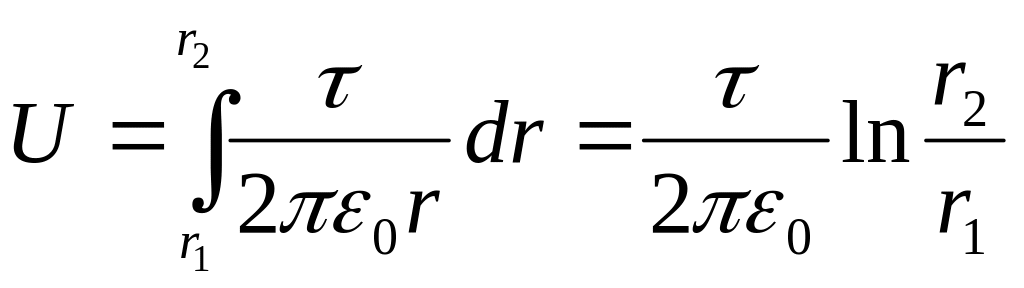 .
.
Зробимо підстановку заданих величин у системі СІ:
=
3.52. Тонка квадратна рамка рівномірно заряджена з лінійною густиною заряду = 200 пКл/м. Визначити потенціал φ поля в точці перетину діагоналей.
3
Рис. 3.52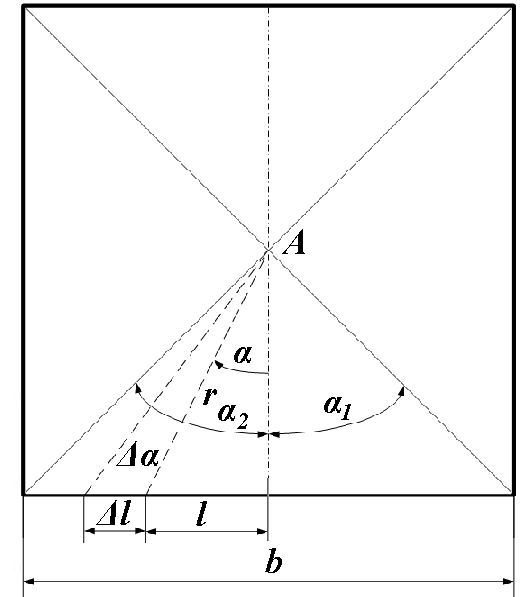
Дано
= 200 пКл/м
= ?
Зробимо малюнок,
на якому зображений елемент
![]() нижньої сторони рамки, заряд якого можна
вважати точковим. Для точкового заряду
маємо формулу потенціалу поля, яку і
застосуємо:
нижньої сторони рамки, заряд якого можна
вважати точковим. Для точкового заряду
маємо формулу потенціалу поля, яку і
застосуємо:
![]() , (1)
, (1)
де = 9∙109 м/Ф – коефіцієнт пропорційності, - відстань від точки, в якій визначається потенціал, до елемента .
З малюнка видно, що
![]() . (2)
. (2)
Диференціюємо цей вираз
![]() . (3)
. (3)
А відстань визначаємо з трикутника:
![]() . (4)
. (4)
Підставляємо вирази (3) і (4) у вираз (1)
![]() . (5)
. (5)
Інтегруючі вираз
(5) в межах від
![]() до
до
![]() ,
отримаємо потенціал, який створює одна
сторона квадрата
,
отримаємо потенціал, який створює одна
сторона квадрата
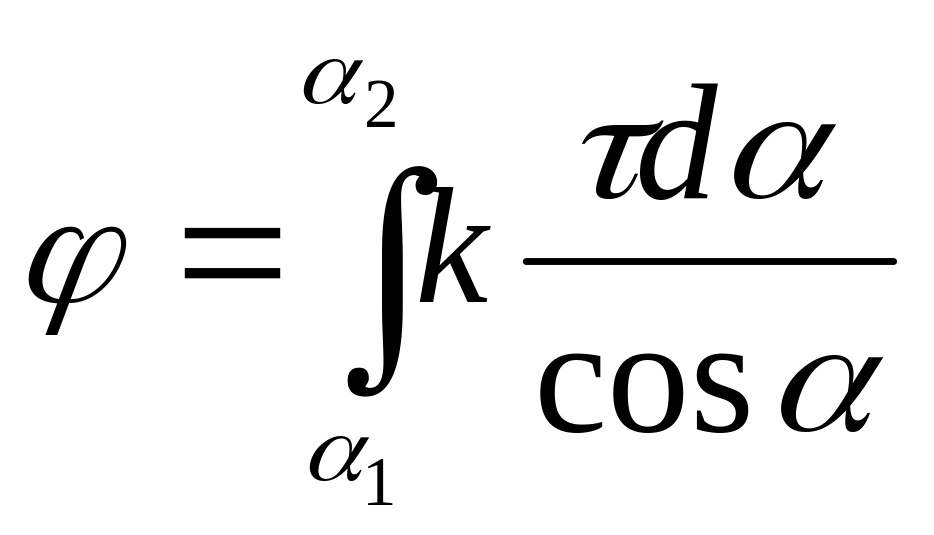 . (6)
. (6)
В силу симетрії точки відносно кінців сторони, маємо
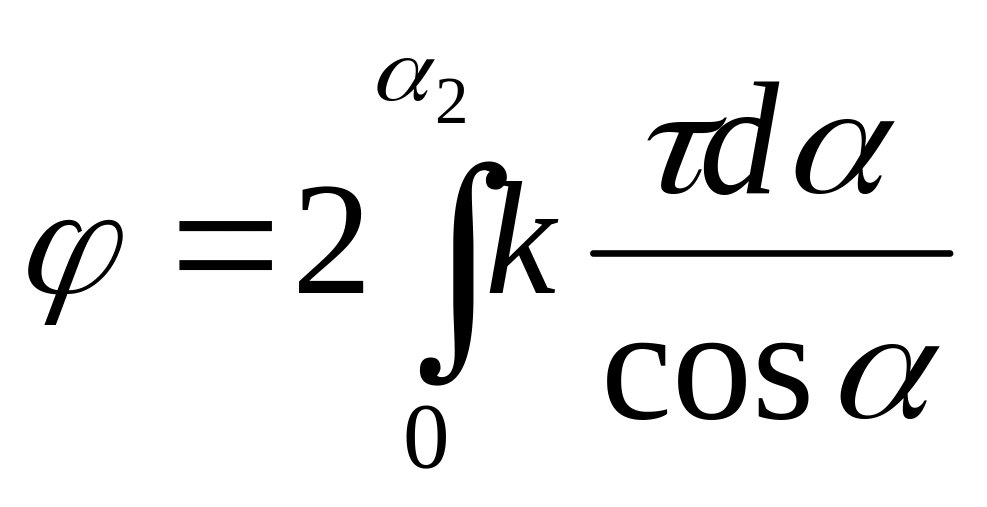 . (7)
. (7)
Так як
![]() .
Див. табл.. 27.
.
Див. табл.. 27.
Тоді для всіх сторін отримаємо
![]() .
.
Підставляємо границі інтегрування і числові значення:
=
3.53. На двох концентричних сферах радіусом R і 2R рівномірно розподілені заряди з поверхневою густиною σ1 і σ2. Обчислити напруженість Е електричного поля в точці, що відлучена від спільного центра сфер на відстань r. Побудувати графік залежності Е(r). Прийняти σ1 = 4σ, σ2 = σ, σ = 30 нКл/м2, r = 1,5R.
Рис. 3.53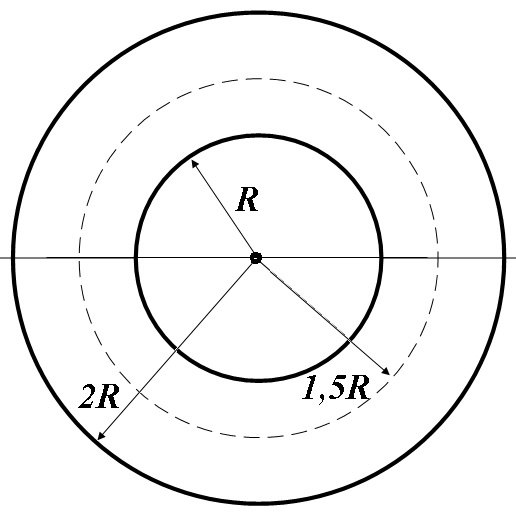
3.53.
Дано
= 30 нКл/м2
= ?
![]()
![]()
![]()
![]()
![]()
Зробимо малюнок, на якому зображені дві концентричні сфери радіусом R і 2R, по поверхні яких рівномірно розподілені заряди з поверхневою густиною σ1 і σ2.
Застосуємо теорему Гауса до вектора напруженості електричного поля:
1. Для
![]()
![]()
![]() (1)
(1)
2. Для
![]()
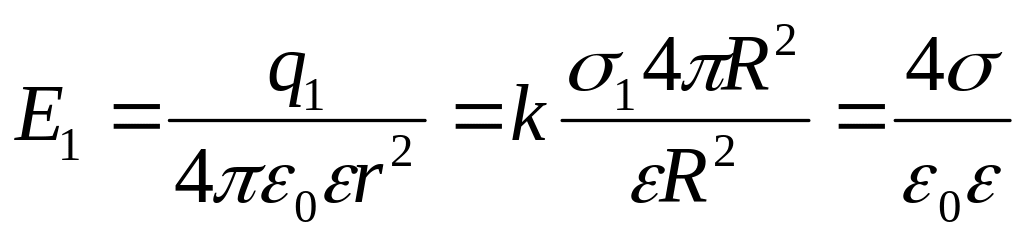 . (2)
. (2)
3. Для
![]()
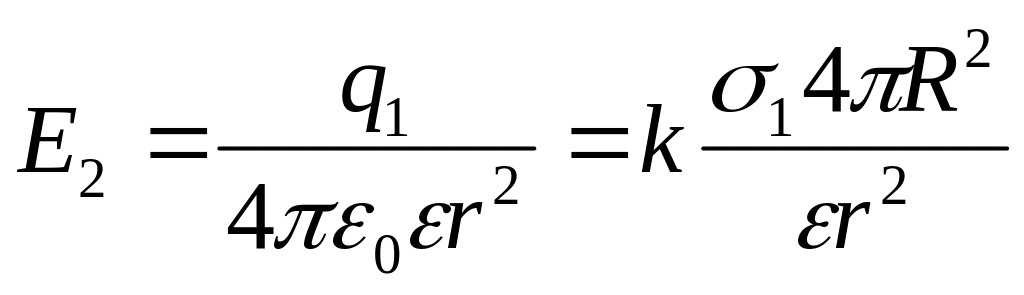 . (3)
. (3)
4. Для
![]() ,
але з внутрішньої сторони другої сфери
,
але з внутрішньої сторони другої сфери
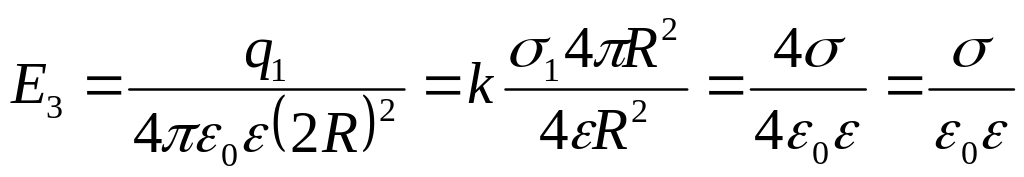 . (4)
. (4)
5. Для , але з зовнішньої сторони другої сфери
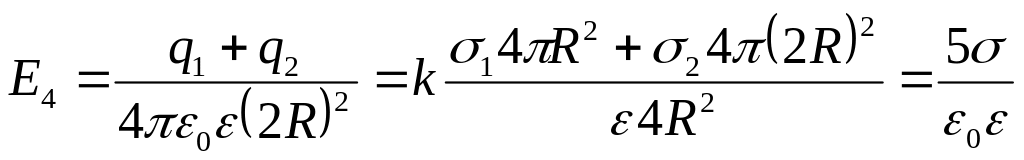 . (5)
. (5)
6
Рис. 3.53, а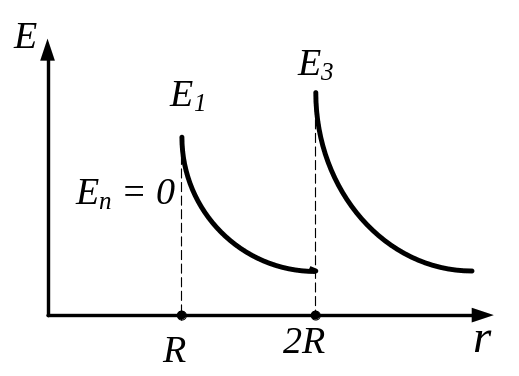
![]()
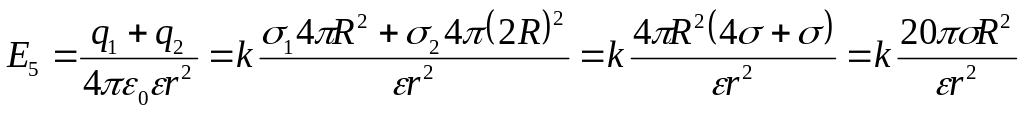 .
(6)
.
(6)
Будуємо графік залежності Е(r), використовуючи отримані вирази:
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.54. Дивись умову попередньої задачі. Прийняти σ1 = σ, σ2 = - σ, σ = 0,1 мкКл/м2, r = 3R.
Рис. 3.54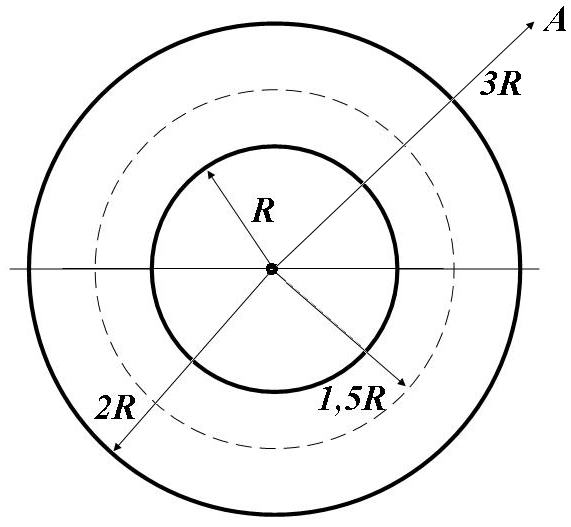
3.54.
Дано
= 0,1 мкКл/м2
= ?
![]()
![]()
![]()
Розв’язок.
Зробимо малюнок, на якому зображені дві концентричні сфери радіусом R і 2R, по поверхні яких рівномірно розподілені заряди з поверхневою густиною σ1 і σ2, та точка А, в якій визначатимемо напруженість електричного поля.
Застосуємо теорему Гауса до вектора напруженості електричного поля:
1. Для
(1)
2. Для
. (2)
3. Для
. (3)
4. Для , але з внутрішньої сторони другої сфери
. (4)
5. Для , але з зовнішньої сторони другої сфери
. (5)
6
Рис. 3.53, а
. (6)
Будуємо графік залежності Е(r), використовуючи отримані вирази:
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (6):
=
3.55. Чотири
однакових краплі ртуті, заряджені до
потенціалу
![]() = 10 В, зливаються в одну. Знайти потенціал
краплі, що утворилася?
= 10 В, зливаються в одну. Знайти потенціал
краплі, що утворилася?
3.55.
Дано
= 4
= 10 В
= ?
Під час злиття краплин в одну сталими залишаються їхні загальні заряд та об’єм:
![]() (1)
(1)
де - заряд великої краплі; , , - заряд, ємність і радіус малої краплі; - радіус великої краплі.
Потенціал великої краплі знаходимо за формулою
![]() . (2)
. (2)
Зробимо підстановку заданих величин: =
3.56. Дві паралельні заряджені площини, поверхнева густина заряду яких становить σ1 = 2 мкКл/м2 і σ2 = - 0,8 мкКл/м2, знаходяться на відстані = 0,6 см одна від одної. Визначити різницю потенціалів U між площинами.
3.56.
Дано
σ1
= 2 мкКл/м2 σ2
= - 0,8 мкКл/м2
= 0,6 см
= ?
Електростатичне поле між двома різнойменно зарядженими паралельними нескінченними площинами:
![]() . (1)
. (1)
Для однорідного поля (поля плоского конденсатора) напруженість
![]() ,
(2)
,
(2)
де U — різниця потенціалів між пластинами конденсатора; d — відстань між ними.
З формул (1) і (2) отримаємо:
![]()
Зробимо підстановку заданих величин:
=
3.57. На двох нескінченних паралельних площинах рівномірно розподілені заряди з поверхневою густиною σ1 і σ2 . Потрібно обчислити напруженість Е поля в точках розташованих ліворуч та праворуч від площин. Прийняти σ1 = 2σ, σ2 = - σ, σ = 20 нКл/м2.
3.57.
Рис. 3.57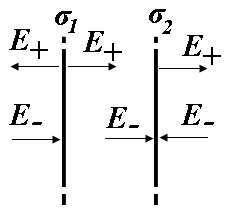
Дано
σ1
= 2σ σ2
= - σ σ
= 20 нКл/м2
![]() = ?,
= ?,
![]() = ?
= ?
Зробимо малюнок:
Електростатичне поле поза двома різнойменно зарядженими паралельними нескінченними площинами дорівнює:
![]() . (1)
. (1)
Зробимо підстановку заданих величин у системі СІ:
= =
воруч від площин. Прийняти σ1 = 2σ, σ2 = - σ, σ = 20 нКл/м2.
3.58. Заряд рівномірно розподілений по нескінченній площині з поверхневою густиною = 10нКл/м2. Визначити різницю потенціалів двох точок поля, одна з яких знаходиться на площині, а інша вилучена від її на відстань а = 10 см.
3.58.
Дано
= 10 нКл/м2 а
= 10 см
Рис. 3.58
![]() = ?,
= ?,
Зробимо малюнок:
Зв’язок між напруженістю та потенціалом поля:
![]() . (1)
. (1)
Звідки різниця потенціалів двох точок поля дорівнює
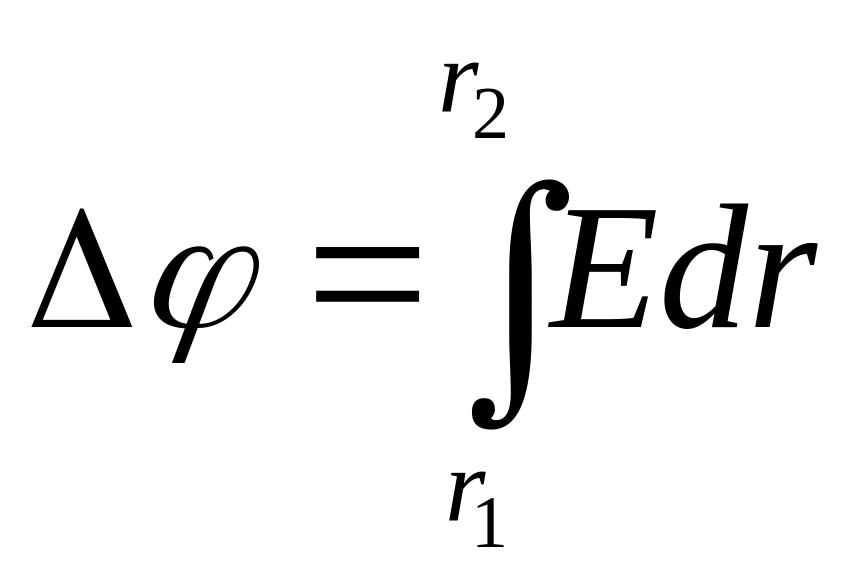 , (2)
, (2)
де - відстань від точки поля до площини.
Електростатичне поле рівномірно зарядженої нескінченної площини дорівнює:
![]() . (3)
. (3)
Підставимо (3) у (2) і виконаємо інтегрування
![]()
Зробимо підстановку заданих величин у системі СІ:
=
3.59. На двох коаксіальних нескінченних циліндрах радіусами R і 2R рівномірно розподілені заряди з поверхневою густиною σ1 і σ2. Обчислити напруженість Е поля в точці, що відстоїть від спільної осі циліндрів на відстані r. Побудувати графік залежності Е(r). Прийняти σ1 = - 2σ, σ2 = σ, σ = 50 нКл/м2, r = 1,5R.
Рис. 3.59
3.59.
Дано
σ1
= - 2σ
= 50 нКл/м2
= ?
Зробимо малюнок, на якому зображені два коаксіальних нескінченних циліндра радіусом R і 2R, по поверхні яких рівномірно розподілені заряди з поверхневою густиною σ1 і σ2.
Застосуємо теорему Гауса до вектора напруженості електричного поля, тоді її записують так:
1. Для
(1)
2. Для
![]() . (2)
. (2)
3
Рис. 3.59, а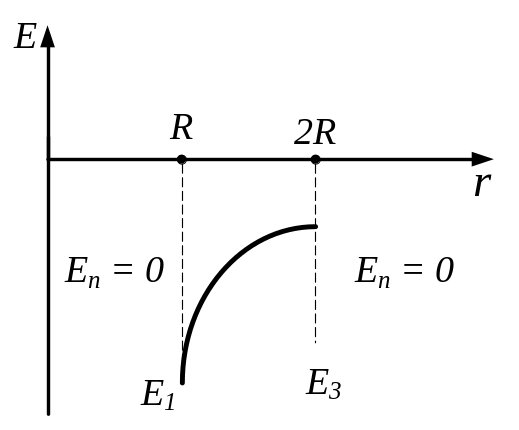
![]() . (3)
. (3)
4. Для , але з внутрішньої сторони другого циліндра
![]() . (4)
. (4)
5. Для , але з зовнішньої сторони другого циліндра
![]() . (5)
. (5)
6. Для отримаємо такий же результат.
Будуємо графік залежності Е(r) (див. рис. 3.59, а), використовуючи отримані вирази (1) - (5).
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.60. Дивись умову попередньої задачі. Прийняти σ1 = σ, σ2 = - σ, σ = 60 нКл/м2, r = 3R .
3.60.
Дано
σ1
= σ
= 60 нКл/м2
= ?
Рис. 3.60
Зробимо малюнок, на якому зображені два коаксіальних нескінченних циліндра радіусом R і 2R, по поверхні яких рівномірно розподілені заряди з поверхневою густиною σ1 і σ2.
Застосуємо теорему Гауса до вектора напруженості електричного поля, тоді для даного випадку її записують так:
1. Для
(1)
2. Для
![]() . (2)
. (2)
3. Для
![]() . (3)
. (3)
4. Для , але з внутрішньої сторони другого циліндра
![]() . (4)
. (4)
5. Для , але з зовнішньої сторони другого циліндра
![]() . (5)
. (5)
4
Рис. 2
![]() .
(6)
.
(6)
Будуємо графік залежності Е(r) (див. рис. 2), використовуючи отримані вирази (1) - (5).
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (6):
=
3.61. Яку
різницю потенціалів U
повинен пройти електрон, щоб одержати
швидкість
![]() = 8 Мм/с?
= 8 Мм/с?
3.61.
Дано
= 8 Мм/с
= ?
Електричне поле перемішуючі електричний заряд виконує роботу:
![]() , (1)
, (1)
де - заряд електрона, який дорівнює ………
Ця робота йде на зміну кінетичної енергії цього заряду:
![]() , (2)
, (2)
де - маса електрона, яка дорівнює ……..
Вважаючи початкову швидкість електрона рівною нулю, порівняємо рівняння (1) та (2) і отримаємо розрахункову формулу:
![]() . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.62. Кулька масою = 40 мг, яка має позитивний заряд q = 1 нКл, рухається з швидкістю = 10 см/с. На яку відстань може наблизитися кулька до позитивного точкового заряду q0 = 1,33 нКл?
3.62.
Дано
= 40 мг q
= 1 нКл
= 10 см/с q0
= 1,33 нКл
= ?
Будемо вважати, що позитивний точковий заряд q0 створює електричне поле, в якому рухається кулька втрачаючи свою кінетичну енергію, тобто електричне поле, гальмуючі кульку, виконує роботу:
![]() . (1)
. (1)
Різниця потенціалів поля, створеного зарядом кульки, дорівнює
![]() , (2)
, (2)
де
- коефіцієнт пропорційності, який
дорівнює
![]() м/Ф; а
м/Ф; а
![]() .
.
Ця робота йде на зміну кінетичної енергії цього заряду:
![]() , (3)
, (3)
вважаючи кінцеву
швидкість кульки рівною нулю(![]() = 0), порівняємо рівняння (1) та (3) і отримаємо
розрахункову формулу:
= 0), порівняємо рівняння (1) та (3) і отримаємо
розрахункову формулу:
![]() . (4)
. (4)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (4):
=
3.63. До якої відстані можуть зблизитися два електрони, якщо вони рухаються назустріч один одному з відносною швидкістю = 106 м/с?
3.63.
Дано
= 9,1∙10-31
кг q
= 1,6-10-19
Кл
= 106
м/с
= ?
Будемо вважати, що один електрон створює електричне поле, в якому рухається другий з початковою швидкістю втрачаючи свою кінетичну енергію, тобто електричне поле, гальмуючі електрон, виконує роботу:
. (1)
Різниця потенціалів поля, створеного зарядом першого електрон, дорівнює
![]() , (2)
, (2)
де - коефіцієнт пропорційності, який дорівнює м/Ф; а .
Ця робота йде на зміну кінетичної енергії електрона:
![]() , (3)
, (3)
вважаючи кінцеву швидкість електрона рівною нулю( = 0), порівняємо рівняння (1) та (3) і отримаємо розрахункову формулу:
![]() . (4)
. (4)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (4):
=
3.64. Дві кульки з зарядами q1 = 6,66 нКл і q2 = 13,33 нКл знаходяться на відстані d = 40 см. Яку роботу А треба виконати, щоб зблизити їх до відстані D = 25 см?
3.64.
Дано
q1
= 6,66 нКл q2
= 13,33 нКл q
= 1,6-10-19
Кл d
= 40 см D
= 25 см
А = ?
Будемо вважати, що одна кулька створює електричне поле, в якому рухатиметься друга, тоді виконана робота дорівнює:
![]() . (1)
. (1)
Різниця потенціалів поля, створеного зарядом першої кульки, дорівнює
![]() , (2)
, (2)
де - коефіцієнт пропорційності, який дорівнює м/Ф; а .
Тоді робота дорівнює:
![]() , (3)
, (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
А =
3.65. Яка робота здійснюється при перенесенні точкового заряду q = 20 нКл з нескінченності в точку, що знаходиться на відстані 1 см від поверхні кулі радіусом R = 1 см з поверхневою густиною заряду σ = 10 мкКл/м2?
3.65.
Дано
q = 20 нКл
d
= 1 см
= 1 см σ
= 10 мкКл/м2
А = ?
З
Рис. 3.65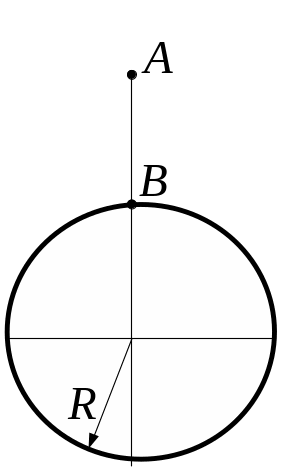
Потенціал у даній точці електричного поля
![]() .
(1)
.
(1)
де
![]() - робота по переміщенню пробного заряду
із нескінченності у дану точку полю;
- заряд, який переміщають.
- робота по переміщенню пробного заряду
із нескінченності у дану точку полю;
- заряд, який переміщають.
З формули (1) робота, яка здійснюється при перенесенні точкового заряду q, дорівнює:
![]() . (2)
. (2)
Потенціал кулі в точці А знаходимо по формулі для точкового заряду:
![]() , (3)
, (3)
де
![]() - заряд кулі,
- заряд кулі,
![]() - відстань від центра кулі, куди ми умовно
поміщаємо її заряд, до т. А.
- відстань від центра кулі, куди ми умовно
поміщаємо її заряд, до т. А.
Тоді робота дорівнює:
![]() . (4)
. (4)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (4):
А =
3.66. Кулька масою 1 г і зарядом 10 нКл переміщується з точки і, потенціал якої φ1 = 600 В, в точку 2, потенціал якої φ2 = 0. Знайти швидкість кульки в точці 1, якщо в точці 2 вона стала рівною 2 = 20 см/с.
3.66.
Дано
= 1 г q
= 10 нКл φ1
= 600 В φ2
= 0
2
= 20 см/с
![]() = ?
= ?
Будемо вважати,
що куля рухається з початковою швидкістю
![]() ,
при цьому збільшує свою кінетичну
енергію, тобто електричне поле виконує
роботу:
,
при цьому збільшує свою кінетичну
енергію, тобто електричне поле виконує
роботу:
, (1)
де
![]() - різниця потенціалів
- різниця потенціалів
Ця робота йде на зміну кінетичної енергії кулі:
![]() , (2)
, (2)
З рівнянь (1) та (2) отримаємо
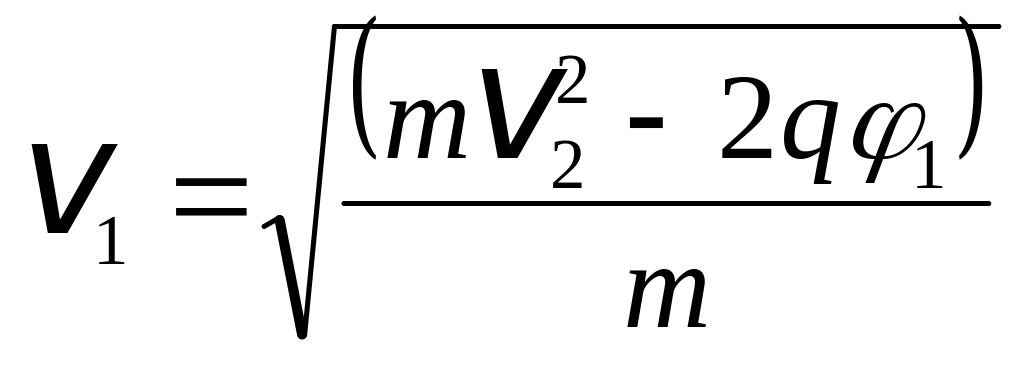 . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.67. На відстані d1 = 4 см від нескінченно довгої, зарядженої нитки знаходиться точковий заряд q = 0,66 нКл. Під дією електричного поля заряд наближається до нитки на відстань d2 = 2 см. При цьому здійснюється робота А = 5 10-6 Дж. Знайти лінійну густину заряду на нитці.
3.67.
Дано
d1
= 4 см q
= 0,66 нКл
d2
= 2 см А
= 5 10-6
Дж
= ?
Електричне поле виконує роботу проти змінної сили:
![]() , (1)
, (1)
де - різниця потенціалів двох точок поля, яку визначаємо за формулою:
, (2)
де напруженість поля, яке створює заряджена нитка в точці простору дорівнює
![]() . (3)
. (3)
Підставимо вираз (3) у формулу (2) і виконавши інтегрування отримаємо
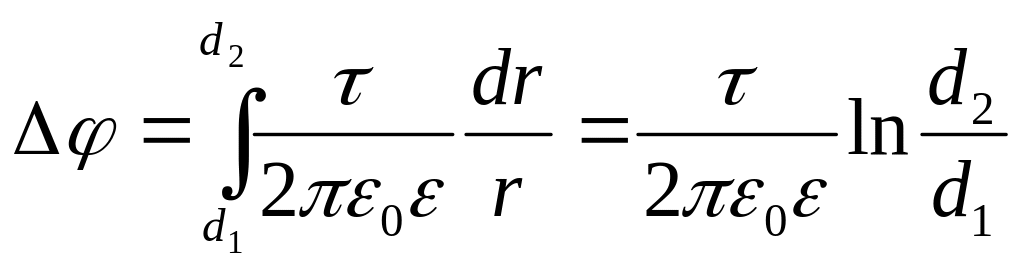 . (4)
. (4)
Тоді робота дорівнюватиме:
![]() , (5)
, (5)
З рівняння (5) отримаємо формулу для розрахунку лінійної густини заряду на нитці:
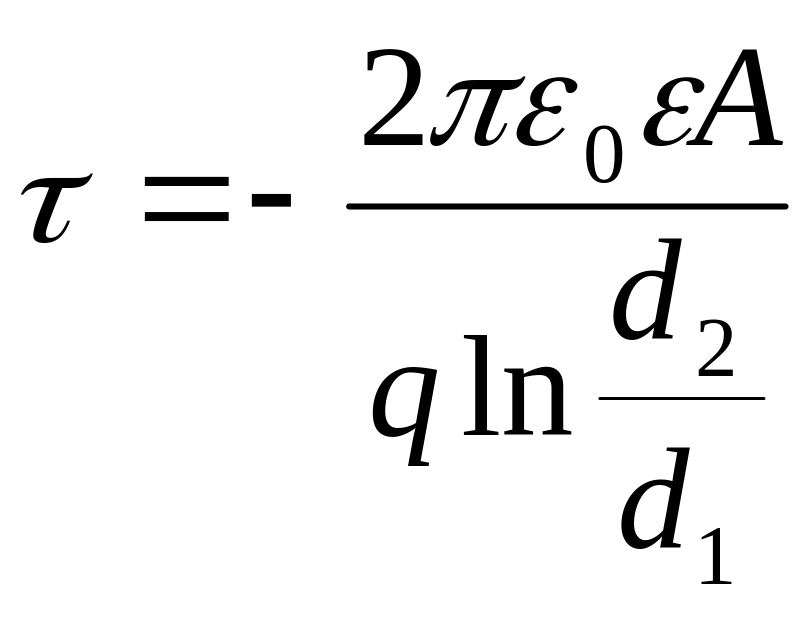 . (6)
. (6)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (6):
=
3.68. Електричне поле утворене позитивно зарядженою нескінченно довгою ниткою. Рухаючись під дією цього поля від точки, що знаходиться на відстані L1 = 1 см від нитки, до точки L2 = 4 см, α - частинка змінила свою швидкість від 1 = 2 105 м/с до швидкості 2 = 3 106 м/с. Знайти лінійну густина заряду на нитці.
3.68.
Дано
L1
= 1 см L2
= 4 см q
= 3,2∙10-19
Кл
1
= 2 105 м/с
2
= 3 106
м/с
= ?
Електричне поле виконує роботу проти змінної сили:
![]() , (1)
, (1)
де - різниця потенціалів двох точок поля, яку визначаємо за формулою:
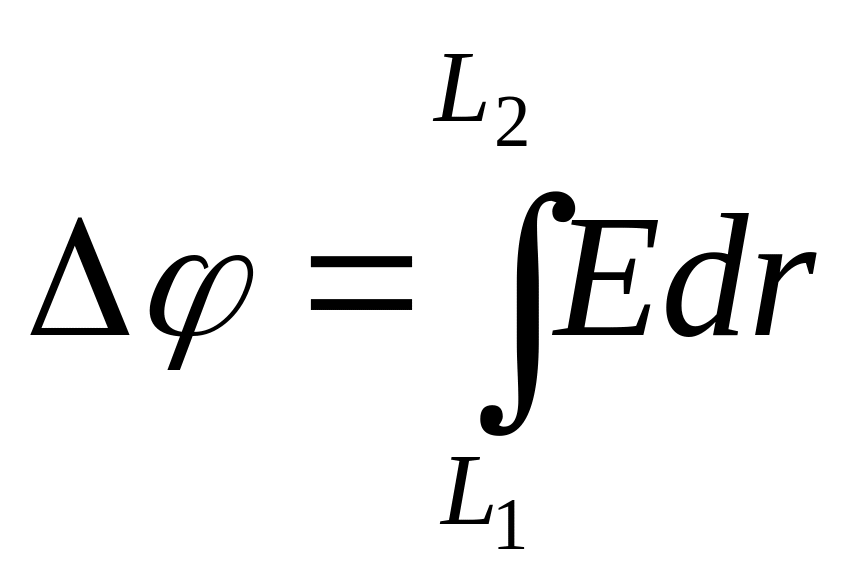 , (2)
, (2)
де напруженість поля, яке створює заряджена нитка в точці простору дорівнює
. (3)
Підставимо вираз (3) у формулу (2) і виконавши інтегрування отримаємо
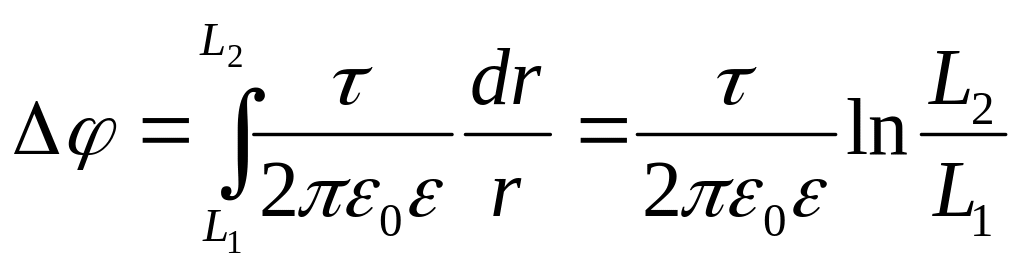 . (4)
. (4)
Тоді робота дорівнюватиме:
![]() , (5)
, (5)
Ця робота йде на зміну кінетичної енергії кулі:
, (6)
де - маса -частинки.
З рівнянь (5) та (6) отримаємо
![]() . (7)
. (7)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (7):
=
3.69. Електричне поле утворене позитивно зарядженою нескінченно довгою ниткою з лінійною густиною заряду τ = 0,2 мкКл/м. Яку швидкість отримає електрон під дією поля, наблизившись до нитки з відстані L1 = 1 см до відстані L2 = 0,5 см?
3.69.
Дано
τ = 0,2 мкКл/м L1
= 1 см L2
= 0,5 см q
= - 1,6∙10-19
Кл
1
= 0
2
= ?
Електричне поле виконує роботу проти змінної сили:
, (1)
де - різниця потенціалів двох точок поля, яку визначаємо за формулою:
, (2)
де напруженість поля, яке створює заряджена нитка в точці простору, дорівнює
. (3)
Підставимо вираз (3) у формулу (2) і виконавши інтегрування отримаємо
. (4)
Тоді робота дорівнюватиме:
, (5)
Ця робота йде на зміну кінетичної енергії:
![]() ,
де
- маса електрона. (6)
,
де
- маса електрона. (6)
З рівнянь (5) та (6) отримаємо
![]() . (7)
. (7)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (7):
2 =
3.70. Біля зарядженої нескінченної площини знаходиться точковий заряд q = 0,66 нКл. Заряд переміщається по лінії напруженості поля на відстань d = 2 см; при цьому здійснюється робота 5 10-6 Дж. Знайти поверхневу густина заряду σ на площині.
3.70.
Дано
q = 0,66 нКл
d
= 2 см А
= 5 10-6
Дж
= ?
Електричне поле виконує роботу проти змінної сили:
![]() , (1)
, (1)
де - різниця потенціалів двох точок поля, яку визначаємо за формулою:
![]() , (2)
, (2)
де напруженість поля, яке створює заряджена нескінченна площина в точці простору, дорівнює
. (3)
Підставимо вираз (3) у формулу (2) і виконавши інтегрування отримаємо
![]() . (4)
. (4)
Тоді робота дорівнюватиме:
![]() , (5)
, (5)
З рівнянь (5) отримаємо
![]() . (6)
. (6)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (6):
=
3.71. Відстань між пластинами плоского конденсатора 4 см. Електрон починає рухатися від негативної пластини в той момент, коли від позитивної пластини Починає рухатися протон. На якій відстані від позитивної пластини вони зустрінуться?
3
Рис. 3.71
Дано
d = 4 см
= ?
Зробимо малюнок:
Вважаючи поле в конденсаторі однорідним, запишемо шлях, який пройдуть частинки до зустрічі, рухаючись з постійним прискоренням без початкової швидкості:
 (1)
(1)
З відношення рівнянь цієї системи отримаємо
![]() , (2)
, (2)
де
![]() = 1,6∙10-19
Кл – заряд електрона;
= 9,1∙10-31
кг - маса електрона;
= 1,6∙10-19
Кл – заряд електрона;
= 9,1∙10-31
кг - маса електрона;
![]() = 1,67∙10-27
кг – маса протона.
= 1,67∙10-27
кг – маса протона.
Розв’язуємо останнє рівняння відносно :
= (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.72. Відстань між пластинами плоского конденсатора 1 см. Від однієї з пластин одночасно починають рухатися протон і α-частинка. Яку відстань пройде α-частинка за той час, протягом якого протон пройде весь шлях від однієї пластини до іншої?
3.72.
Дано
d = 1 см
=
= ?
![]() =
=
![]() =
=
![]() =
=
Зробимо малюнок:
Вважаючи поле в конденсаторі однорідним, запишемо шлях, який пройдуть частинки до зустрічі, рухаючись з постійним прискоренням без початкової швидкості:
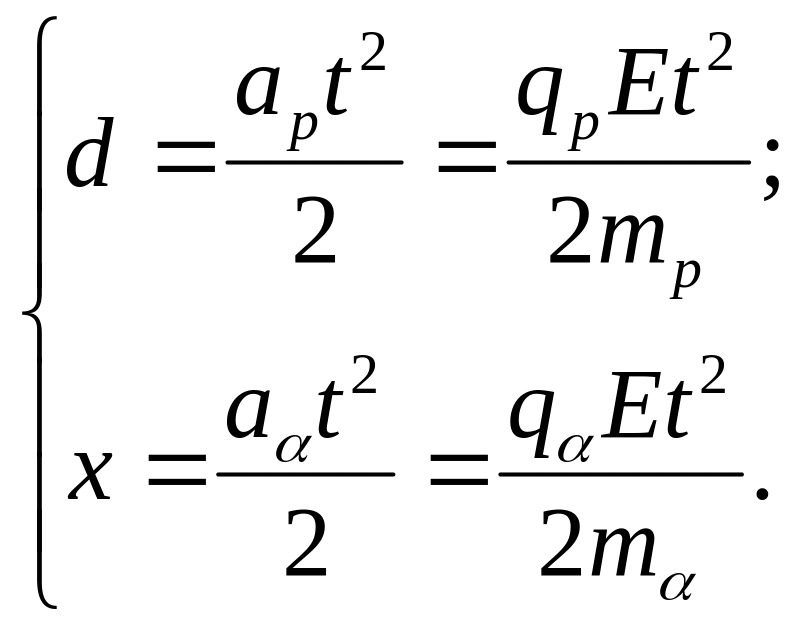 (1)
(1)
З відношення рівнянь цієї системи отримаємо
![]() . (2)
. (2)
Розв’язуємо останнє рівняння відносно :
= (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.73. Електрон, пройшовши в плоскому конденсаторі шлях від однієї пластини до іншої, набув швидкість = 108 м/с. Відстань між пластинами d = 5,3 мм. Знайти різницю потенціалів між пластинами і поверхневу густину заряду на пластинах.
3
Дано
d = 5,3 мм
=
=
= 108 м/с
= ?
= ?
Розв’язок.
Електричне поле виконує роботу по переміщенні електрона:
![]() , (1)
, (1)
Ця робота йде на зміну кінетичної енергії:
![]() ,
де
,
де
![]() - маса електрона, а
= 0 (2)
- маса електрона, а
= 0 (2)
З рівнянь (1) і (2) отримаємо
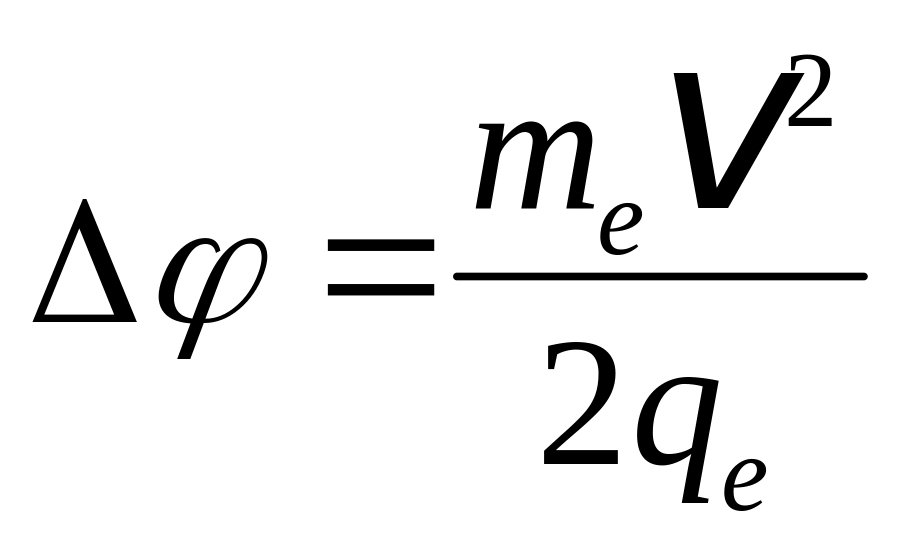 . (3)
. (3)
Напруженість поля в конденсаторі визначається формулою:
![]() . (4)
. (4)
З (4) визначаємо поверхневу густину заряду на пластинах конденсатора
![]() . (5)
. (5)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вирази (3) і (5):
= =
3.74. Електричне поле утворене двома паралельними пластинами, що знаходяться на відстані 2 см одна від одної. До пластин прикладена різниця потенціалів U щ 120 В. Яку швидкість отримає електрон під дією поля, пройшовши по лінії напруженості відстань h = 3 мм?
3.74.
Дано
d = 2 см U
= 120 В
=
=
h
= 3 мм
= ?
Однорідне електричне поле виконує роботу по переміщенні електрона:
![]() , (1)
, (1)
де напруженість поля в конденсаторі пов’язана з різницею потенціалів на його пластинах рівнянням:
![]() . (2)
. (2)
Ця робота йде на зміну кінетичної енергії:
![]() , (3)
, (3)
де - маса електрона, а = 0.
З рівнянь (1), (2) і (3) отримаємо
![]() . (4)
. (4)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (4):
=
3.75. Електрон влітає в плоский горизонтально розташований конденсатор паралельно пластинам зі швидкістю 0 = 9 106 м/с. Різниця потенціалів між пластинами 100 В; відстань між пластинами 1 см. Знайти повне а, нормальне аn, і тангенціальне aτ прискорення електрона через 10 нc після початку його руху в конденсаторі.
Рис.
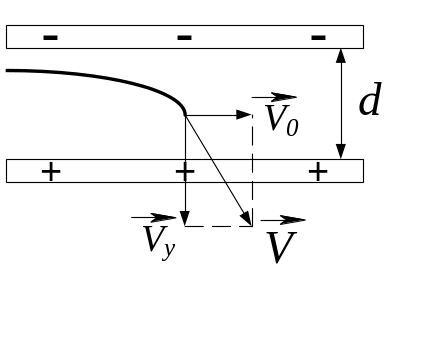
3.75.
Дано
0
= 9 106
м/с d
= 1 см U
= 100 В
=
=
= ?
![]() = 10 нс
= 10 нс
![]() = ?
= ?
![]() = ?
= ?
Зробимо малюнок:
Повне прискорення електрона визначаємо з формули закону Ньютона:
![]() . (1)
. (1)
Вертикальну складову швидкості електрона знаходимо з формули:
![]() . (2)
. (2)
Повна швидкість електрона дорівнює
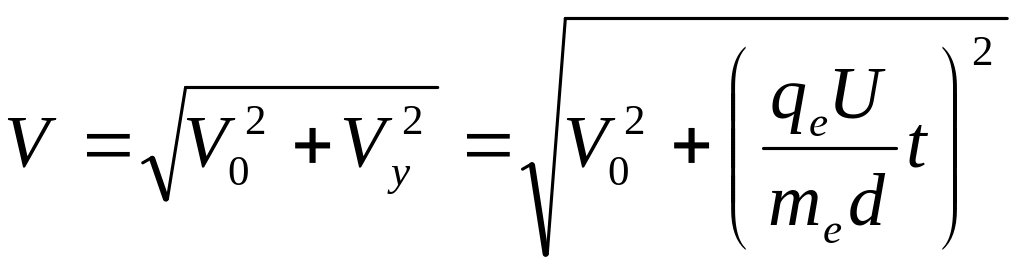 . (3)
. (3)
Тоді тангенціальне прискорення знаходимо за формулою:
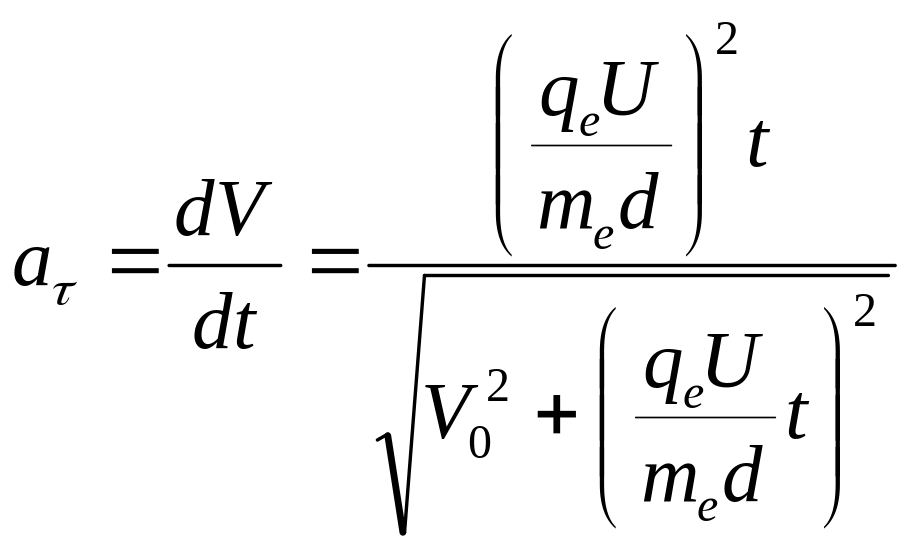 . (4)
. (4)
Тоді нормальне прискорення знаходимо за формулою:
![]() . (5)
. (5)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вирази (1), (4) і (5): =
= =
3.76. Електрон влітає в плоский горизонтально розташований конденсатор паралельно його пластинам з швидкістю 0 = 106 м/с. Напруженість поля в конденсаторі Е = 10 кВ/м; довжина конденсатора 5 см. Знайти модуль швидкості електрона при вильоті його з конденсатора.
3.76.
Дано
0
= 9 106
м/с Е
= 10 кВ/м
= 5 см
=
=
= ?
З
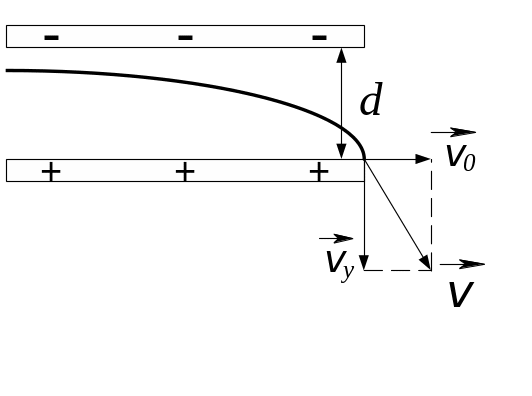
Вертикальну складову швидкості електрона знаходимо з формули:
![]() . (1)
. (1)
Повна швидкість електрона дорівнює
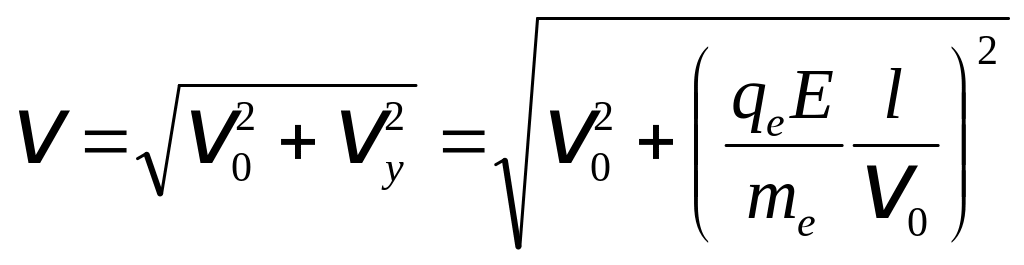 . (2)
. (2)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (2):
=
3.77. Електричне поле створене зарядженою провідною кулею, потенціал φ якої 300 В. Визначити роботу, яку треба виконати для переміщення заряду Q = 0,2 мкКл з точки 1 в точку 2 (див. рис. 3.77 ).
3.77.
Дано
φ = 300 В Q
= 0,2 мкКл
А = ?
З
Рис. 3.77
Електричне поле виконує роботу по переміщенні заряду:
![]() , (1)
, (1)
Різницю потенціалів поля, яке створюється кулею, визначаємо за формулою:
![]() , (2)
, (2)
де
= 2
,
а
= 4
;
![]() - заряд кулі.
- заряд кулі.
Тоді робота дорівнює
![]() . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
А =
3.78. Диполь з електричним моментом р = 100 пКл∙м вільно встановився у електричному полі напруженістю Е = 200 кв/м. Визначити роботу зовнішніх сил, яку необхідно виконати для повороту диполя на кут α = 180°.
3.78.
Дано
р = 100 пКл∙м Е
= 200 кв/м α
= 180°
А = ?
З
Рис. 3.78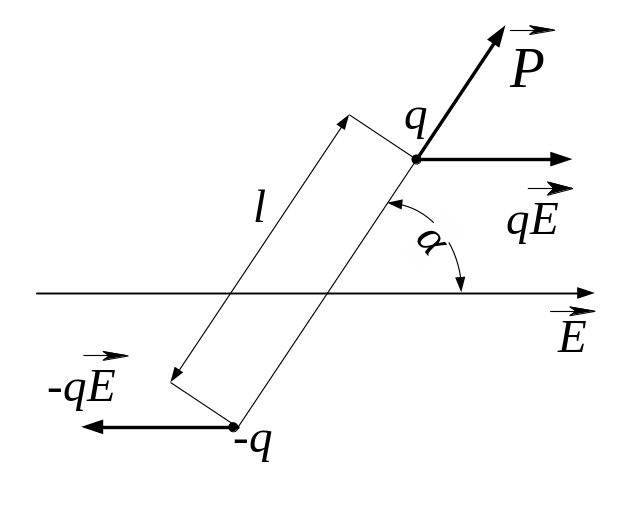
Елементарна робота
![]() під час повороту диполя на кут
під час повороту диполя на кут
![]() виражається формулою
виражається формулою
![]() , (1)
, (1)
де
![]() - механічний момент пари сил Кулона.
- механічний момент пари сил Кулона.
Повна робота при повороті від 0 до кута
![]() . (2)
. (2)
Виконавши інтегрування, отримаємо
![]() . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
А =
3.79. Порошина масою m = 200 мкг, що несе на собі заряд Q = 40 нКл, залетіла в електричне поле в напрямку силових ліній. Після проходження різниці потенціалів у 200 В порошина мала швидкість 10 м/с. Визначити швидкість порошини до того, як вона влетіла в поле.
3.79.
Дано
m = 200 мкг
Q
= 40 нКл
= 200 В
2
= 10 м/с
![]() = ?
= ?
Електричне поле виконує роботу по переміщенню порошини:
![]() , (1)
, (1)
Ця робота йде на зміну кінетичної енергії:
![]() . (2)
. (2)
Початкову швидкість порошини визначаємо з рівнянь (1) і (2):
![]() . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3
Рис. 3.80
3. 80.
Дано
Q1
= 2 мкКл Q2
= - 2 мкКл
= 10 см Q
= 0,5 мкКл
= ?
Електричне поле виконує роботу проти змінної сили:
, (1)
де - різниця потенціалів двох точок поля, які визначаємо за формулами:
![]() . (2)
. (2)
Вирази (2) підставляємо в(1)
![]() . (3)
. (3)
Підставимо вираз (3) у формулу (1) і зробимо підстановку заданих величин у системі СІ в отриманий вираз: =
3.81. Електрон, що мав кінетичну енергію Т = 10 еВ, залетів в однорідне електричне поле в напрямку силових ліній. Яку швидкість буде мати електрон, пройшовши в цьому полі різницю потенціалів U = 8 В?
3
Дано
Т = 10 еВ U
= 8 В
=
=
![]() = ?
= ?
Розв’язок.
Електричне поле виконує роботу по переміщенні електрона:
![]() , (1)
, (1)
Ця робота йде на зміну кінетичної енергії:
![]() , (2)
, (2)
де - маса електрона; - заряд електрона.
З рівнянь (1) і (2) отримаємо
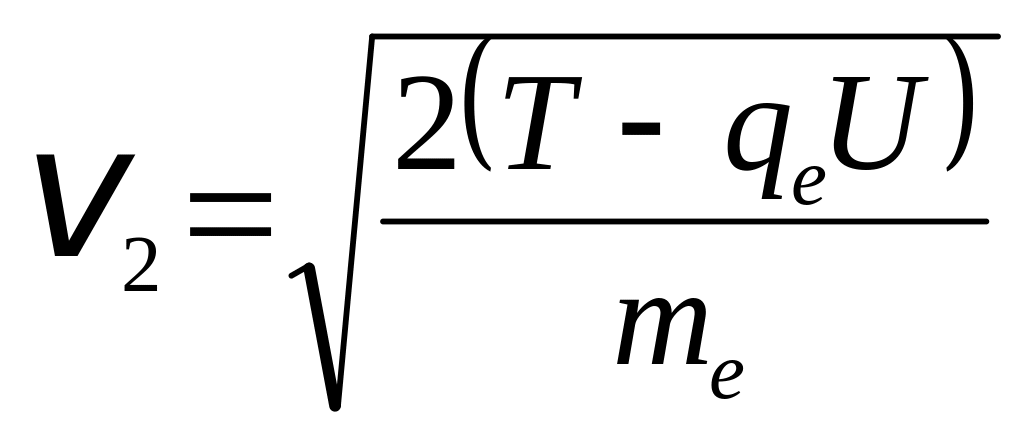 . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.82. Електрон, пройшовши в плоскому конденсаторі шлях від однієї пластини до іншої, придбав швидкість = 105 м/с. Відстань між пластинами d = 8 мм. Знайти різницю потенціалів U між пластинами та поверхневу густину заряду σ на пластинах.
3.82.
Дано
= 105 м/с d
= 8 мм U
= 120 В
=
=
= ?,
= ?
Однорідне електричне поле виконує роботу по переміщенні електрона:
![]() . (1)
. (1)
Ця робота йде на зміну кінетичної енергії:
, (2)
де
- маса електрона, а
![]() = 0.
= 0.
З рівнянь (1) і (2) отримаємо
. (3)
Напруженість поля в конденсаторі пов’язана з різницею потенціалів на його пластинах рівнянням:
![]() . (4)
. (4)
З теореми Гауса випливає, що напруженість поля між двома різнойменно зарядженими паралельними нескінченними площинами:
![]() . (5)
. (5)
З рівнянь (4) і (5) отримаємо
. (6)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вирази (3) і (6):
= =
3.83. Порошина масою 5 нг, що несе на собі 10 електронів, пройшла у вакуумі різницю потенціалів у 1 MB. Знайти кінетичну енергію порошини? Яку швидкість набула порошина?
3.83.
Дано
m = 5 нг
= 10
= 1 MB
=
=
![]() = ?,
= ?,
![]() = ?
= ?
Електричне поле виконує роботу по переміщенню порошини:
![]() . (1)
. (1)
Ця робота йде на зміну кінетичної енергії:
![]() . (2)
. (2)
З рівнянь (1) і (2) отримаємо зміну кінетичної енергії порошини:
![]() , (3)
, (3)
а також швидкість V, яку набула порошина
![]() . (4)
. (4)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ в вирази (3) і (4):
= =
3.84. Яку мінімальну швидкість повинен мати протон, щоб він міг досягти поверхні зарядженої до потенціалу φ = 400 В металевої кулі (див. рис. 3.84)?
3.84.
Дано
m = 5 нг
= 10 φ1
= 400 В
= ?
![]() =
=
![]() =
=
З
Рис. 3.84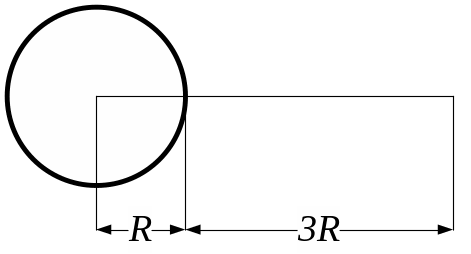
Електричне поле виконує роботу по гальмуванню протона:
![]() , (1)
, (1)
де різниця потенціалів дорівнює
![]() . (2)
. (2)
Потенціал точки поля , створеного металевою кулею дорівнює
![]() , (3)
, (3)
де - заряд кулі, який дорівнює
![]() . (4)
. (4)
Підставляємо вираз (4) у (3)
![]() ,
,
а отримане значення формулу (2):
![]() . (5)
. (5)
Робота, що визначається формулою (1), йде на зменшення кінетичної енергії протона до нуля:
![]() . (6)
. (6)
З рівнянь (1) і (6) отримаємо мінімальну швидкість, яку повинен мати протон, щоб він міг досягти поверхні зарядженої кулі:
![]() . (7)
. (7)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ в вираз (7):
=
3.85. В однорідне електричне поле напруженістю Е = 200 В/м влітає (уздовж силової лінії) електрон зі швидкістю 0 = 2 Мм/с. Визначити відстань, яку він подолає до того, як його швидкість зменшиться вдвічі.
3.85.
Дано
Е = 200 В/м V0
= 2 Мм/с
=
=
![]()
![]() = ?,
= ?,
Однорідне електричне поле виконує роботу по гальмуванню електрона:
![]() . (1)
. (1)
Ця робота йде на зміну кінетичної енергії:
![]() , (2)
, (2)
де - маса електрона.
З рівнянь (1) і (2) отримаємо
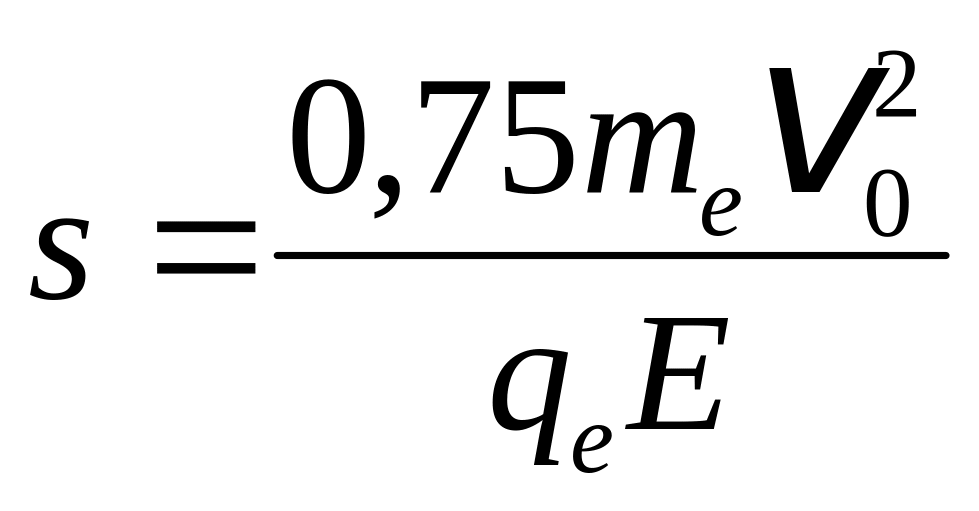 . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.86. Електрон рухається уздовж силової лінії однорідного електричного поля. У деякій точці поля з потенціалом φ1 = 100 В електрон мав швидкість 1 = 6 Мм/с. Визначити потенціал φ2 точки поля, дійшовши до який електрон втратить половину своєї швидкості.
3.86.
Дано
φ1
= 100 В
1
= 6 Мм/с
=
=
![]()
![]() = ?,
= ?,
Однорідне електричне поле виконує роботу по гальмуванню електрона:
![]() . (1)
. (1)
Ця робота йде на зміну кінетичної енергії:
![]() , (2)
, (2)
де - маса електрона.
З рівнянь (1) і (2) отримаємо
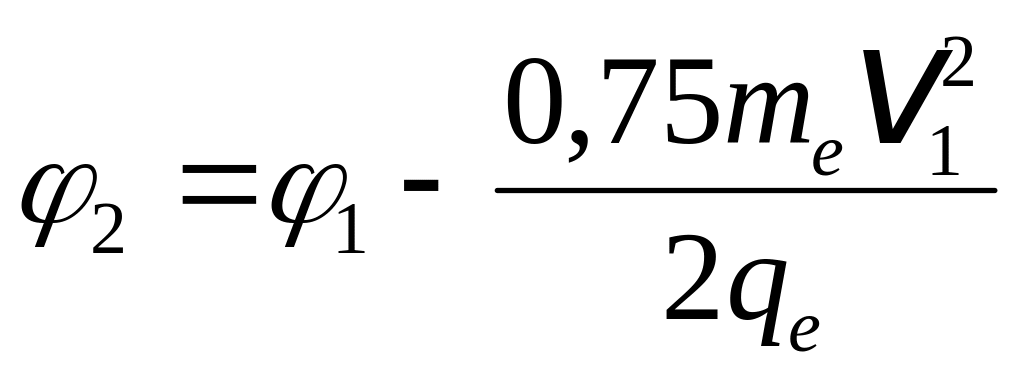 . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.87. Два заряди Q1 = 6 нКл і Q2 = 3 нКл знаходяться на відстані 60 см один від одного. Яку роботу необхідно виконати, щоб зменшити відстань між зарядами вдвічі?
3
Рис. 3.87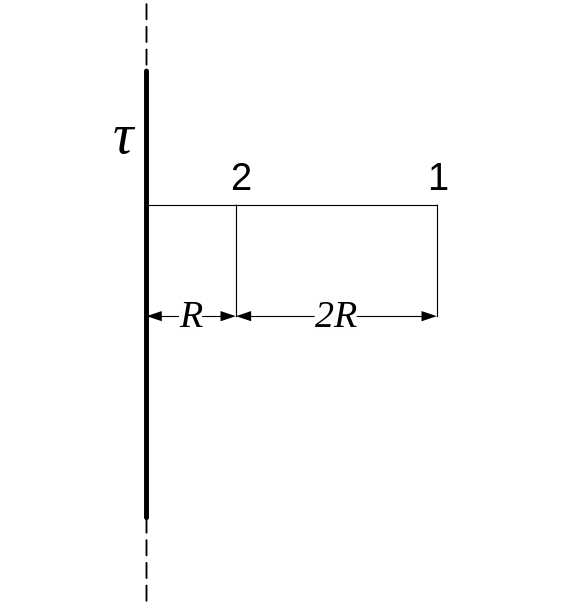
Дано
Q1
= 6 нКл Q2
= 3 нКл Q2
= - 2 мкКл
= ?
![]() = 60 см
= 60 см![]() = 0,5
= 0,5
Будемо вважати, що перший заряд створює електричне поле, в якому рухається другий заряд, тобто електричне поле виконує роботу:
![]() . (1)
. (1)
Різниця потенціалів поля, створеного першим зарядом, дорівнює
![]() , (2)
, (2)
де - коефіцієнт пропорційності, який дорівнює м/Ф; а .
Підставимо вираз (2) у формулу (1) і зробимо підстановку заданих величин у системі СІ в отриманий вираз:
=
3.88. Електричне поле створене нескінченною зарядженою ниткою з рівномірно розподіленим зарядом (τ = 10 нКл/м). Визначити кінетичну енергію Т2 електрона в точці 2, якщо в точці 1 його кінетична енергія становила Т1 = 200 еВ (див. рис.3.88).
3.88.
Розв’язок.
Дано
τ = 10 нКл/м Т1
= 200 еВ
=
![]() = ?,
= ?,
Електричне поле виконує роботу по переміщенню електрона:
![]() . (1)
. (1)
Зв’язок між напруженістю та потенціалом поля:
. (2)
Звідки різниця потенціалів двох точок поля дорівнює
![]() . (3)
. (3)
Теорему Гауса можна застосувати і до вектора напруженості електричного поля, тоді ЇЇ для нескінченно довгої зарядженої нитки записують так:
![]() . (4)
. (4)
З виразу (4) отримаємо
![]() . (5)
. (5)
Підставляємо вираз (5) у вираз (3) і інтегрування:
![]() . (6)
. (6)
Ця робота йде на зміну кінетичної енергії:
![]() , (7)
, (7)
З рівнянь (1), (6) і (7) отримаємо
![]() . (8)
. (8)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (8):
=
3.89. Електрон з початковою швидкістю = З Мм/с влетів в однорідне електричне поле напруженістю Е = 150 В/м. Вектор початкової швидкості перпендикулярний лініям напруженості електричного поля. Визначити прискорення, що набуває електрон та його швидкість через 0,1 мкс.
3.89.
Дано
V0
= 3 Мм/с Е
= 150 В/м
= 0,1 мкс
=
=
= ?,
= ?
Завдяки силі Кулона, яка перпендикулярна до швидкості електрона, він рухатиметься по колу з постійною швидкістю і нормальним прискоренням, яке можна визначити із другого закону Ньютона:
![]() , (1)
, (1)
звідки
![]() . (2)
. (2)
Швидкість знаходимо згідно з формулою:
![]() . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вирази (2) і (3):
= =
3.90. Різниця потенціалів між пластинами плоского конденсатора U = 90 В. Площа кожної пластини 60 см2, її заряд 1 нКл. На якій відстані одна від одної знаходяться пластини?
3.90.
Дано
U = 90 В
= 60 см2
= 1 нКл
= ?,
Ємність плоского конденсатора дорівнює
![]() . (1)
. (1)
З визначення ємності маємо
![]() . (2)
. (2)
Для одержання відповіді, прирівняємо праві частини рівнянь (1) і (2), визначимо з цього виразу відстань між пластинами конденсатора і зробимо підстановку заданих величин у системі СІ в отриманий вираз:
![]() =
=
3.91. Площа пластин плоского повітряного конденсатора S = 0,01 м2, відстань між ними d = 5 мм. До пластин прикладена різниця потенціалів U0 = 300 В. Після відключення конденсатора від джерела напруги простір між пластинами заповнюється ебонітом. Яка різниця потенціалів при цьому встановиться між пластинами?
3.91.
Дано
S = 0,01 м2 d
= 5 мм U0
= 300 В
U = ?,
Ємність плоского
конденсатора повітряного
![]() і з заповненням ебонітом
і з заповненням ебонітом
![]() дорівнює
дорівнює
![]() . (1)
. (1)
З (1) визначаємо різницю потенціалів, яка при цьому встановиться між пластинами
![]() . (2)
. (2)
Робимо розрахунок: U =
3.92. Коаксіальний електричний кабель складається з центральної жили і концентричної циліндричної оболонки, між якими знаходиться діелектрик ε = 3,2. Знайти ємність С одиниці довжини такого кабелю, якщо радіус жили r = 1 см, а радіус оболонки R = 3,0 см.
3.92.
Дано
ε = 3,2 r
= 1 см R
= 3,0 см.
С1
= ?,
Ємність конденсатора дорівнює
![]() . (1)
. (1)
Різниця потенціалів двох точок поля дорівнює
. (2)
Модуль напруженості поля, створеного нескінченно довгого прямого рівномірно зарядженого циліндра:
. (3)
Вираз (3) підставляємо в (2) і виконуємо інтегрування:
![]() . (4)
. (4)
З (1) і (4) визначаємо ємність С1 одиниці довжини такого кабелю:
![]() . (5)
. (5)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (5):
С1 =
3.93. Знайти ємність сферичного конденсатора, що складається з двох концентричних сфер радіусами r = 10 см і R = 10,5 см. Простір між сферами заповнений маслом. Який радіус R0, повинна мати куля, занурена в масло, щоб мати таку ж ємність?
3.93.
Дано
r
= 10 см R
= 10,5 см ε
=
С1
= ?, R0
= ?
Ємність конденсатора дорівнює
. (1)
Різниця потенціалів двох точок поля дорівнює
. (2)
Модуль напруженості поля, створеного зарядженою сферою:
![]() . (3)
. (3)
Вираз (3) підставляємо в (2) і виконуємо інтегрування:
![]() . (4)
. (4)
З (1) і (4) визначаємо ємність С1:
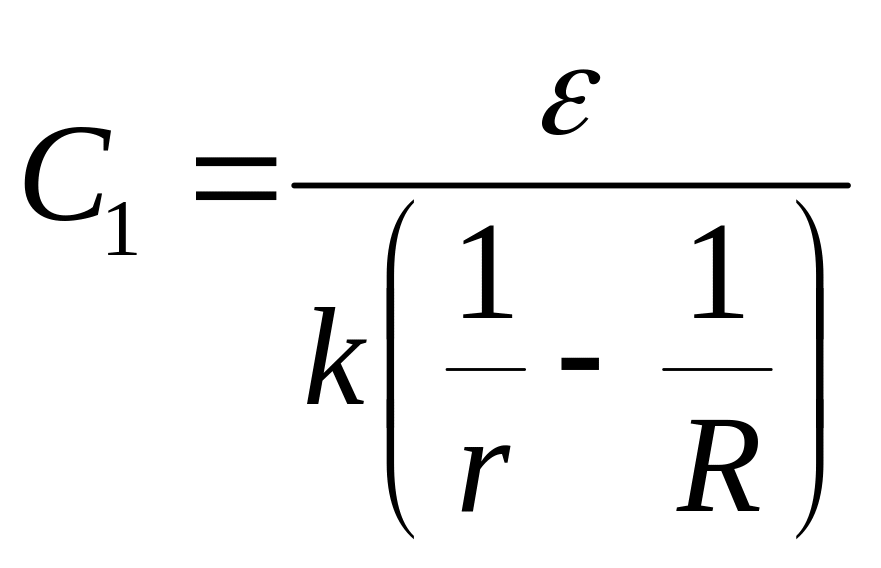 . (5)
. (5)
Куля, занурена в масло, матиме таку ємність
![]() . (6)
. (6)
З виразів (5) і (6) визначаємо радіус кулі
![]() . (7)
. (7)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вирази (5) і (7):
С1 = R0 =
3.94. Радіус внутрішньої кулі повітряного сферичного конденсатора 1 см, радіус зовнішньої кулі 4 см. Між кулями прикладена різниця потенціалів U = 3 кВ. Знайти напруженість електричного поля на відстані L = 3 см від центра меншої кулі.
3.94.
Дано
r
= 1 см R
= 4 см ε
= 1 U
= 3 кВ L
= 3 см
Е = ?
Ємність конденсатора дорівнює
![]() . (1)
. (1)
Різниця потенціалів двох точок поля дорівнює
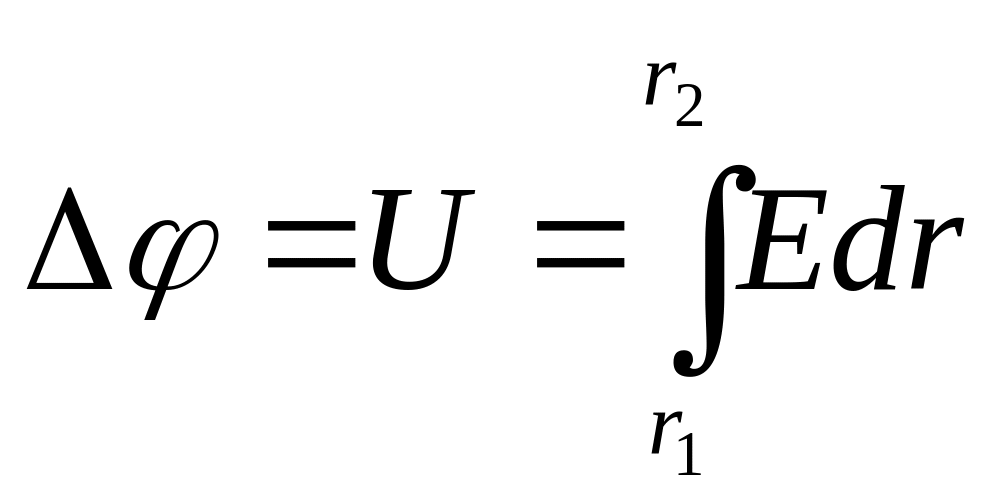 . (2)
. (2)
Модуль напруженості поля, створеного зарядженою сферою:
. (3)
Вираз (3) підставляємо в (2) і виконуємо інтегрування:
![]() . (4)
. (4)
З (1) і (4) визначаємо ємність С:
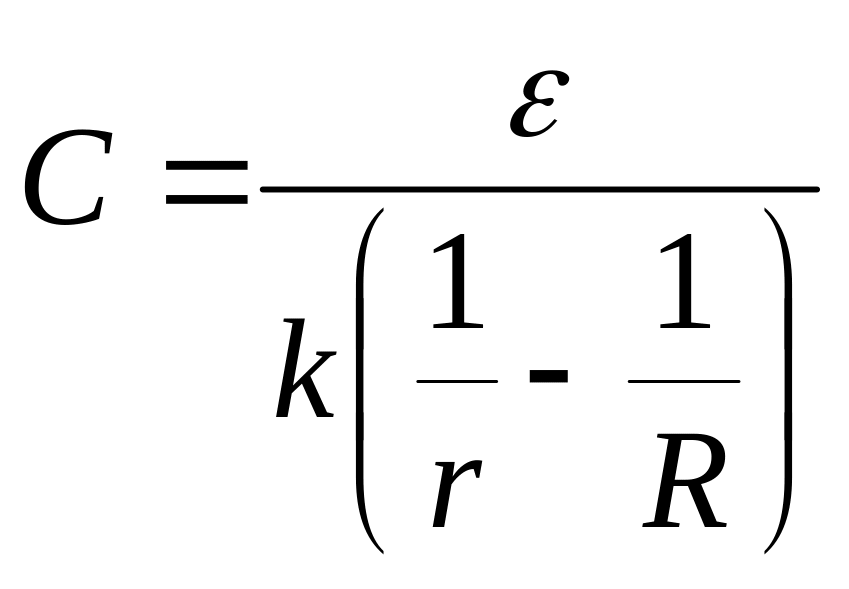 . (5)
. (5)
З формул (1) і (5) визначаємо заряд конденсатора
![]() . (6)
. (6)
Тоді з формул (3) і (5) отримаємо
![]() . (6)
. (6)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (6):
Е =
3.95. Радіус внутрішньої кулі вакуумного сферичного конденсатора 1 см, радіус зовнішньої кулі 4 см. Між кулями прикладена різниця потенціалів U = 3 кВ. Яку швидкість отримає електрон, наблизившись до центра куль з відстані 3 см до відстані 2 см?
3.95.
Дано
r
= 1 см R
= 4 см ε
= 1 U
= 3 кВ L1
= 3 см L2
= 2 см
=
=
= ?
Неоднорідне електричне поле виконує роботу по переміщенню електрона:
![]() . (1)
. (1)
Яка піде на зміну
кінетичної енергії електрона (![]() = 0 згідно з умовою задачі):
= 0 згідно з умовою задачі):
![]() . (2)
. (2)
Різниця потенціалів двох точок поля дорівнює
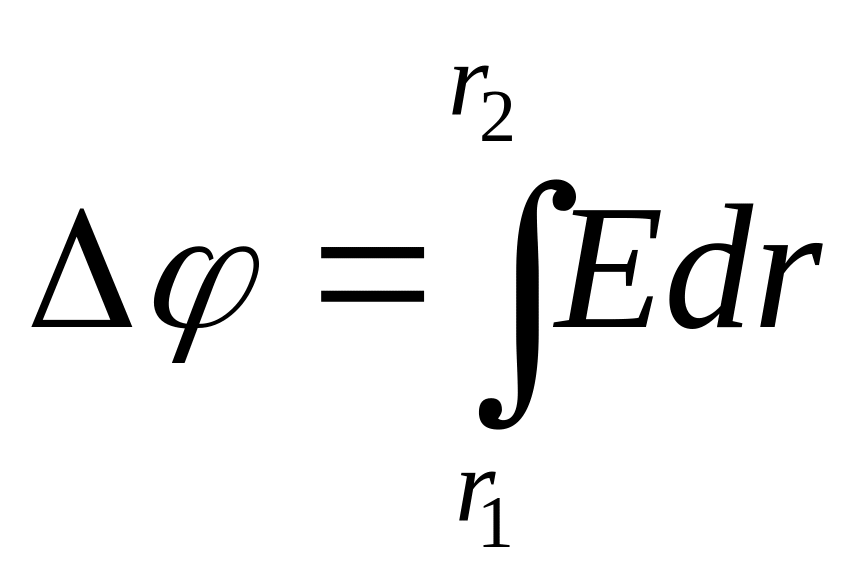 . (3)
. (3)
Модуль напруженості поля, створеного зарядом сфери:
. (4)
Вираз (4) підставляємо в (3) і виконуємо інтегрування:
![]() . (5)
. (5)
Ємність конденсатора дорівнює
. (6)
З (5) і (6) визначаємо ємність конденсатора:
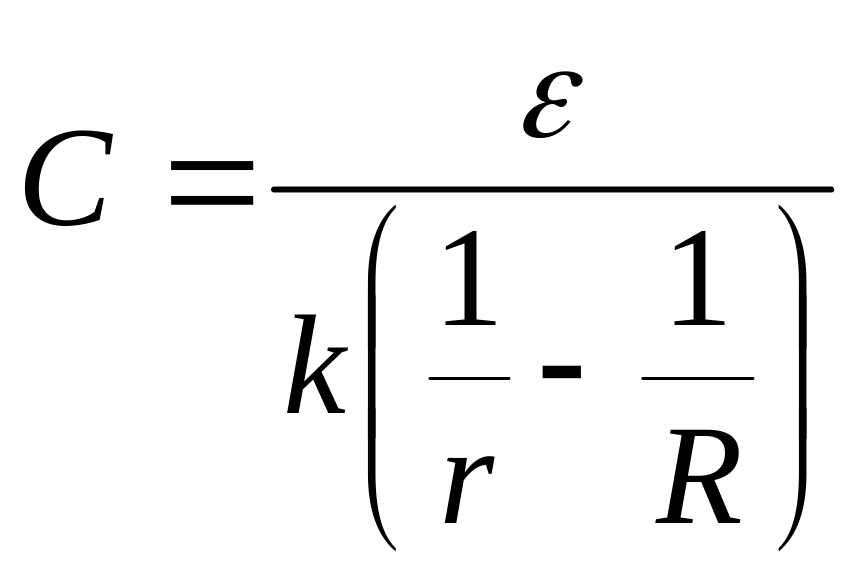 . (7)
. (7)
З формул (6) і (7) визначаємо заряд конденсатора
. (8)
Тоді з формул (5) і (8) визначаємо різницю потенціалів кінцевих точок руху електрона:
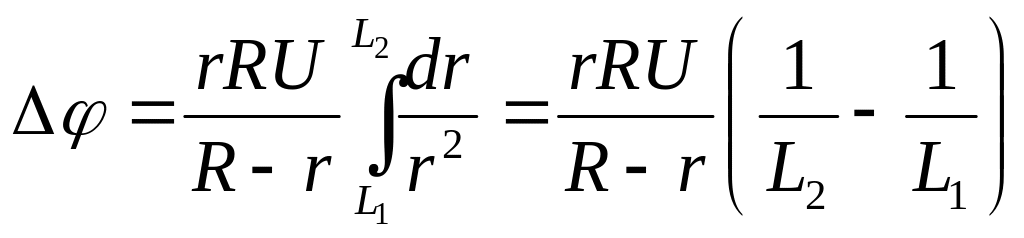 . (9)
. (9)
А з формул (1), (2) і (9) визначаємо швидкість електрона:
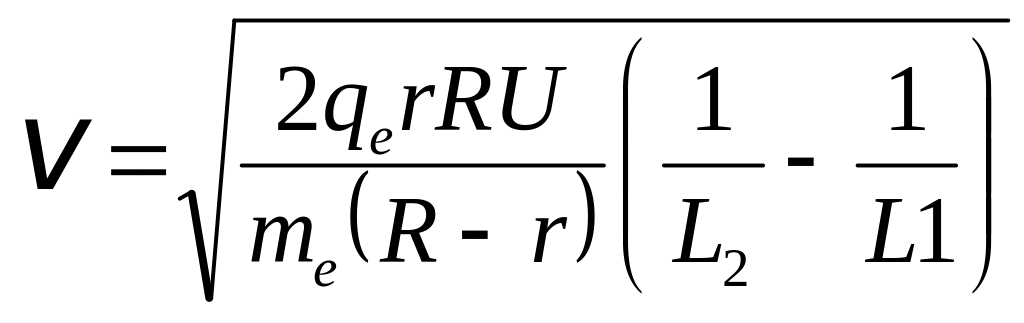 . (10)
. (10)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (10):
=
3.96. Різниця потенціалів на батареї з двох послідовно з'єднаних конденсаторів складає U = 6 В. Ємність першого конденсатора C1 = 2 мкФ, другого - С2 = 4 мкФ. Знайти заряд і різницю потенціалу на обкладках другого конденсатора.
3.96.
Дано
U = 6 В
C1
= 2 мкФ С2
= 4 мкФ
![]() = ?,
= ?,
![]() = ?
= ?
З
Рис.3.96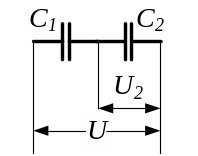
При послідовному з’єднанні конденсаторів заряд на пластинах однаковий, а ємність дорівнює
![]() . (1)
. (1)
Ємність конденсатора дорівнює
. (2)
Тоді заряд на пластинах конденсаторів дорівнює
![]() . (3)
. (3)
З формули (2) визначаємо різницю потенціалу на обкладках другого конденсатора:
![]() . (4)
. (4)
Зробимо підстановку заданих величин у системі СІ в отримані вирази (3) і (4):
= =
3.97. Заряджена куля радіусом 2 см приводиться в зіткнення з незарядженою кулею, радіусом 3 см. Після того як кулі роз'єднали, енергія другої кулі виявилася рівною W = 10 Дж. Який заряд був на першій кулі до її зіткнення з другою кулею?
3.97.
Дано
W2
= 10 Дж
![]() = 2 см
= 2 см![]() = 3 см
= 3 см
![]() = ?
= ?
Заряд, який був на першій кулі до її зіткнення з другою кулею дорівнює заряду обох куль після зіткнення:
![]() . (1)
. (1)
Заряд другої кульки визначимо з формули енергії:
![]() . (2)
. (2)
Тобто з (2) маємо
![]() . (3)
. (3)
Враховуючі, що потенціали обох куль після зіткнення будуть однаковими, то знайдемо відношення їхніх енергій:
![]() . (4)
. (4)
З останнього рівняння визначаємо енергію першої кулі після зіткнення:
![]() . (5)
. (5)
Користуючись формулою енергії зарядженої кулі (2) і виразом (5), визначимо заряд першої куль після зіткнення:
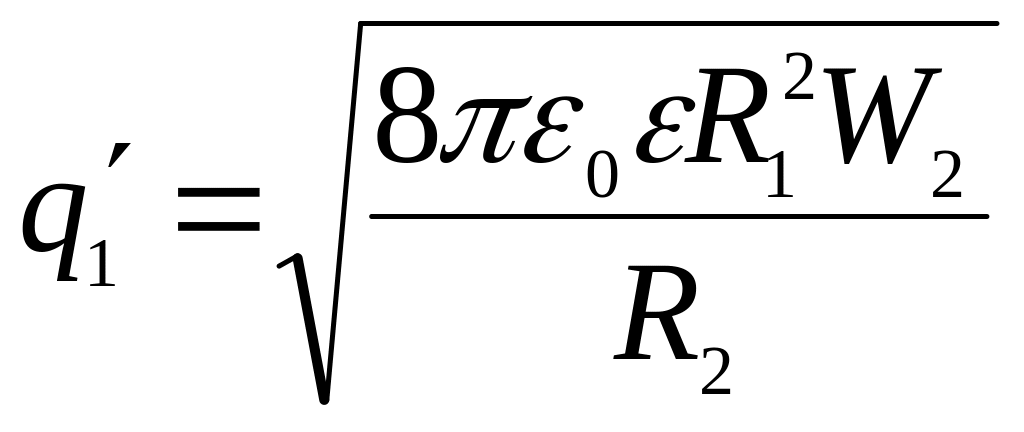 . (6)
. (6)
Для отримання відповіді, зробимо підстановку (3) і (6) у вираз (1) та підставимо задані в задачі величини у системі СІ в отриманий вираз:
=
3.98. Пластини плоского конденсатора площею S = 0,01 м2 кожна, притягуються одна до одної з силою F = 30 мН. Простір між пластинами заповнений слюдою. Знайти заряди, що знаходяться на пластинах, напруженість Е поля між пластинами і об'ємну густину енергії всередині конденсатора.
3.98.
Дано
S = 0,01 м2 F
= 30 мН ε
= 6
= ?, Е = ?,
![]() = ?
= ?
Робота при незначному зміщенні пластин конденсатора дорівнює
![]() . (1)
. (1)
Звідкіля отримаємо вираз для сили взаємодії пластин конденсатора:
![]() . (2)
. (2)
З (2) можна визначити заряд, що знаходяться на пластинах:
![]() . (3)
. (3)
Напруженість Е поля між пластинами визначаємо за формулою, користуючись виразом (3):
![]() . (4)
. (4)
Об'ємну густину енергії всередині конденсатора визначаємо за відомою формулою, та користуючись виразом (3):
![]() . (5)
. (5)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вирази (3), (4) і (5):
= Е = =
3.99. Між пластинами плоского конденсатора вкладена тонка слюдяна пластинка. Який тиск р діє на цю пластинку при напруженості електричного поля Е = 1 МВ/м?
3.99.
Дано
Е =
1 МВ/м
![]() = ?
= ?![]()
Зробимо малюнок, на якому зображена тонка слюдяна пластинка, яка розміщена між пластинами зарядженого плоского конденсатора. Вважаємо, що пластини нескінченно великі і одна з них створює електричне поле напруженістю
, (1)
де - поверхнева густина заряду на пластині; = 8,85∙10-12 Ф/м – електрична стала; - діелектрична проникність речовини ( = 1 для вакууму).
Друга пластина знаходиться в цьому полі і на неї діє сила
![]() . (2)
. (2)
Як відомо, тиск, створений силою, дорівнює:
![]() . (3)
. (3)
В вираз (3) підставляємо силу з виразу (2) і отримаємо розрахункову формулу:
= (4)
Зробимо підстановку заданих величин у системі СІ у вираз (4):
=
3.100. Площа пластин плоского повітряного конденсатора S = 0,01 м2, відстань між ними d =5 мм. Яка різниця потенціалів була прикладена до пластин конденсатора, якщо відомо, що при розряді конденсатора виділилося = 4,19 мДж теплоти?
3.100.
Дано
S = 0,01 м2 d
=5 мм
= 4,19 мДж
= ?
Вважаємо, що в тепло перетворюється вся енергія зарядженого конденсатора, тобто
![]() , (1)
, (1)
де ємність плоского конденсатора дорівнює
![]() , (2)
, (2)
= 8,85∙10-12 Ф/м – електрична стала; - діелектрична проникність речовини ( = 1 для вакууму).
З виразів (1) і (2) отримаємо розрахункову формулу:
= (3)
Зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.101.
Площа пластин
плоского повітряного конденсатора S
= 0,01 м2,
відстань між ними
![]() = 2 см. До пластин конденсатора прикладена
різниця потенціалів
= 3 кВ. Яка буде напруженість поля
конденсатора, якщо, не відключаючи його
від джерела напруги, розсунути пластини
до відстані
= 2 см. До пластин конденсатора прикладена
різниця потенціалів
= 3 кВ. Яка буде напруженість поля
конденсатора, якщо, не відключаючи його
від джерела напруги, розсунути пластини
до відстані
![]() = 5 см? Знайти енергію конденсатора після
розсунення пластин.
= 5 см? Знайти енергію конденсатора після
розсунення пластин.
3.101.
Дано
S = 0,01 м2 d1
=2 см
= 5 см
![]() =
=
![]() = 3 кВ
= 3 кВ
![]() = ?
= ?
![]() = ?
= ?
Якщо конденсатор не відключаючи від джерела напруги то можна стверджувати, що
![]() , (1)
, (1)
Електрична енергія відокремленого зарядженого провідника дорівнює
![]() . (2)
. (2)
Для плоского конденсатора
![]() , (3)
, (3)
де
![]() — об'єм,
обмежений пластинами конденсатора.
— об'єм,
обмежений пластинами конденсатора.
Тоді після розсунення пластин конденсатора будемо мати
![]() , (3)
, (3)
= 8,85∙10-12 Ф/м – електрична стала; - діелектрична проникність речовини ( = 1 для вакууму).
Зробимо підстановку заданих величин у системі СІ у вирази (1) і (3) та отримаємо відповіді:
= =
3.102. Розв'язати попередню задачу при умові, що спочатку конденсатор відключається від джерела напруги, а потім розсовуються пластини конденсатора.
3.102.
Дано
S = 0,01 м2 d1
=2 см
= 3 кВ
= 5 см
= ?
= ?
![]()
Якщо конденсатор відключити від джерела напруги то можна стверджувати, що
![]() . (1)
. (1)
Ємність плоского конденсатора дорівнює
![]() , (2)
, (2)
де = 8,85∙10-12 Ф/м – електрична стала; - діелектрична проникність речовини ( = 1 для вакууму).
Підставляємо ємності конденсаторів з виразу (2) у формулу (1) і отримаємо
![]() . (3)
. (3)
Електрична енергія відокремленого зарядженого провідника дорівнює
. (4)
Для плоского конденсатора
, (5)
де — об'єм, обмежений пластинами конденсатора.
Тоді після розсунення пластин конденсатора будемо мати
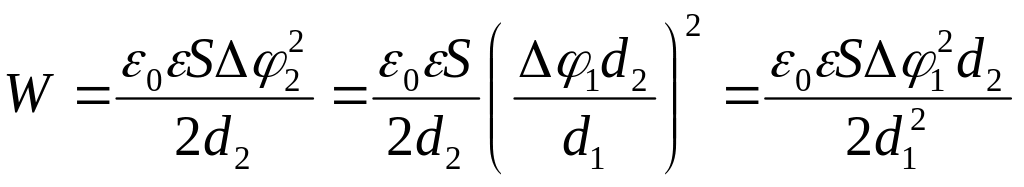 , (6)
, (6)
= 8,85∙10-12 Ф/м – електрична стала; - діелектрична проникність речовини ( = 1 для вакууму).
Зробимо підстановку заданих в умові величин у системі СІ у вирази (3) і (6) та отримаємо відповіді:
= =
3.103.
Плоский
конденсатор заповнений діелектриком
і на його пластини подана деяка різниця
потенціалів. Його енергія при цьому
складає
![]() = 20 мкДж. Після того, як конденсатор
відключили від джерела живлення,
діелектрик вийняли з конденсатора.
Робота, яку треба було здійснити, щоб
вийняти діелектрик склала
= 70 мкДж. Знайти діелектричну проникність
ε діелектрика.
= 20 мкДж. Після того, як конденсатор
відключили від джерела живлення,
діелектрик вийняли з конденсатора.
Робота, яку треба було здійснити, щоб
вийняти діелектрик склала
= 70 мкДж. Знайти діелектричну проникність
ε діелектрика.
3.103.
Дано
= 20 мкДж
= 70 мкДж
= ?
Робота, яку треба здійснити, щоб вийняти діелектрик з конденсатора, дорівнює зміні його енергії:
![]() . (1)
. (1)
Ємність плоского конденсатора дорівнює
![]() , (2)
, (2)
де = 8,85∙10-12 Ф/м – електрична стала; - діелектрична проникність речовини ( = 1 для вакууму).
Для плоского конденсатора енергія електричного поля дорівнює
![]() . (3)
. (3)
Тоді для двох конденсаторів, з урахуванням виразу (2), будемо мати
![]() , (4)
, (4)
де - діелектрична проникність речовини ( = 1 для вакууму).
Підставляємо енергію з виразів (4) у формулу (1) і отримаємо:
![]() . (5)
. (5)
Звідки можна получити вираз для розрахунку діелектричної проникності ε діелектрика:
![]() = (6)
= (6)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (6) та отримаємо відповідь:
=
3.104. Простір між пластинами плоского конденсатора заповнений діелектриком, діелектрична сприйнятливість якого χ = 0,08. Відстань між пластинами = 5 мм. На пластини конденсатора подана різниця потенціалів = 4 кВ. Знайти поверхневу густина зв'язаних зарядів на діелектрику.
3.104.
Дано
χ = 0,08
= 5 мм
= 4 кВ
![]() = ?
= ?
Д
Рис. 3.104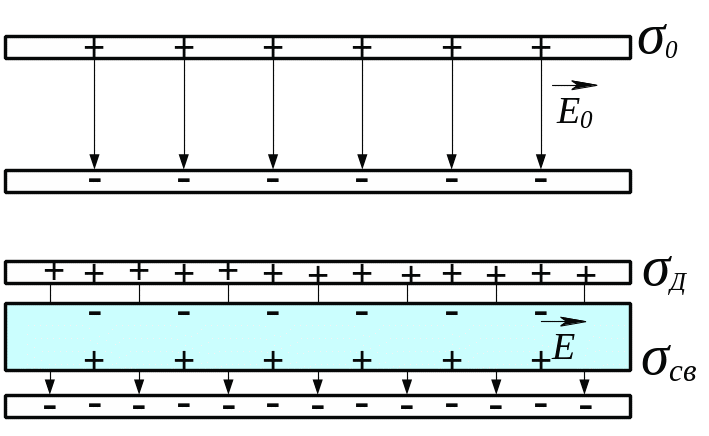
![]() . (1)
. (1)
Позначимо через
![]() ,
,
![]() - поверхневу густину заряду на пластинах
конденсатора в відсутності діелектрика,
в присутності діелектрика;
- поверхневу густину заряду на пластинах
конденсатора в відсутності діелектрика,
в присутності діелектрика;
![]() - поверхневу густину зв’язаних
(поляризованих) зарядів.
- поверхневу густину зв’язаних
(поляризованих) зарядів.
Спільна дія зарядів густиною і така, якби на межі провідник – діелектрик існує заряд, розподілений з густиною
![]() . (2)
. (2)
Таким чином,
![]() - поверхнева густина «ефективних»
зарядів, які визначають сумарне,
результуюче поле в діелектрику.
- поверхнева густина «ефективних»
зарядів, які визначають сумарне,
результуюче поле в діелектрику.
Як відомо, поверхнева густина заряду пов’язана з відповідними полями такими співвідношеннями:
поле в відсутності діелектрика
![]() ; (3)
; (3)
результуюче поле в діелектрику
![]() . (4)
. (4)
З виразів (2) та (4) отримуємо
![]() . (5)
. (5)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (5) та отримаємо відповідь:
=
3.105. Простір між пластинами плоского конденсатора заповнений склом. Площа пластин конденсатора S = 0,01 м2. Пластини конденсатора притягуються одна до одної з силою F = 4,9 мН. Знайти поверхневу густина зв'язаних зарядів на склі.
Рис. 3.105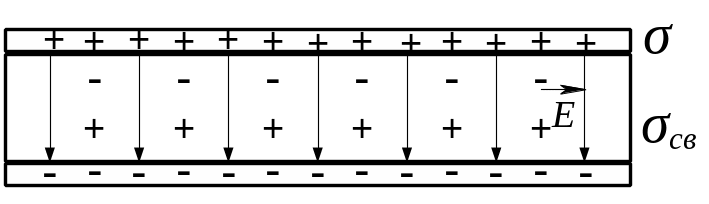
3.105.
Дано
= 6 S
= 0,01 м2 F
= 4,9 мН
= ?
Сила притягання пластин плоского конденсатора: а) конденсатор від’єднали від джерела струму; б) приєднаний до джерела струму;
а)
![]() . (1)
. (1)
б)
![]() . (2)
. (2)
Вважаємо, що маємо справу з першим випадком, тобто конденсатор від’єднали від джерела струму. Тоді маємо
![]() . (3)
. (3)
Позначимо через , - поверхневу густину заряду на пластинах конденсатора в відсутності діелектрика, в присутності діелектрика; - поверхневу густину зв’язаних (поляризованих) зарядів.
Спільна дія зарядів густиною і така, якби на межі провідник – діелектрик існує заряд, розподілений з густиною
. (4)
Таким чином, - поверхнева густина «ефективних» зарядів, які визначають сумарне, результуюче поле в діелектрику.
Як відомо, поверхнева густина заряду пов’язана з відповідними полями такими співвідношеннями:
поле в відсутності діелектрика
![]() ; (5)
; (5)
результуюче поле в діелектрику
![]() . (6)
. (6)
З виразів (4) та (6) отримуємо
![]() . (7)
. (7)
Підставляємо в вираз (7) значення напруженості поля з (6) та густини заряду з виразу (3) і отримаємо вираз для розрахунку відповіді:
![]() . (7)
. (7)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (7) та отримаємо відповідь:
=
3.106.
До батареї
з е.р.с у
![]() = 300 В включені два плоских конденсатори
ємностями С1
= 2 пФ і С2
= 3 пФ. Визначити заряд Q
і напругу U
на конденсаторах при їх послідовному
з'єднанні.
= 300 В включені два плоских конденсатори
ємностями С1
= 2 пФ і С2
= 3 пФ. Визначити заряд Q
і напругу U
на конденсаторах при їх послідовному
з'єднанні.
3.106.
Дано
= 300 В С1
= 2 пФ С2
= 3 пФ
Q = ? U1
= ? U2
= ?
Рис. 3.106
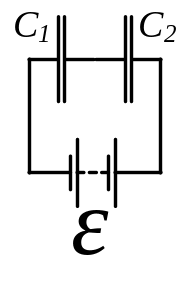
При паралельному з'єднанні конденсаторів ємність батареї дорівнює
![]() , (1)
, (1)
при послідовному з'єднанні
![]() . (2)
. (2)
Тобто електрична ємність заданої батареї конденсаторів визначається за формулою:
![]() . (3)
. (3)
Для кожного відокремленого провідника відношення заряду до потенціалу провідника є величина стала
![]() , (4)
, (4)
де — електрична ємність батареї конденсаторів.
Напругу U на конденсаторах визначаємо за формулами:
![]() (5)
(5)
Зробимо підстановку заданих в умові величин у системі СІ у вирази (4) і (5) та отримаємо відповіді:
Q = U1 = U2 =
3.107. До батареї з е.р.с у = 300 В включені два плоских конденсатори ємностями С1 = 2 пФ і С2 = 3 пф. Визначити заряд Q і напругу U на конденсаторах при їх паралельному з'єднанні.
3.107.
Дано
= 300 В С1
= 2 пФ С2
= 3 пФ
Q1
= ? U = ? Q2
= ?
Рис. 3.107
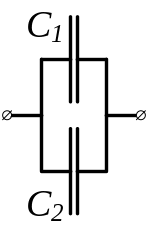
При паралельному з'єднанні конденсаторів ємність батареї дорівнює
, (1)
при послідовному з'єднанні
. (2)
Тобто електрична ємність заданої батареї конденсаторів визначається за формулою:
![]() . (3)
. (3)
Загальний заряд на батареї конденсаторів можна знайти за формулою
![]() , (4)
, (4)
де — електрична ємність батареї конденсаторів.
Заряд на конденсаторах визначаємо за формулами, а перевірку можна виконати за формулою (4):
![]() (5)
(5)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (5) та отримаємо відповіді:
Q1 = Q2 = U = = 300 В
3.108. Конденсатор ємністю С1 = 600 пФ зарядили до різниці потенціалів U1 = 1,5 кВ і відключили від джерела напруги, Потім до нього паралельно приєднали незаряджений конденсатор ємністю С2 = 400 пФ. Визначити енергію, витрачену на утворення іскри, що проскочила при з'єднанні конденсаторів.
3.108.
Дано
U1
= 1,5 кВ С1
= 600 пФ С2
= 400 пФ
Рис. 3.108
![]() = ?
= ?
При паралельному з'єднанні конденсаторів ємність батареї дорівнює
, (1)
при послідовному з'єднанні
. (2)
Тобто електрична ємність заданої батареї конденсаторів визначається за формулою:
. (3)
Загальний заряд на батареї конденсаторів дорівнюватиме заряду на першому конденсаторі
![]() . (4)
. (4)
Визначаємо енергію, витрачену на утворення іскри, що проскочила при з'єднанні конденсаторів з закону збереження енергії:
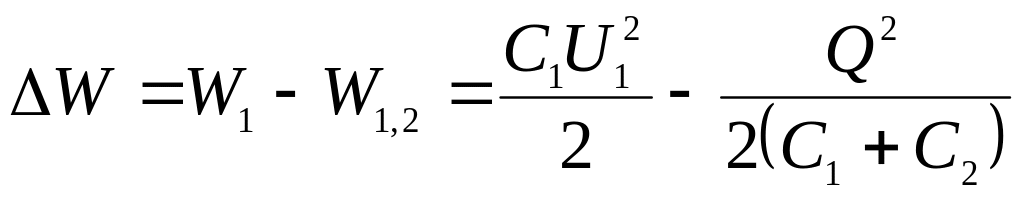 , (5)
, (5)
де
![]() - енергія електричного поля в першому
конденсаторі і в паралельному з’єднанні
конденсаторів.
- енергія електричного поля в першому
конденсаторі і в паралельному з’єднанні
конденсаторів.
Підставляємо заряд з виразу (4) у формулу (5) і отримаємо вираз для розрахунку відповіді:
= (6)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (6) та отримаємо відповідь:
=
3.109. Конденсатори ємністю С1 = 5 мкФ і С2 = 10 мкФ заряджені до напруги U1 = 60 В и U2 = 100 В, відповідно. Визначити напругу на обкладках конденсаторів після їхнього з'єднання обкладками, що мають однойменні заряди.
3.109.
Дано
U1
= 60 В U2
= 100 В С1
= 5 мкФ С2
= 10 мкФ
= ?
Рис. 3.109
Згідно закону збереження кількості заряду можна стверджувати, що заряд на батареї конденсаторів дорівнює сумі зарядів на кожному з них
![]() . (1)
. (1)
Визначити напругу на обкладках конденсаторів після їхнього з'єднання обкладками, що мають однойменні заряди, можна за формулою
![]() . (2)
. (2)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (2) та отримаємо відповідь:
=
3.110. Конденсатор ємністю С1 = 10 мкФ заряджений до напруги U = 10 В. Визначити заряд на обкладках цього конденсатора після того, як паралельно йому був підключений інший, незаряджений, конденсатор ємністю С2 = 20 мкФ.
3.110.
Дано
U1
= 10 В U2
= 0 С1
= 10 мкФ С2
= 20 мкФ
Рис. 3.110
![]() = ?
= ?
Згідно закону збереження кількості заряду можна стверджувати, що заряд на першому конденсаторі дорівнюватиме сумі зарядів на кожному з них після з’єднання
![]() . (1)
. (1)
Визначити напругу на обкладках конденсаторів після їхнього з'єднання обкладками, що мають однойменні заряди, можна за формулою
![]() . (2)
. (2)
Тоді заряд на першому конденсаторі після з’єднання його з другим дорівнюватиме
![]() . (3)
. (3)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (3) та отримаємо відповідь:
=
3.111. Конденсатори ємностями С1 = 2 мкФ, С2 = 5 мкФ і С3 = 10 мкФ з'єднані послідовно і знаходяться під напругою U = 850 В. Визначити напругу і заряд на першому з конденсаторів.
3.111.
Дано
U
= 850 В С1
= 2 мкФ С2
= 5 мкФ С3
= 10 мкФ
= ?
Рис. 3.111
![]() = ?
= ?
При послідовному з’єднанні конденсаторів заряд на кожному з них буде однаковий
![]() , (1)
, (1)
де при послідовному з'єднанні загальна ємність дорівнює
![]() . (2)
. (2)
Підставляємо загальну ємність з виразу (2) у формулу (1) і отримаємо заряд на першому конденсаторі:
![]() . (3)
. (3)
Напруга на першому конденсаторі визначаємо за формулою:
![]() . (4)
. (4)
Заряд з виразу (3) підставляємо у формулу (4) і отримаємо вираз для розрахунку напруги:
= (5)
Зробимо підстановку заданих в умові величин у системі СІ у вирази (3) та (5) і отримаємо відповідь:
= =
3.112. Два конденсатори ємностями С1 = 2 мкФ і С2 = 5 мкФ заряджені до напруги U1 = 100 В та U2 = 150 В, відповідно. Визначити напругу на обкладках конденсаторів після їхнього з'єднання обкладками, що мають різнойменні заряди.
3.112.
Дано
U1
= 100 В U2
= 150 В С1
= 2 мкФ С2
= 5 мкФ
= ?
Рис. 3.112
Після з'єднання конденсаторів обкладками, що мають різнойменні заряди, частина зарядів нейтралізується і на батареї залишиться заряд:
![]() . (1)
. (1)
Тоді напруга на обкладках конденсаторів після їхнього з'єднання обкладками, що мають різнойменні заряди, дорівнюватиме
![]() . (2)
. (2)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (2) та отримаємо відповідь:
=
3.113. Два однакових плоских повітряних конденсатори ємністю 100 пФ кожний з'єднані в батарею послідовно. Визначити, на скільки зміниться ємність цієї батареї, якщо простір між пластинами одного з конденсаторів заповнити парафіном.
3.113.
Дано
С1
= С2
= 100 пФ
= 2
![]() = ?
= ?
Зміну електричної ємності батареї, якщо простір між пластинами одного з конденсаторів, наприклад, другого, заповнити парафіном визначаємо за формулою:
![]() , (1)
, (1)
де
![]() ,
,
![]() - ємності батарей конденсаторів до і
після заповнення парафіном простору
між пластинами другого конденсатора.
- ємності батарей конденсаторів до і
після заповнення парафіном простору
між пластинами другого конденсатора.
При послідовному з'єднанні загальна ємність дорівнює
![]() . (2)
. (2)
Запишемо вирази ємностей отриманих батарей конденсаторів:
![]() (3)
(3)
Підставляємо загальні ємності з виразу (3) у формулу (1) і отримаємо вираз для розрахунку зміни ємності цієї батареї:
= . (4)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (4) і отримаємо відповідь:
=
3.114. Два конденсатори ємностями С1 = 5 мкФ і С2 = 8 мкФ з'єднані послідовно і приєднані до батареї з е.р.с. у = 80 В. Визначити заряд та різницю потенціалів на першому з конденсаторів.
3.114.
Дано
= 80 В С1
= 5 мкФ С2
= 8 мкФ
= ?
= ?
Рис. 3.114
При послідовному з’єднанні конденсаторів заряд на кожному з них буде однаковий
![]() , (1)
, (1)
де при послідовному з'єднанні загальна ємність дорівнює
. (2)
Підставляємо загальну ємність з виразу (2) у формулу (1) і отримаємо заряд на першому конденсаторі:
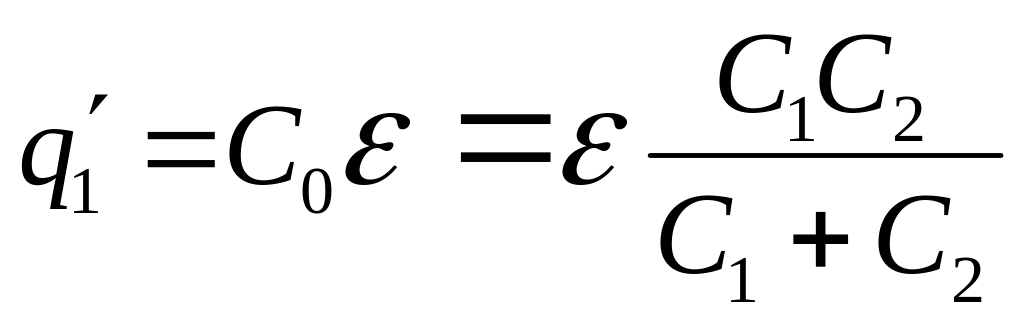 . (3)
. (3)
Напруга на першому конденсаторі визначаємо за формулою:
. (4)
Заряд з виразу (3) підставляємо у формулу (4) і отримаємо вираз для розрахунку напруги:
= (5)
Зробимо підстановку заданих в умові величин у системі СІ у вирази (3) та (5) і отримаємо відповідь:
= =
3.115. Плоский конденсатор складається з двох круглих пластин радіусом R = 10 см кожна. Відстань між пластинами = 2 мм. Конденсатор приєднаний до джерела напруги = 80 В. Визначити заряд Q та напруженість Е поля всередині конденсатора, коли він заповнений склом.
3.115.
Дано
R
= 10 см
= 80 В
= 2 мм
= 6
Q = ? Е
= ?
Ємність плоского конденсатора:
![]() (1)
(1)
де
=
![]() — площа кожної пластини;
- відстань між пластинами.
— площа кожної пластини;
- відстань між пластинами.
Для кожного відокремленого провідника відношення заряду до потенціалу провідника є величина стала
![]() , (2)
, (2)
де — електрична ємність провідника.
З формул (2) та (1) отримуємо заряд конденсатора
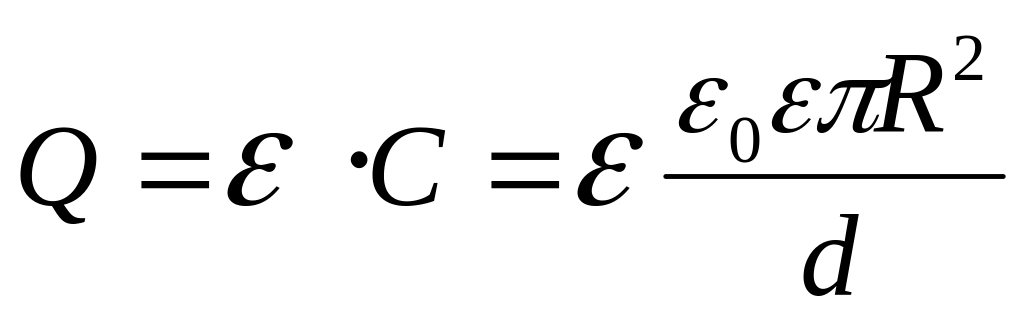 , (3)
, (3)
Для однорідного поля (поля плоского конденсатора) напруженість дорівнює
![]() ,
(4)
,
(4)
де — різниця потенціалів між пластинами конденсатора; d — відстань між ними.
Зробимо підстановку заданих в умові величин у системі СІ у вирази (3) та (4) і отримаємо відповідь:
Q = Е =
3.116. Дві металеві кульки радіусами R1 = 5 см і R2 = 10 см мають заряди Q1 = 40 нКл і Q2 = - 20 нКл, відповідно. Знайти енергію W яка виділиться при з'єднанні куль провідником.
3.116.
Дано
R1
= 5 см R2
= 10 см Q1
= 40 нКл Q2
= - 20 нКл
= ?
Енергію W яка виділиться при з'єднанні куль провідником дорівнюватиме різниці енергій куль до і після з’єднання їх провідником:
![]() . (1)
. (1)
Електрична енергія відокремленого зарядженого провідника
. (2)
Ємність провідної кулі радіуса г
![]() . (3)
. (3)
Тоді енергія куль до з’єднання дорівнює
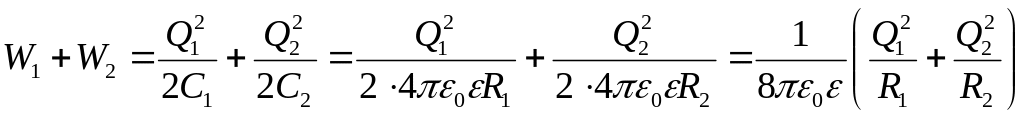 . (4)
. (4)
При з’єднанні куль провідником заряди будуть переміщатися доки потенціали куль не зрівняються, тоді нові заряди куль можна визначити за формулами:
![]() . (5)
. (5)
А сумарний заряд куль після з’єднання дорівнюватиме
![]() . (6)
. (6)
З рівнянь (5) та (6) можна визначити заряди куль після їхнього з’єднання:
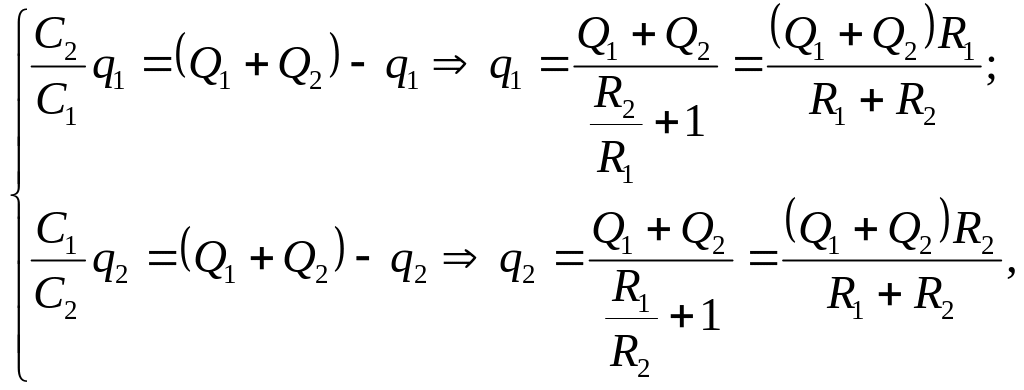 (7)
(7)
тоді енергія електричного поля куль після їхнього з’єднання дорівнюватиме
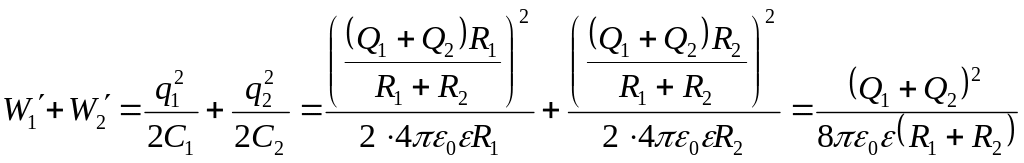 . (8)
. (8)
Енергії з виразів (4) та (8) підставляємо в формулу (1) і отримаємо вираз для розрахунку відповіді:
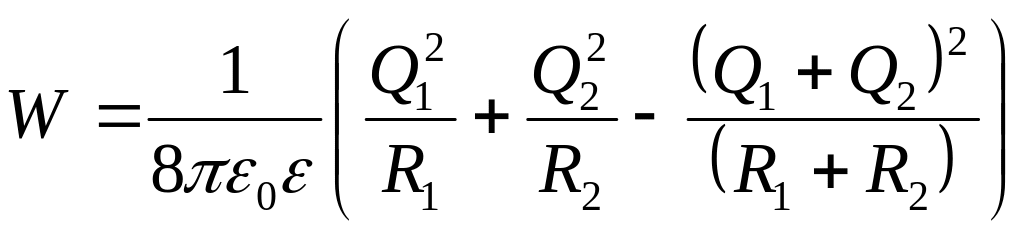 . (8)
. (8)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (8) і отримаємо відповідь:
=
3.117. Простір між
пластинами плоского конденсатора
заповнено двома шарами діелектрика:
скла (![]() = 6) товщиною d1
= 0,2 см і шаром парафіну (
= 6) товщиною d1
= 0,2 см і шаром парафіну (![]() = 2) товщиною d2
= 0,3 см. Різниця потенціалів між обкладками
= 300 В. Визначити напруженість Е
поля і падіння потенціалу в кожному із
шарів.
= 2) товщиною d2
= 0,3 см. Різниця потенціалів між обкладками
= 300 В. Визначити напруженість Е
поля і падіння потенціалу в кожному із
шарів.
3.117.
Дано
d1
= 0,2 см
= 6 d2
= 0,3 см
= 2
= 300 В
![]() = ?
= ?
![]() = ?
= ?![]() = ?
= ?
![]() = ?
= ?
Щоб знайти величини
![]() ,
,
![]() ,
з'ясуємо зв'язок, що існує між ними і
різницею потенціалів
.
Скористаємося формулою зв’язку
між потенціалом і напруженістю поля.
Тобто градієнт потенціалу
дорівнює
напруженості поля
,
з'ясуємо зв'язок, що існує між ними і
різницею потенціалів
.
Скористаємося формулою зв’язку
між потенціалом і напруженістю поля.
Тобто градієнт потенціалу
дорівнює
напруженості поля
![]() .
(1)
.
(1)
Зв’язок між напруженістю та потенціалом поля:
. (2)
Звідки різниця потенціалів двох точок поля дорівнює
. (3)
Для однорідного поля (поля плоского конденсатора) напруженість
![]() ,
(4)
,
(4)
де U — різниця потенціалів між пластинами конденсатора; d — відстань між ними.
Розбивши весь шлях інтегрування на дві частини, які відповідні товщині двох шарів діелектриків (товщиною зазору нехтуємо), і враховуючи, що в межах кожного шару поле однорідне, отримаємо
![]() .
(5)
.
(5)
Так як електричний
зсув
![]() в обох шарах діелектриків має одне і те
ж значення, то скорочуючи на
запишемо:
в обох шарах діелектриків має одне і те
ж значення, то скорочуючи на
запишемо:
![]() .
(6)
.
(6)
Вирішуючи спільно рівняння (5) і (6), одержимо:
![]() ;
;
![]() . (7)
. (7)
З формули (5) можна отримати падіння потенціалу в кожному із шарів:
![]() .
(8)
.
(8)
Зробимо підстановку заданих в умові величин у системі СІ у вирази (7) та (8) і отримаємо відповіді:
= = = =
` 3.118. Плоский конденсатор з площею пластин S = 200 см2 кожна, заряджений до різниці потенціалів = 2 кВ. Відстань між пластинами d = 2 см. Діелектрик – скло ( = 6). Визначити енергію W конденсатора та її густину ω.
3.118.
Дано
S
= 200 см2
= 2 кВ
= 2 см
= 6
W = ? ω
= ?
Електрична енергія відокремленого зарядженого провідника ємністю і потенціалом дорівнює
![]() . (1)
. (1)
Для плоского конденсатора електрична ємність дорівнює
(2)
тоді енергію можна визначити за формулами:
![]() , (3)
, (3)
Об'ємна густина енергії електричного поля
![]() , (4)
, (4)
де
![]() - електричне зміщення, Кл/м2.
— об'єм,
обмежений пластинами конденсатора.
- електричне зміщення, Кл/м2.
— об'єм,
обмежений пластинами конденсатора.
Зробимо підстановку заданих в умові величин у системі СІ у вирази (3) та (4) і отримаємо відповіді:
W = ω =
3.119. Конденсатори ємністю С1 = 5 мкФ і С2 = 10 мкФ заряджені до напруги U1 = 60 В и U2 = 100 В, відповідно. Визначити напругу на обкладках конденсаторів після їхнього з'єднання обкладками; що мають однойменні заряди.
3.119.
Дано
U1
= 60 В U2
= 100 В С1
= 5 мкФ С2
= 10 мкФ
= ?
Рис. 3.119
Згідно закону збереження кількості заряду можна стверджувати, що заряд на батареї конденсаторів дорівнює сумі зарядів на кожному з них
. (1)
Визначити напругу на обкладках конденсаторів після їхнього з'єднання обкладками, що мають однойменні заряди, можна за формулою
. (2)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (2) та отримаємо відповідь:
=
3.120. Скільки витків ніхромового дроту діаметром = 1 мм треба навити на фарфоровий циліндр радіусом = 2,5 см, щоб отримати опір у = 40 Ом?
3.120.
Дано
= 1 мм
= 2,5 см
= 40 Ом
= ?
Кількість витків визначимо як відношення довжин дроту та одного витка:
![]() . (1)
. (1)
Опір циліндричного провідника довжиною та площею поперечного перерізу
![]() , (2)
, (2)
де
![]() — питомий опір.
— питомий опір.
Довжину дроту визначаємо з формули (2) та підставляємо у (1) і получаємо вираз для розрахунку кількості витків:
= (3)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (3) та отримаємо відповідь:
=
3.121. Резистор з опором R1 = 5 Ом, вольтметр і джерело струму з'єднані паралельно. Вольтметр показує напруга U1 = 10 В. Якщо замінити резистор іншим з опором R2 = 12 Ом, то вольтметр покаже напруга U2 = 12 В: Визначити е.р.с. і внутрішній опір джерела струму.
3.121.
Рис. 3.121
Дано
R1
= 5 Ом
U1
= 10 В R2
= 120 Ом U2
= 12 В
= ?
= ?
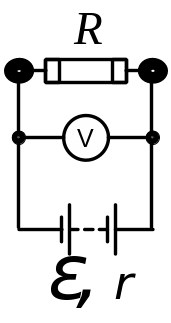
Закон Ома для повного електричного кола має вигляд:
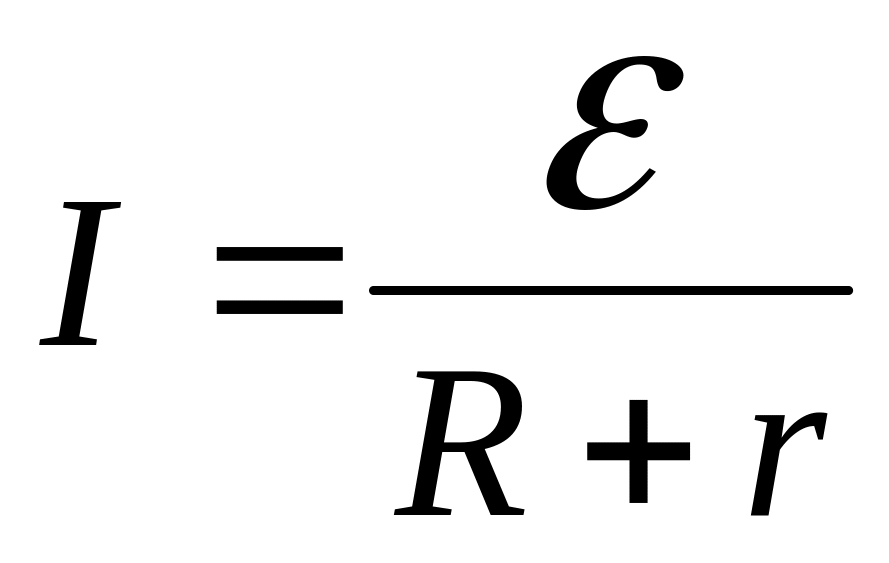 , (1)
, (1)
де — зовнішній опір; — внутрішній опір кола.
Запишемо формулу цього закону для двох випадків підключення опорів:
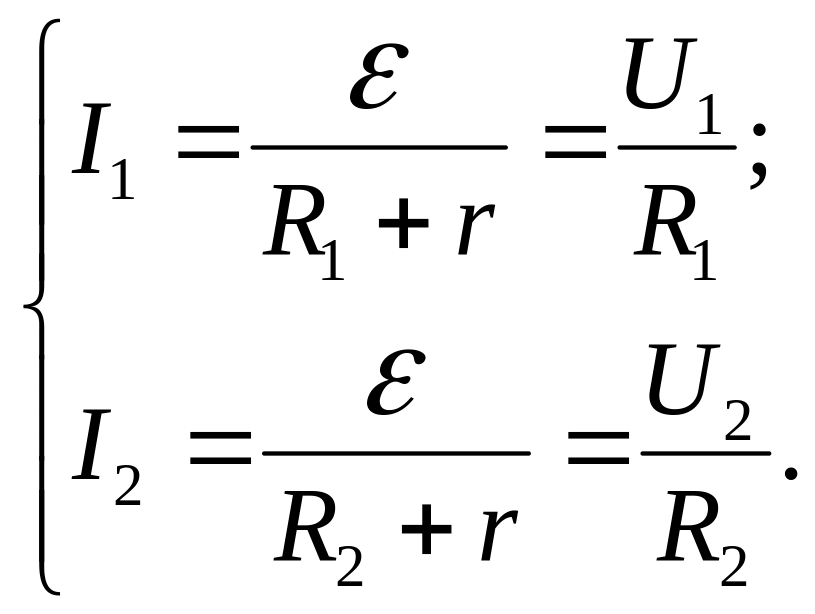 . (2)
. (2)
Знаходимо відношення першого рівняння системи (2) до другого і отримаємо вираз для розрахунку внутрішнього опору джерела струму:
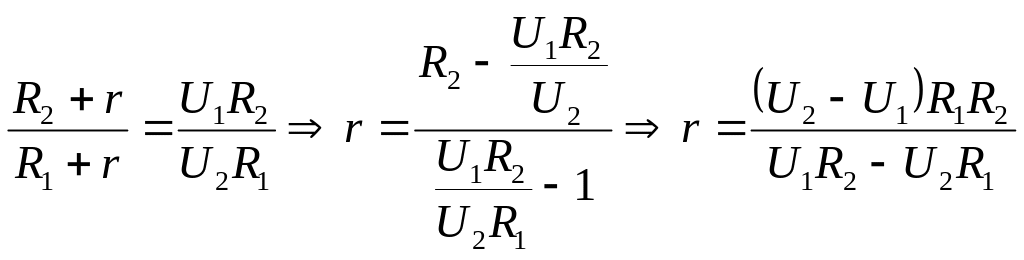 , (3)
, (3)
З любого рівняння системи (3), наприклад, другого, визначаємо електрорушійну силу джерела струму і підставляємо в одержану формулу значення внутрішнього опору джерела струму :
![]() = (4)
= (4)
Зробимо підстановку заданих в умові величин у системі СІ у вирази (3) та (4) отримаємо відповіді:
= =
3.122. Визначити електричний заряд, що пройшов за = 20 секунд крізь поперечний переріз проводу з опором R = 3 Ом при рівномірному наростанні напруги на його кінцях від U1 = 2 В до U2 = 4 В.
3.122.
Дано
= 20 с
R
= 3 Ом U1
= 2 В U2
= 4 В
= ?
С
Рис. 3.122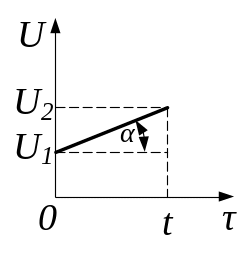
![]() . (1)
. (1)
Звідки можна отримати вираз для визначення електричного заряду, що проходить через перетин провідника за заданий час:
![]() . (2)
. (2)
Для визначення рівняння зміни напруги на кінцях проводу, побудуємо графік цієї залежності (див рис. 3.122):
![]() . (2)
. (2)
Підставляємо рівняння напруги з (2) під знак інтеграла
. (3)
 . (4)
. (4)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (4) та отримаємо відповідь:
=
3.123. Визначити силу
струму в електричному колі, що складається
з двох джерел живлення з'єднаних
однойменними полюсами, з е.р.с.
![]() = 1,6 В та
= 1,6 В та
![]() = 1,2 В. їх внутрішній опір r1
= 0,6 Ом, r2
= 0,4 Ом.
= 1,2 В. їх внутрішній опір r1
= 0,6 Ом, r2
= 0,4 Ом.
3.123.
Дано
= 1,6 В
= 1,2 В r1
= 0,6 Ом r2
= 0,4 Ом
Рис. 3.123
![]() = ?
= ?
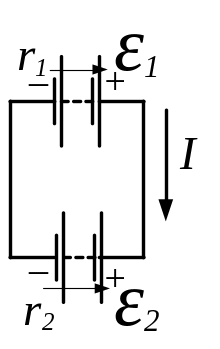
Зробимо малюнок, на який наносимо напрямок току та електрорушійної сили в кожному джерелі струму. Вибираємо обхід контуру проти годинникової стрілки і записуємо формулу другого закону Кірхгофа:
![]() . (1)
. (1)
З рівняння (1) отримаємо вираз для розрахунку силу струму в електричному колі:
= (2)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.124. Гальванічний
елемент дає на зовнішній опір у
![]() = 0,5 Ом силу струму
= 0,5 Ом силу струму
![]() = 0,2 А. Якщо зовнішній опір замінити на
R2
= 0,8 Ом, то елемент дає силу струму І2
= 0,15 А. Визначити силу струму короткого
замикання.
= 0,2 А. Якщо зовнішній опір замінити на
R2
= 0,8 Ом, то елемент дає силу струму І2
= 0,15 А. Визначити силу струму короткого
замикання.
3.124.
Рис. 3.124
Дано
= 0,5 Ом
= 0,2 А R2
= 0,8 Ом І2
= 0,15 А
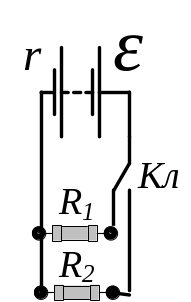
![]() = ?
= ?
Зробимо малюнок.
Закон Ома для повного кола має вигляд:
, (1)
де — зовнішній опір; — внутрішній опір.
З рівняння (1) можна зробити висновок, що струм короткого замикання отримаємо, якщо зовнішній опір кола дорівнюватиме нулю:
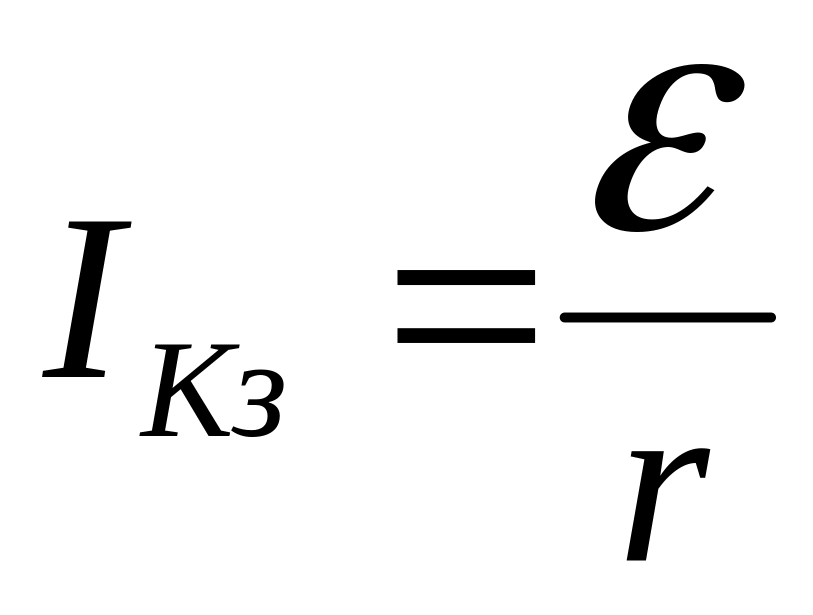 , (2)
, (2)
Для визначення параметрів джерела струму: електрорушійної сили і внутрішнього опору, складемо систему рівнянь з формули закону Ома для двох випадків підключення зовнішнього опору:
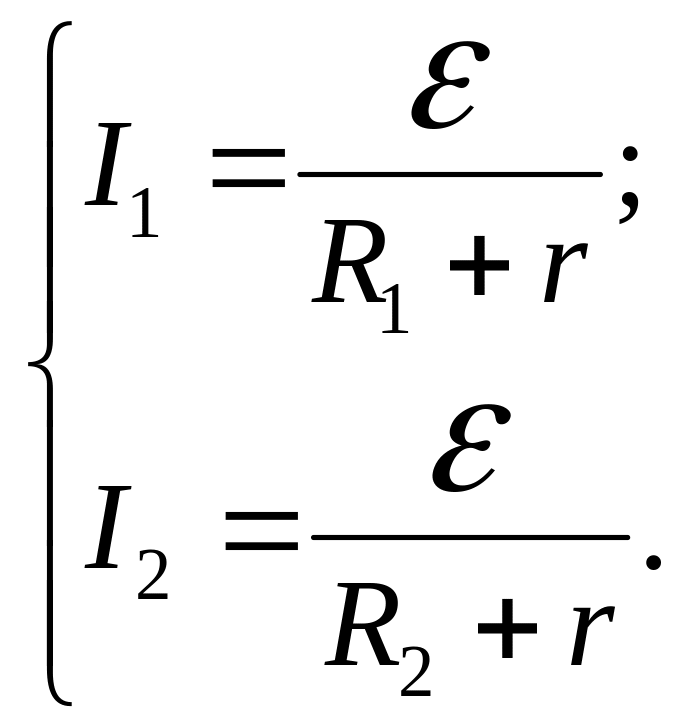 , (3)
, (3)
Для визначення внутрішнього опору джерела струму, знайдемо відношення першого рівняння системи (1) до другого:
![]() . (4)
. (4)
Значення опору підставляємо в одне із рівнянь системи (3) і отримаємо е.р.с. джерела струму:
![]() . (5)
. (5)
Підставляємо з рівняння (4) та з рівняння (5) в рівняння (2) і отримаємо вираз для розрахунку :
= (6)
Зробимо підстановку заданих в умові величин у вираз (6) та отримаємо відповідь:
=
3.125. До джерела струму з е.р.с. = 12 В приєднали зовнішнє навантаження. Напруга на клемах джерела стала при цьому рівною U = 8 В. Визначити у відсотках к.к.д. джерела струму.
3.125.
Дано
= 12 В
U
= 8 В
![]() = ?
= ?
Відношення корисної потужності до загальної потужності визначає ККД джерела струму
![]() . (1)
. (1)
Помножимо чисельник і знаменник рівняння (1) на струм і, користуючісь формулою закону Ома отримаємо вираз для розрахунку к.к.д.:
![]() . (2)
. (2)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.126. Зовнішня ділянка електричного кола споживає потужність Р = 0,75 Вт. Визначити силу струму в мережі, якщо е.р.с. джерела струму становить = 2 В, а його внутрішній опір r = 1 Ом.
3.126.
Дано
= 2 В
r
= 1 Ом Р
= 0,75 Вт
![]() = ?
= ?
З закону Ома для повного кола можна отримати
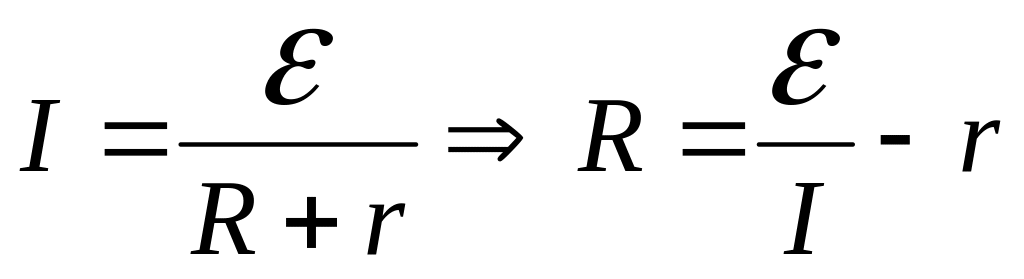 , (1)
, (1)
де — зовнішній опір; — внутрішній опір.
Потужність чисельно дорівнює роботі постійного струму за одиницю часу, тому отримаємо з формули потужності зовнішній опір:
![]() .
(2)
.
(2)
З рівнянь (1) та (2) отримаємо квадратне рівняння
 , (3)
, (3)
Розв’язок якого і є виразом для розрахунку струму:
![]() = (4)
= (4)
Зробимо підстановку заданих в умові величин у вираз (4) та отримаємо відповідь:
=
3.127. Сила струму в провіднику змінюється з часом за законом І = 4 + 2t2. Який заряд проходить через поперечний перетин провідника за проміжок часу від t1 = 2 с до t2 = 6 с?
3.127.
Дано
І
= 4 + 2t2 t1
= 2 с
t2
= 6 с
= ?
Сила електричного струму чисельно дорівнює зміні заряду, перенесеного через поперечний переріз провідника, залежно від часу
. (1)
Звідки можна отримати вираз для визначення електричного заряду, що проходить через перетин провідника за заданий час:
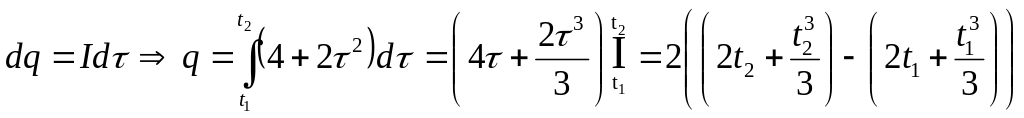 .
(2)
.
(2)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.128. Сила струму в провіднику з опором R = 10 Ом за час t = 50 с рівномірно наростає від I1 = 5 А до І2 = 10 А. Визначити кількість теплоти Q, що виділилося за цей час у провіднику.
3.128.
Дано
R
= 10 Ом
t
= 50 с I1
= 5 А
І2
= 10 А
= ?
Рис. 3.128
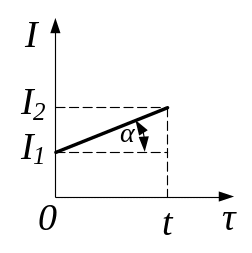
Кількість теплоти
![]() ,
що виділяється в провіднику при
проходженні в ньому постійного струму
(закон Джоуля — Ленца),
,
що виділяється в провіднику при
проходженні в ньому постійного струму
(закон Джоуля — Ленца),
![]() . (1)
. (1)
З рис. 3.128 видно, що рівняння цього графіку буде пряма
![]() . (2)
. (2)
З виразу (1) інтегруванням можна отримати вираз для визначення кількості теплоти, що виділиться в провіднику за заданий час:
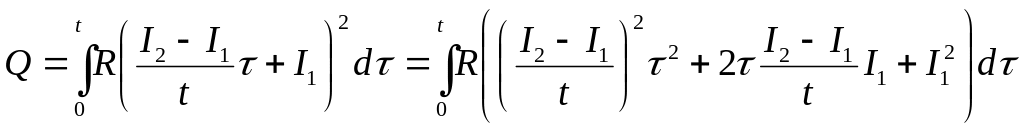 .
.
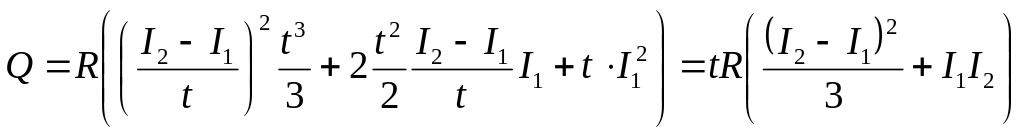 . (3)
. (3)
Зробимо підстановку заданих в умові величин у вираз (3) та отримаємо відповідь:
=
3.129. При рівномірному зростанні сили струму у провіднику від I1 = 1 А до І2 = 2 А за t = 10 секунд виділилася кількість теплоти Q = 5 кДж. Знайти опір R провідника.
3.129.
Дано
I1
= 1 А І2
= 2 А t
= 10 с Q
= 5 кДж
= ?
Рис. 3.129
Кількість теплоти , що виділяється в провіднику при проходженні в ньому постійного струму (закон Джоуля — Ленца),
. (1)
З рис. 3.129 видно, що рівняння цього графіку буде пряма
. (2)
З виразу (1) інтегруванням можна отримати вираз для визначення кількості теплоти, що виділиться в провіднику за заданий час:
.
. (3)
Звідки отримаємо вираз для розрахунку опору
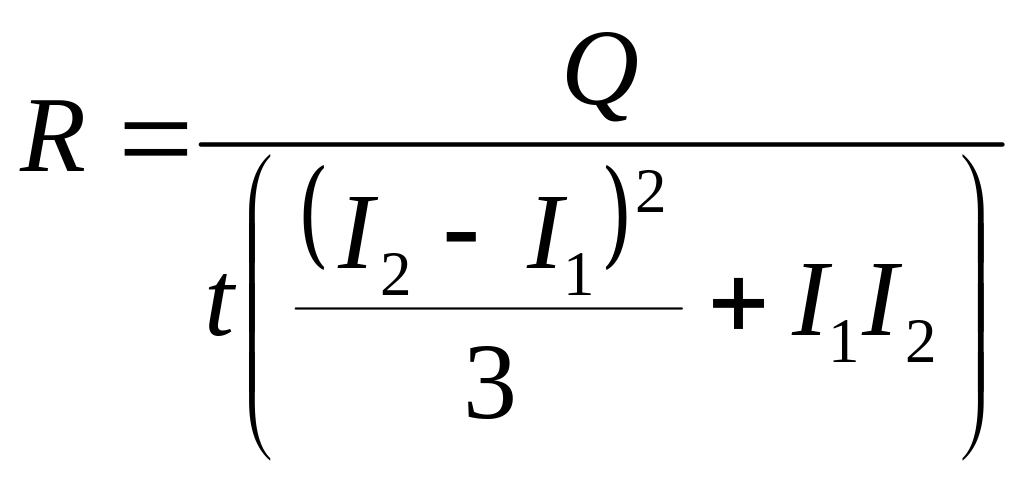 . (4)
. (4)
Зробимо підстановку заданих в умові величин у вираз (4) та отримаємо відповідь:
=
3.130. Який об'єм води
можна закип'ятити, затративши електричну
енергію Q
= 3 ГВт-г? Початкова температура води
![]() = 10°С.
= 10°С.
3.130.
Дано
Q
= 3∙3600∙109
Дж
= 10°С
![]() = 1000 кг/м3
= 1000 кг/м3
![]() = 4190 Дж/(кг∙К)
= 4190 Дж/(кг∙К)
![]() = ?
= ?
Енергія, яка необхідна для нагрівання води визначається за формулою
![]() ,
(1)
,
(1)
де - питома теплоємність.
З формули (1) знаходимо який об'єм води можна закип'ятити
![]() .
(2)
.
(2)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.131. На плитці
потужністю
![]() = 0,5 кВт стоїть чайник, в який налитий
= 1 літр води при температурі
= 16°С. Вода в чайнику закипіла через
=20 хвилин після вмикання плитки. Яка
кількість теплоти Q
при цьому втрачена на нагрівання повітря.
= 0,5 кВт стоїть чайник, в який налитий
= 1 літр води при температурі
= 16°С. Вода в чайнику закипіла через
=20 хвилин після вмикання плитки. Яка
кількість теплоти Q
при цьому втрачена на нагрівання повітря.
3.131.
Дано
= 0,5 кВт
= 1 л
= 16°С
=20 хв
= 1000 кг/м3
= 4190 Дж/(кг∙К)
![]() = ?
= ?
Енергія, яка необхідна для нагрівання води визначається за формулою
![]() ,
(1)
,
(1)
де - питома теплоємність.
Витрачена електрична енергія дорівнює
![]() .
(2)
.
(2)
Кількість теплоти, яка при цьому втрачена на нагрівання повітря
![]() .
(3)
.
(3)
Зробимо підстановку заданих в умові величин у системі одиниць СІ у вираз (3) та отримаємо відповідь:
=
3.132. = 4,5 літра води можна закип'ятити, затративши електричну енергію Q = 0,5 кВт-г. Початкова температура води = 23°С. Знайти к.к.д. нагрівника.
3.132.
Дано
Q
= 0,5 кВт-г
= 4,5 л
= 23°С
= 1000 кг/м3
= 4190 Дж/(кг∙К)
= ?
Енергія, яка необхідна для нагрівання води визначається за формулою
![]() ,
(1)
,
(1)
де - питома теплоємність.
Тоді к.к.д. дорівнює
![]() .
(2)
.
(2)
Зробимо підстановку заданих в умові величин у системі одиниць СІ у вираз (2) та отримаємо відповідь:
=
3.133. Температура водяного термостата об'ємом = 1 літр підтримується постійною за допомогою нагрівника потужністю = 26 Вт. На нагрівання води витрачається = 80% цієї потужності. На скільки знизиться температура води в термостаті за = 10 хвилин, якщо нагрівник вимкнути?
3.133.
Дано
= 1 л
= 26 Вт
= 80%
= 10 хв
= 1000 кг/м3
= 4190 Дж/(кг∙К)
![]() = ?
= ?
Енергія, яка необхідна для нагрівання води визначається за формулою
![]() ,
(1)
,
(1)
де - питома теплоємність.
Тоді к.к.д. дорівнює
![]() .
(2)
.
(2)
З формули (2) отримуємо
![]() .
(2)
.
(2)
Зробимо підстановку заданих в умові величин у системі одиниць СІ у вираз (2) та отримаємо відповідь:
=
3.134. Вольфрамова
нитка електричної лампочки при температурі
![]() = 20°С має опір R1
= 35,8 Ом. Яка буде температура нитки, якщо
при вмиканні лампочки в мережу напругою
= 120 В по ній йде струм
= 0,33 А? Температурний коефіцієнт опору
вольфраму α
=4,6 10-3
К-1.
= 20°С має опір R1
= 35,8 Ом. Яка буде температура нитки, якщо
при вмиканні лампочки в мережу напругою
= 120 В по ній йде струм
= 0,33 А? Температурний коефіцієнт опору
вольфраму α
=4,6 10-3
К-1.
3.134.
Дано
= 20°С
R1
= 35,8 Ом
= 120 В
= 0,33 А α
=4,6 10-3
К-1
![]() = ?
= ?
Питомий опір провідника залежить від його температури
![]() , (1)
, (1)
де
![]() — питомий опір при 0°С;
— питомий опір при 0°С;
![]() — температурний коефіцієнт опору.
— температурний коефіцієнт опору.
Якщо знехтувати зміною розмірів провідника при зміні його температури, то можна записати, для двох температур провідника, значення їхніх опорів:
![]() , (2)
, (2)
де
![]() - опір провідника при 0°С.
- опір провідника при 0°С.
Опір провідника в другому випадку знайдемо за законом Ома, тобто за формулою:
![]() . (3)
. (3)
Підставляємо опір з виразу (3) у систему рівнянь (2) і знайдемо з відношення цих рівнянь шукану температуру
![]() , (4)
, (4)
Зробимо підстановку заданих в умові величин у вираз (4) та отримаємо відповідь:
=
3.135. Обмотка котушки
з мідного дроту при температурі
= 14°С має опір
= 10 Ом. Після проходження струму, опір
обмотки став рівним
= 12,2 Ом. До якої температури
![]() нагрілася обмотка? Температурний
коефіцієнт опору міді α = 4,15 10-3
К-1.
нагрілася обмотка? Температурний
коефіцієнт опору міді α = 4,15 10-3
К-1.
3.135.
Дано
= 14°С
= 10 Ом
= 12,2 Ом α
= 4,15 10-3
К-1
= ?
Питомий опір провідника залежить від його температури
, (1)
де — питомий опір при 0°С; — температурний коефіцієнт опору.
Якщо знехтувати зміною розмірів провідника при зміні його температури, то можна записати, для двох температур провідника, значення їхніх опорів:
, (2)
де - опір провідника при 0°С.
З відношення рівнянь системи (2) знайдемо шукану температуру
![]() , (3)
, (3)
Зробимо підстановку заданих в умові величин у вираз (3) та отримаємо відповідь:
=
3.136. Яку частку е.р.с. елемента живлення складає різниця потенціалів U на його клемах, якщо внутрішній опір елемента r в 10 разів менший зовнішнього опору R.
3.136.
Дано
![]()
![]() = ?
= ?
Відношення корисної потужності до загальної потужності визначає ККД джерела струму
. (1)
Помножимо чисельник і знаменник рівняння (1) на струм і, користуючись формулою закону Ома отримаємо вираз для розрахунку к.к.д.:
. (2)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.137. Від батареї, е.р.с. якої = 600 В, потрібно передати енергію на відстань = 1 км. Потужність, що споживається = 5 кВт. Знайти мінімальні втрати потужності в мережі, якщо діаметр мідних проводів, що використовуються = 0,5 см.
3.137.
Дано
= 600 В
= 1 км
= 5 кВт
= 0,5 см
![]() = ?
= ?
Втрати потужності в мережі визначаємо за формулою
![]() , (1)
, (1)
де
![]() - повна потужність всієї мережі;
- струм у мережі;
- повна потужність всієї мережі;
- струм у мережі;
![]() опір двох провідної мережі;
= 1,7∙10-8
Ом∙м – питомий опір.
опір двох провідної мережі;
= 1,7∙10-8
Ом∙м – питомий опір.
З рівняння (1) складемо квадратне рівняння
![]() , (2)
, (2)
Рішення якого матиме вигляд
![]() , (3)
, (3)
мінімальний струм знаходимо за формулою:
![]() , (4)
, (4)
У формулу втрати потужності в мережі підставляємо значення струму з формули (4):
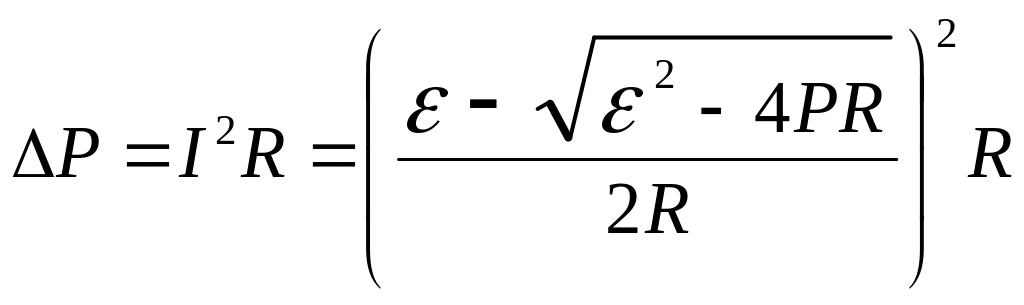 , (5)
, (5)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.138. При зовнішньому опорі R1 = 8 Ом сила струму в електричному колі I1 = 0,8 А, при опорі R2 = 15 Ом сила струму І2 = 0,5 А. Визначити силу струму короткого замикання.
3.138.
Рис. 3.138
Дано
= 8 Ом
= 0,8 А R2
= 15 Ом І2
= 0,5 А
= ?
Зробимо малюнок.
Закон Ома для повного кола має вигляд:
, (1)
де — зовнішній опір; — внутрішній опір.
З рівняння (1) можна зробити висновок, що струм короткого замикання отримаємо, якщо зовнішній опір кола дорівнюватиме нулю:
, (2)
Для визначення параметрів джерела струму: електрорушійної сили і внутрішнього опору, складемо систему рівнянь з формули закону Ома для двох випадків підключення зовнішнього опору:
, (3)
Для визначення внутрішнього опору джерела струму, знайдемо відношення першого рівняння системи (1) до другого:
. (4)
Значення опору підставляємо в одне із рівнянь системи (3) і отримаємо е.р.с. джерела струму:
. (5)
Підставляємо з рівняння (4) та з рівняння (5) в рівняння (2) і отримаємо вираз для розрахунку :
= (6)
Зробимо підстановку заданих в умові величин у вираз (6) та отримаємо відповідь:
=
3.139. Два паралельно з'єднаних елемента живлення з однаковими е.р.с. у = 2 В і внутрішніми опорами r1 = 1 Ом та r2 = 1,5 Ом, замкнені на зовнішній опір R = 1,4 Ом. Знайти струм І в кожному з елементів живлення.
Рис. 3.139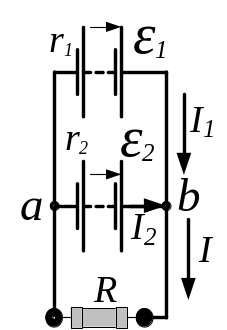
3.139.
Дано
= 2 В r1
= 1 Ом
r2
= 1,5 Ом R
= 1,4 Ом
![]() = ?
= ?
![]() = ?
= ?
Правила Кірхгофа для розгалужених кіл
1. Алгебраїчна сума всіх сил струмів, що сходяться у вузлі розгалуженого кола, дорівнює нулю:
![]() . (1)
. (1)
Струми, що входять у вузол, вважають додатними, які виходять — від'ємними, або навпаки.
2. У будь-якому простому замкненому контурі, довільно обраному у розгалуженому електричному колі, алгебраїчна сума добутків сил струмів на опори відповідних ділянок цього контуру дорівнює алгебраїчній сумі електрорушійних сил, що діють у ньому
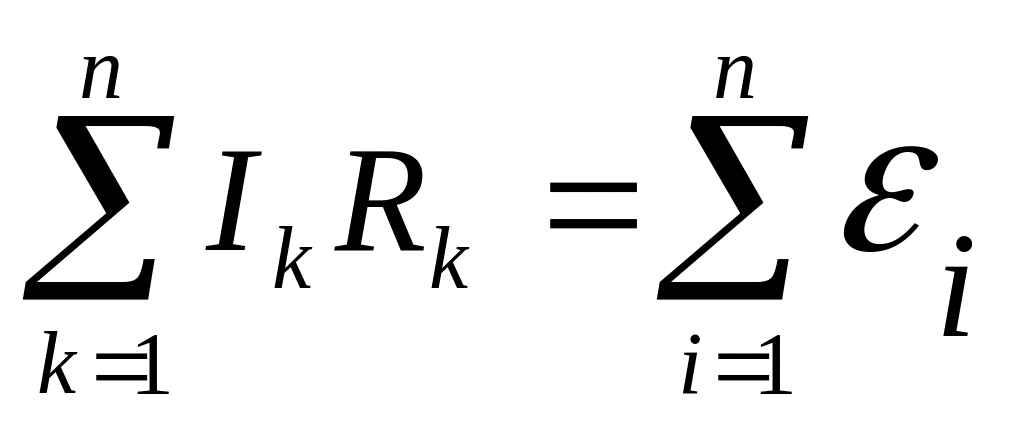 . (2)
. (2)
Для вузла
та для замкнених контурів
![]() і
і
![]() запишемо правила Кірхгофа:
запишемо правила Кірхгофа:
![]() (3)
(3)
Рішення знаходимо за формулами (метод Крамера):
![]() ,
,
![]() ,
,
![]() ,
(4)
,
(4)
де детермінанти дорівнюють:
системи ![]() ; (5)
; (5)
невідомого
![]() ; (6)
; (6)
невідомого
![]() ;
(7)
;
(7)
невідомого
![]() .
(8)
.
(8)
Тоді струми та , знайдемо за формулами (4):
![]() =
=
Напруга на клемах елемента живлення = 2,1 В, опори R1 = 5 Ом, R2 = 6 Ом, R3 = 3 Ом (див. рис, 3.140). Який струм І показує амперметр?
3.140.
Рис. 3.140
Дано
= 2,1 В
= 5 Ом
R2
= 6 Ом R3
= 3 Ом
= ?
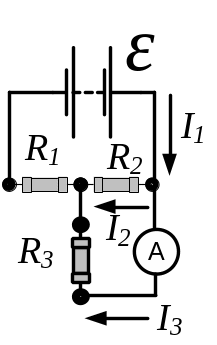
За законом Ома для повного кола, нехтуючи внутрішнім опором джерела струму, можна записати рівняння:
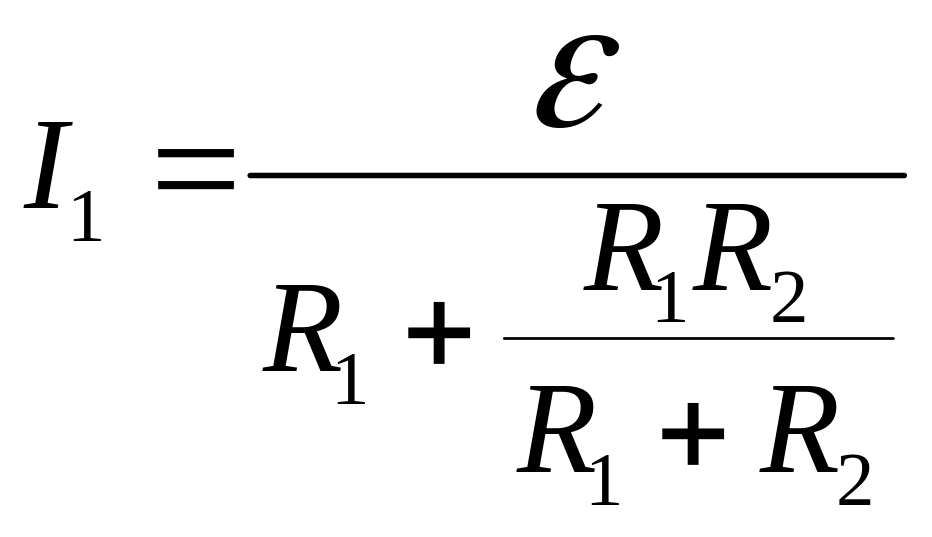 . (1)
. (1)
Тоді напруга на
опорах
![]() та
та
![]() дорівнюватиме
дорівнюватиме
![]() . (2)
. (2)
Визначаємо струм, який показує амперметр
![]() . (3)
. (3)
Зробимо підстановку заданих в умові величин у вираз (3) та отримаємо відповідь:
=
3.141. Елемент живлення, опір і амперметр з'єднані послідовно. Елемент має е.р.с. = 2 В і внутрішній опір = 0,4 Ом. Амперметр показує струм І = 1 А. З яким к.к.д. працює елемент?
3.141.
Дано
= 2 В
= 0,4 Ом І
= 1 А
= ?
Відношення корисної потужності до загальної потужності визначає ККД джерела струму
. (1)
За законом Ома для повного кода можна отримати зовнішній опір:
![]() . (2)
. (2)
Отриманий опір з рівняння (2) підставляємо в формулу (1) і отримаємо вираз для росрахунку к.к.д.:
= (3)
Зробимо підстановку заданих в умові величин у вираз (3) та отримаємо відповідь:
=
Е.р.с. батареї живлення = 100 В, опори R1 = R2 = 40 Ом, R3 = 80 Ом і R4 = 34 Ом. (див. рис. 3.142). Знайти струм I2 що йде через опір R2 і падіння потенціалу U2 на ньому.
3.142.
Рис. 3.142
Дано
= 100 В R1
= R2
= 40 Ом R3
= 80 Ом
R4
= 34 Ом
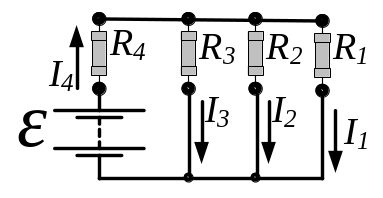
![]() = ? U2
= ?
= ? U2
= ?
За законом Ома для повного кола, нехтуючи внутрішнім опором джерела струму, можна записати рівняння:
 .
(1)
.
(1)
Тоді напруга на опорах , та дорівнюватиме
![]() . (2)
. (2)
Визначаємо струм, який йде через другий опір
![]() . (3)
. (3)
Зробимо підстановку заданих в умові величин у вирази (3) та (2) і отримаємо відповіді:
= U2 =
Е.р.с. батареї живлення = 120 В, опори R3 = 20 Ом, R4 = 25 Ом (див. рис.3.143). Падіння потенціалу на опорі R1 дорівнює = 40 В. Амперметр показує струм
 = 2 А. Знайти
опір R2.
= 2 А. Знайти
опір R2.
3.143.
Рис. 3.143
Дано
= 100 В R3
= 20 Ом,
R4
= 25 Ом
= 40 В
= 2 А
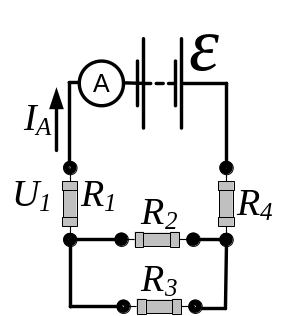
![]() = ?
= ?
За законом Ома для повного кола, нехтуючи внутрішнім опором джерела струму, можна записати рівняння:
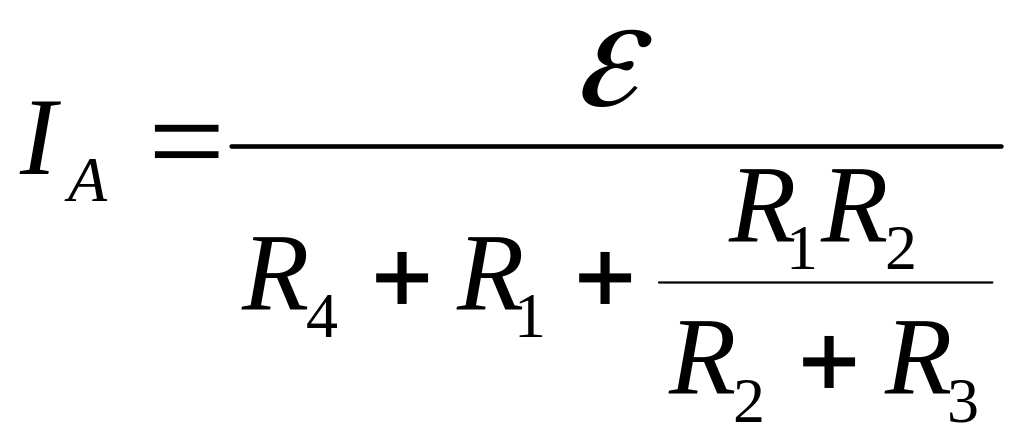 .
(1)
.
(1)
З рівняння (1) визначаємо невідомий опір
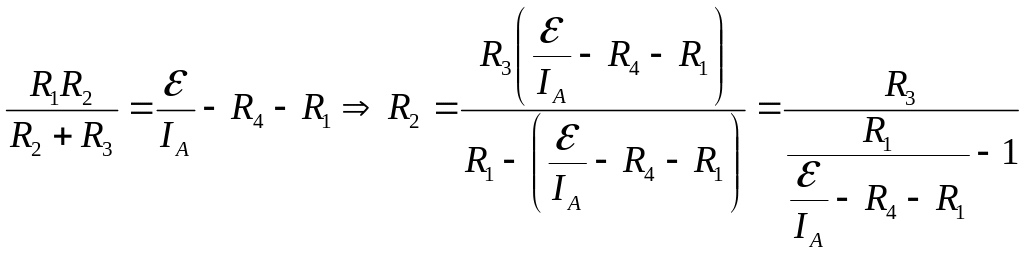 .
(2)
.
(2)
де опір знаходимо за формулою:
![]() . (3)
. (3)
Тоді опор з виразу (3) підставляємо в формулу (2) і отримаємо розрахунковий вираз:
=. (4)
Зробимо підстановку заданих в умові величин у вираз (4) і отримаємо відповіді:
=
Б
Рис. 3.144
атарея з е.р.с. = 10 В і внутрішнім опором = 1 Ом має к.к.д. η = 0,8 (див. рис. 3.144). Падіння потенціалу на опорах R1 і R4 рівні U1 = 4 В і U4 = 2 В. Яку силу струму показує амперметр? Знайти падіння потенціалу на опорі R2.
3.144.
Дано
= 10 В
= 1 Ом η
= 0,8 U1
= 4 В
U4
= 2 В
= ?
= ?
Відношення корисної потужності до загальної потужності визначає ККД джерела струму
![]() , (1)
, (1)
де
- загальний опір зовнішнього кола;
![]() - падіння напруги на зовнішньому опорі.
- падіння напруги на зовнішньому опорі.
З формули (1) отримуємо
![]() , (2)
, (2)
де
![]() - напруга на другому та третьому опорах.
- напруга на другому та третьому опорах.
За законом Ома для повного кола та за формулою к.к.д. можна записати систему рівнянь:
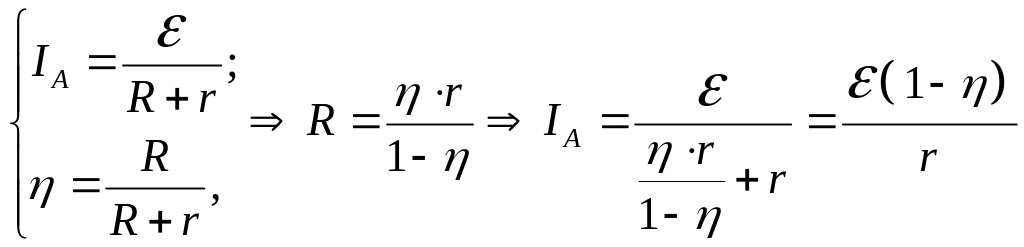 .
(3)
.
(3)
Зробимо підстановку заданих в умові величин у вирази (3) та (2) і отримаємо відповіді:
= =
`
Рис. 3.145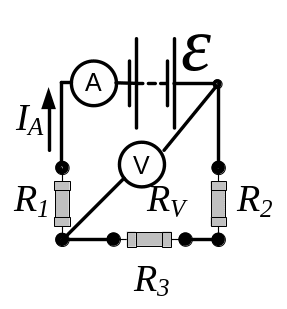
3.145.
Дано
= 100 В R1
= 100 Ом,
R2
= 200 Ом
R3
= 300 Ом,
RV
= 2 кОм
= ?
За законом Ома для повного кола, нехтуючи внутрішнім опором джерела струму, можна записати рівняння:
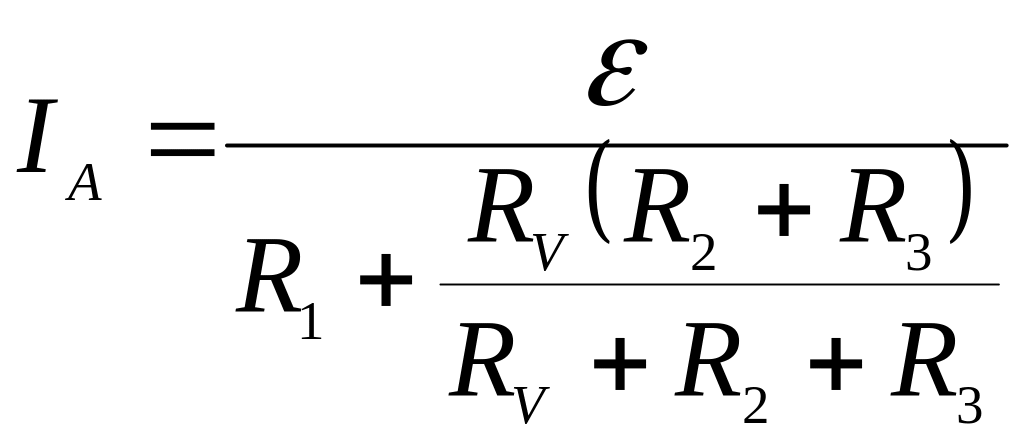 .
(1)
.
(1)
Тоді вольтметр показує напругу
![]() .
(2)
.
(2)
Струм з формули (1) підставляємо у формулу (2) і отримаємо вираз для розрахунку різниці потенціалів U, яку показує вольтметр:
= (3)
Зробимо підстановку заданих в умові величин у вираз (3) і отримаємо відповіді:
=
Опори R1 = R2 = R3 = 200 Ом, опір вольтметра RV = 2 кОм (див рис. 3.146). Вольтметр показує різницю потенціалів U = 100 В. Знайти е.р.с. батареї живлення.
3
Рис. 3.146
Дано
R1
= 200 Ом,
R2
= 200 Ом
R3
= 200 Ом,
RV
= 2 кОм U
= 100 В
= ?
За законом Ома для повного кола, нехтуючи внутрішнім опором джерела струму, можна записати рівняння:
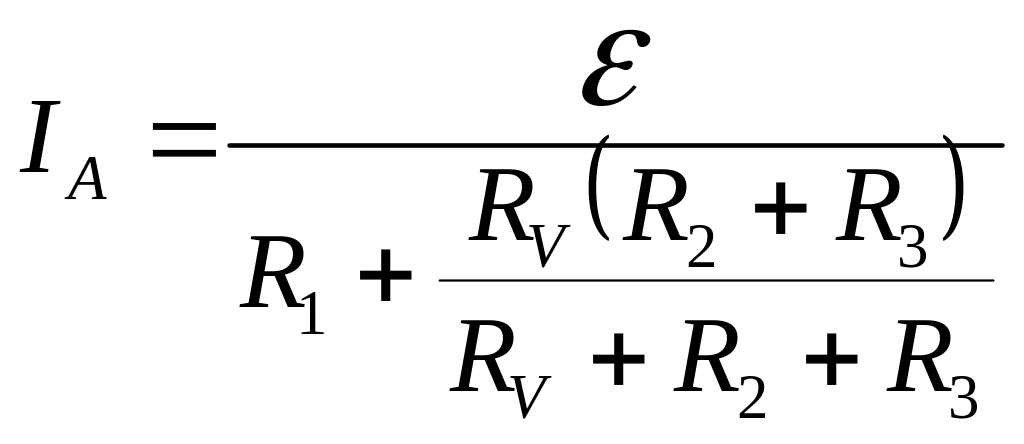 .
(1)
.
(1)
З другого боку загальний струм дорівнює
![]() .
(2)
.
(2)
3 рівнянь (1) і (2) отримаємо вираз для розрахунку відповіді:
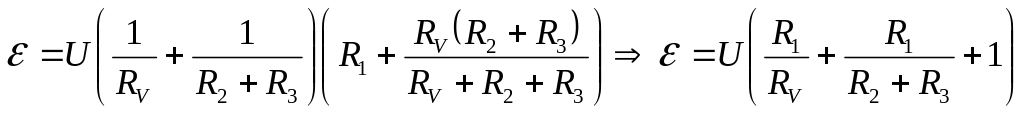 .
(3)
.
(3)
Зробимо підстановку заданих в умові величин у вираз (3) і отримаємо відповіді:
=
3.147. Є = 120-вольтова електрична лампочка потужністю = 40 Вт. Який додатковий опір R треба включити послідовно з лампочкою, щоб вона давала нормальне розжарення при напрузі в мережі U0 = 220 В? Яку довжину ніхромового дроту діаметром = 0,3 мм треба взяти, щоб отримати такий опір?
3.147.
Дано
U
= 120 В
= 40 Вт U0
= 220 В
= 0,3 мм
= ?
=?
Рис. 3.147
Струм в мережі визначимо з потужності лампи:
![]() .
(1)
.
(1)
За законом Ома можна визначити додатковий опір:
![]() .
(2)
.
(2)
Опір циліндричного провідника довжиною та площею поперечного перерізу
![]() , (3)
, (3)
де = 1∙10-6 Ом∙м — питомий опір ніхрому.
Зробимо підстановку заданих в умові величин у вирази (2) та (3) і отримаємо відповіді:
= =
3.148. Від генератора з е.р.с. у = 110 В, потрібно передати енергію на відстань L = 250 м. Потужність, що споживається = 1 кВт. Знайти мінімальний перетин S мідних ( = 1,7∙10-8 Ом∙м) проводів живлення, якщо втрати потужності в мережі не, повинні перевищувати = 1 %.
3.148.
Дано
= 110 В
= 250 м
= 1 кВт
=
/
= 1 %
= ?
Втрати потужності в мережі можна визначити за формулами:
![]() , (1)
, (1)
де
- повна потужність всієї мережі;
- струм у мережі;
![]() опір двох провідної мережі.
опір двох провідної мережі.
З рівняння (1, б) визначаємо струм і підставляємо його в рівняння (1, а)
![]() , (2)
, (2)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.149.
Елемент живлення замикають спочатку
на зовнішній опір
= 2 Ом, а потім на зовнішній опір
= 0,5 Ом. Знайти е.р.с. елемента живлення
і його внутрішній опір r,
якщо відомо, що в кожному з цих випадків
потужність, яка виділяється у зовнішньому
колі, однакова і дорівнює
![]() = 2,54 Вт.
= 2,54 Вт.
3.138.
Рис. 3.138
Дано
= 2 Ом
= 0,5 Ом
= 2,54 Вт
= ?
= ?
Зробимо малюнок.
Потужність чисельно дорівнює роботі постійного струму за одиницю часу
![]() . (1)
. (1)
Користуючись виразом (1) і умовою задачі, складемо рівняння:
![]() . (2)
. (2)
Закон Ома для повного кола має вигляд:
, (3)
де — зовнішній опір; — внутрішній опір.
Для визначення параметрів джерела струму: електрорушійної сили і внутрішнього опору, складемо систему рівнянь з формули закону Ома для двох випадків підключення зовнішнього опору:
, (4)
Для визначення внутрішнього опору джерела струму, знайдемо відношення першого рівняння системи (4) до другого та використаємо формулу (2):
![]() . (5)
. (5)
Значення опору підставляємо в одне із рівнянь системи (3) і отримаємо е.р.с. джерела струму:
![]() . (6)
. (6)
Зробимо підстановку заданих в умові величин у системі одиниць СІ в вирази (6) та (5) і отримаємо відповіді:
= =
3.150. Батареї живлення мають е.р.с. = 2 В та = 4 В, опір R1 = 0,5 Ом (див. рис. 3.150). Падіння потенціалу на опорі R2 дорівнює = 1 В. Знайти, що показує амперметр.
3
3.150
Дано
= 2 В
= 4 В R1
= 0,5 Ом
= 1 В
= ?
