Подходы к решению задач структурного синтеза

Формализация процедур структурного синтеза на каждом иерархическом уровне проводится одним из подходов: 1) перебор; 2)последовательный синтез; 3) трансформация описаний разных аспектов. Классификация алгоритмов структурного синтеза приведена на рисунке 10.

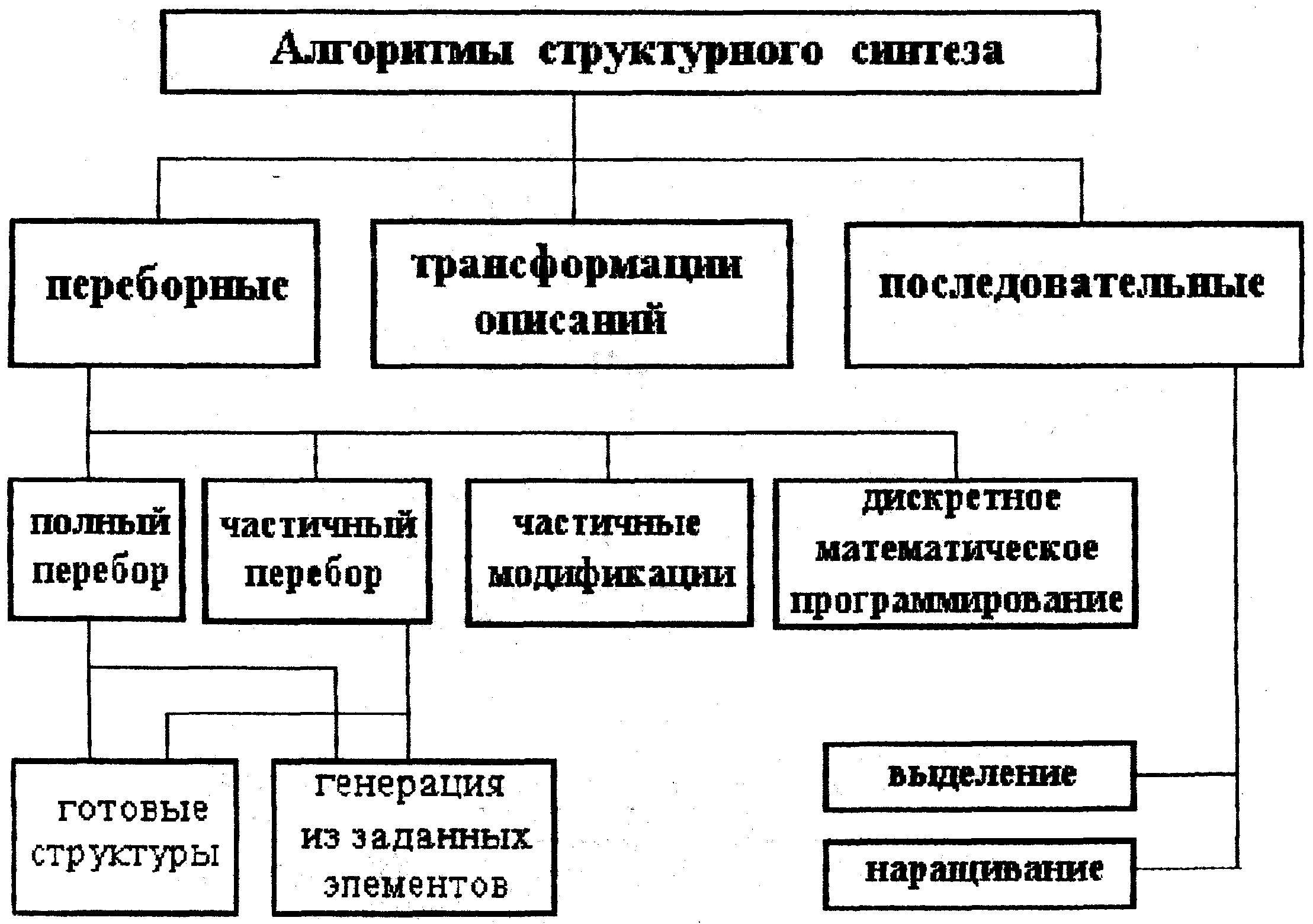
Рисунок 10 - Классификация алгоритмов структурного синтеза

Переборные алгоритмы оценивают только варианты готовых законченных структур. Такие структуры генерируются и хранятся в базах данных. Переборные алгоритмы включают в себя: 1) выбор или генерацию очередного варианта; 2) оценки варианта; 3) принятие решения.

Алгоритмы выбора варианта основываются либо на случайном выборе, либо на эвристических предположениях. Для задач III уровня сложно, а для IV - V невозможно построение множества законченных структур. Автоматизация синтеза сложных структур основана на алгоритмизации процедуры генерации структур из типовых элементов.

Оценка варианта структуры выполняется с помощью параметрического синтеза и анализа. Переборные алгоритмы характеризуются большой трудоемкостью оценок, поэтому они применяются в тех случаях, когда для оценки удается применить упрощенные математические модели.

Принятие решения при переборе основано на сравнении результатов оценки очередного варианта с лучшей из ранее просмотренных структур.

Последовательные алгоритмы характеризуются поэтапным решением задачи синтеза с возможностью оценки промежуточных структур.

При наращивании происходит поочередное добавление элементов к некоторой исходной структуре. За исходную структуру может быть принят какой-либо элемент. Примерами алгоритмов наращивания служат алгоритмы компоновки и размещения.

При выделении из обобщенной избыточной структуры удаляются лишние элементы. Примерами могут служить обобщенные технологические маршруты обработки деталей.

Методы получения математических моделей

Проектирование многих технических объектов связано с необходимостью анализа физических процессов. Примером служит расчет теплообменного оборудования. Основой моделей на микроуровне, применяемых в проектировании теплообменного оборудования, являются дифференциальные уравнения в частных производных.

Напряженное состояние деталей конструкции описывается дифференциальными уравнениями разного вида. Любое из этих уравнений может быть получено из общего квазигармонического уравнения.

(1)

где х, у, z - пространственные координаты,  - искомая функция, Кх, Ку, Кz - коэффициенты, G - внешнее воздействие.

Вторая важная задача проектирования - изучение его гидродинамических свойств. Наиболее общими уравнениями, описывающими этот процесс, являются уравнения Навье-Стокса

(2)

где U - проекции вектора скорости, F - проекции вектора силы, Р - давление,  - плотность,  - вязкость , =/.

Третья задача проектирования - расчет тепловых режимов работы деталей и узлов. Стационарное уравнение теплопроводности имеет вид:

(3)

где Т - температура,  - коэффициенты теплопроводности, Q - источник тепла.

Приведенные выше уравнения имеют множество решений, для получения единственного необходимо задать краевые условия. Сведения об искомых функциях на границах пространственных областей называют граничными условиями, а значения этих же функций в начальный момент времени - начальными условиями. Исходное дифференциальное уравнение с краевыми условиями называется дифференциальной краевой задачей и представляет собой математическую модель исследуемого объекта.

Точное решение можно получить лишь для незначительного числа краевых задач, а общий способ заключается в отыскании приближенного решения. Наиболее широкое распространение получили модели на основе интегральных уравнений и модели на основе метода сеток.

Сущность модели на основе интегральных уравнений заключаются в переходе от уравнений в частных производных к эквивалентному интегральному уравнению и решению его численными методами. Сущность метода сеток состоит в аппроксимации искомой непрерывной функции совокупностью приближенных ее значений, рассчитанных в некоторых точках, узлах. Совокупность узлов и образует сетку. Применение метода сеток позволяет свести дифференциальную краевую задачу к системе нелинейных алгебраических уравнений. В общем случае алгоритм метода сеток состоит из трёх этапов:

1) Построение сетки в заданной области, т.е. дискретизация задачи.

2) Получение системы алгебраических уравнений относительно узловых значений.

3) Решение полученной системы уравнений.

Из сеточных методов наибольшее распространение получили метод конечных элементов и метод конечных разностей. Они отличаются на 1 и 2 этапе, а на третьем полностью одинаковы.