5.2 Таблицы истинности
Все возможные логические значения формулы, в зависимости от значений входящих в нее элементарных высказываний, могут быть описаны полностью с помощью таблицы истинности. Таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы. Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре:
(0, 0), (0, 1), (1, 0), (1, 1).
Таблица 12 – Сводная таблица истинности для двух сложных высказываний
х |
у |
х&у |
х v у |
х→у |
х↔у |
х |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Например, для формулы х v у→х&у таблица истинности имеет вид (таблица 2):
Таблица 13 – Таблица истинности для формулы х v у→х&у
х |
у |
х |
у |
х v у |
х&у |
х v у →х&у |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
Если формула содержит три переменные, то возможных наборов значений переменных восемь:
(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д. Легко видеть, что если формула содержит n элементарных высказываний, то она принимает 2n значений, состоящих из нулей и единиц, т.е. таблица истинности содержит 2n строк.
Например, для формулы a & b v c таблица истинности имеет вид (таблица 3):
Таблица 14 – Таблица истинности для формулы a & b v c
a |
b |
c |
a & b |
a & b v c |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
5.3 Равносильные формулы алгебры логики
Некоторые формулы принимают значение "истина" при любых значениях истинности входящих в них переменных. Таковой будет, например, формула А v Ā, соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
В качестве другого примера рассмотрим формулу А & Ā, которой соответствует, например, высказывание "Катя самая высокая девочка в классе, и в классе есть девочки выше Кати". Очевидно, что эта формула ложна, так как либо А, либо Ā обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными. Равносильность двух формул алгебры логики обозначается символом " ". Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
Важнейшие равносильности алгебры логики можно разбить на три группы.
I. Основные равносильности:
- законы идемпотентности
3. x & 1 x
4. x v 1 1
5. x & 0 0
6. x v 0 x
7. x &
0 – закон противоречия.
8. x v 1 – закон исключенного третьего.
9.
x – закон снятия двойного
отрицания.
- законы поглощения.
II. Равносильности, выражающие одни логические операции через другие:
Замечание. Из равносильностей этой группы следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание.
III. Равносильности, выражающие основные законы алгебры логики:
- коммутативность конъюнкции
- коммутативность дизъюнкции
- дистрибутивность конъюнкции
относительно дизъюнкции.
- дистрибутивность дизъюнкции
относительно конъюнкции.
Используя равносильности I, II, III групп можно часть формулы или формулу заменить равносильной ей формулой. Такие преобразования формул называются равносильными.
Формула А считается проще равносильной В, если она содержит меньше букв, меньше логических операций.
Примеры:
Упростить формулу
.
Запишем цепочку равносильных формул:
Подробнее:
Доказать тождество
Доказать, что формула
тождественно истинная.
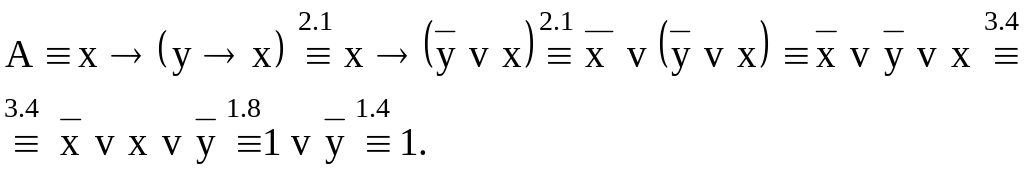
Равносильности III группы говорят о том, что алгебра логики обладает коммутативными и ассоциативными законами относительно операций конъюнкции и дизъюнкции. Эти же законы имеют место и в алгебре чисел. Поэтому над формулами алгебры логики можно производить те же преобразования, которые проводятся в алгебре чисел (раскрытие скобок, заключение в скобки, вынесение за скобки общего множителя).