1.2.4 Логические действия с простыми категорическими суждениями

С суждениями возможны следующие действия: отрицание, превращение, обращение и противопоставление.

Отрицание — это переход к суждению, контрадикторному исходному.

Превращение суждения — логическая операция, в резуль­тате которой одновременно изменяется качество суждения и предикат исходного суждения заменяется на полученный в ре­зультате его отрицания.

Обращение суждения — логическая операция, в результате которой субъект исходного суждения становится предикатом выводного, а предикат исходного — субъектом выводного.

Противопоставление суждения — логическая операция, в результате которой одновременно изменяются качество суж­дения, предикат исходного суждения заменяется на полученный в результате его отрицания и субъект и предикат меняются местами.

Противопоставление суждения, в зависимости от того в каком порядке его осуществлять делится на два вида: противопоставление предикату и противопоставление субъекту.

1.2.5 Отношения между сложными суждениями

Между сложными суждениями существуют отношения – тождества, подчинения, противоположности, подпротивоположности и противоречия. Эти отношения проявляются в соотношении истинностных характеристик сложных суждений.

Тождественными являются суждения, между кото­рыми наблюдаются лишь нелогические различия: лексико-грамматическая или языковая форма выражения.

Подчинение (субординация) — отношение между суждени­ями, истинность одного из которых (подчиняющего) необходимо влечет за собой истинность другого (подчинённого) и наоборот – неистинность подчинённого необходимо влечёт за собой неистинность подчиняющего.

Подпротивоположность (субконтрарность) — отношение между суждениями, которые могут быть одновременно ис­тинными, но не могут быть одновременно неистинными.

Противоположность (контрарность) — отношение между суждениями, которые не могут быть одновременно истинными, но могут быть одновременно неистинными.

Противоречие (контрадикторность) — отношение между суждениями, истинностные характеристики которых не могут совпадать.

1.2.6 Равносильные формулы сложных суждений

Две формулы сложных суждений А и В называются равносильными, если они принимают одинаковые логические значения при любом наборе значений, входящих в формулы элементарных высказываний.

Равносильность формул будем обозначать знаком , а запись А означает, что формулы А и В равносильны.

Например, равносильны формулы:

,

х v х ,

(x^ ) v y .

Формула А называется тождественно истинной (или тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных.

Например, тождественно истинны формулы , .

Формула А называется тождественно ложной, если она принимает значение 0 при всех входящих в нее переменных.

Используя равносильности I, II, III групп можно часть формулы или формулу заменить равносильной ей формулой. Такие преобразования формул называются равносильными.

1.3 Умозаключение

1.3.1 Фигуры, модусы и мнемонические названия модусов

В зависимости от места среднего термина в посылках различают четыре фигуры категорического силлогизма (рисунок 1.2).

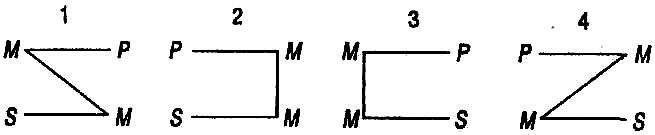
Рисунок 1.2 – Фигуры простого категорического силлогизма

Каждая фигура простого категорического силлогизма в зависимости от качественно-количественной характеристики составляющих его посылок и заключения имеет свои модусы.

Чтобы облегчить логическую процедуру сведения модусов второй, третьей и четвертой фигур к модусам первой, в формальной логике использовали мнемоничес­кий прием, заключавшийся в повторении заглавных и строчных букв латинского алфавита в названиях модусов (таблица 1.2).

Функциональными строчными согласными в названиях моду­сов являются s, p и т.

Если в названии есть согласная s, то для сведения такого модуса необходимо прямое обращение посылки перед этой согласной. Функциональная согласная р обозначает необходимость об­ратить с ограничением или с обобщением находящуюся перед ней посылку, а согласная т — необходимость поменять посылки местами. Наличие в наименовании нескольких функциональных согласных, как в рассмотренном выше модусе Camestres, указы­вает, что требуется выполнить несколько логических действий для сведения к первой фигуре.

Латинские названия правильных модусов простого категоричес­кого силлогизма представлены в сводной таблице (таблице 1.2). В скобках показаны производные от основных модусы, являющиеся правильны­ми только при определенных отношениях терминов в посылках или в заключении.

Таблица 1.2 – Мнемонические названия правильных модусов

I фигура	II фигура	III фигура	IV фигура
Barbara	Baroco	Bocardo	Bramantip
	(Bascara)	(Balasar)	(Barsipan)
	(Birplaza)	(Bariptan)
Celarent	Cesare	(Creiper)	Camenes
	Camestres	(Celaser)	(Cesarsen)
		(Clipermes)	(Cresipen)
Darii	(Dasini)	Datisi	Dimaris
		Darapti	(Dasisin)
		Disamis
Ferio	Festino	Felapton	Fesapo
		Ferison	Fresison
(Gacomo)		(Gradoson)
(Harlee)		(Haversen)
(Kiparis)	(Kisair)
(Locarno)	(Lorsnaco)
(Mizere)