Методические указания к контрольной работе

При решении задач № 1-30 следует познакомиться с методами нахождения пределов функций [1, 5, 6, 8].

Рассмотрим некоторые из них.

Пример. Найти .

Решение. Для нахождения предела отношения двух многочленов относительно при каждый многочлен делят на , где n – наивысшая степень этих многочленов.

,

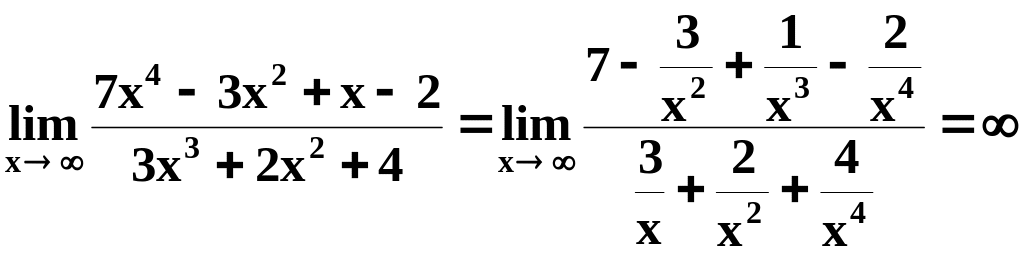так как , где

Пример. Найти .

Решение. Предельный переход даёт нам неопределённость , от которой избавляемся переводом иррациональности из числителя в знаменатель. Используем формулу . Получим

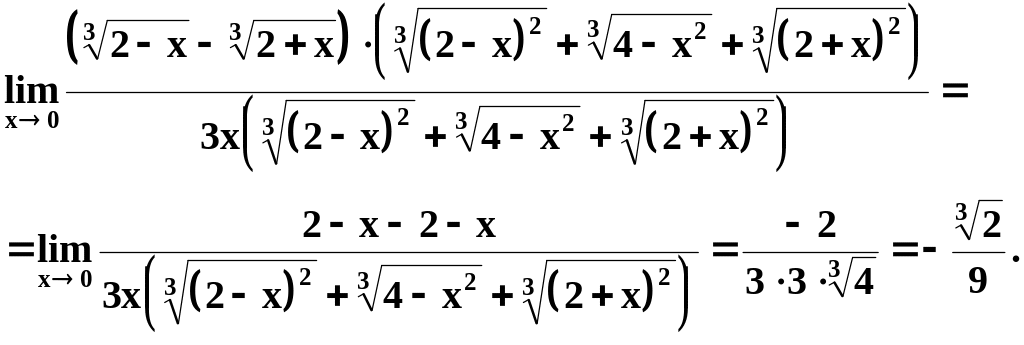
При вычислении пределов, содержащих тригонометрические функции, для раскрытия неопределённости используют первый замечательный предел .

Пример. Найти .

Решение.

.

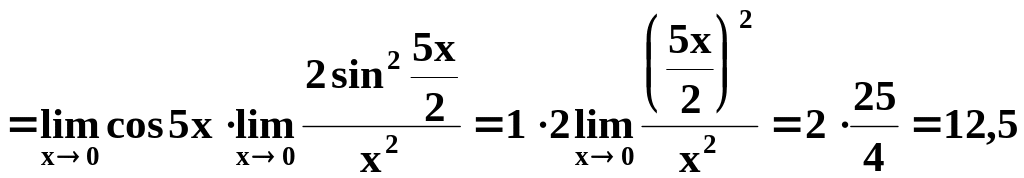Второй замечательный предел вида или используют при раскрытии неопределённости вида .

Пример. Вычислить .

Решение. .

Введём новую переменную , тогда при , получим

.

Для решения задач № 31-60 следует использовать литературу [1, 5, 6, 8].

Пример. Для функции найти значения производных и при .

Решение. .

.

.

.

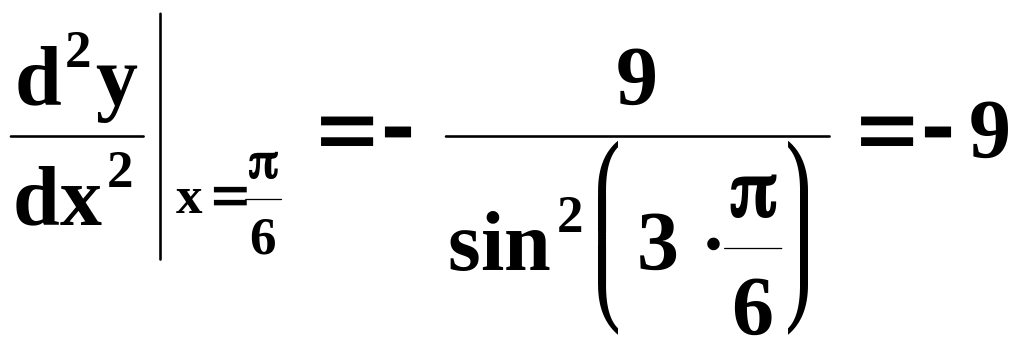В задачах № 61-90 требуется провести полное исследование указанных функций и построить их графики. Эти вопросы освещены в следующей литературе [1, 5, 6, 8].

При исследовании целесообразно придерживаться следующей схемы:

1. найти область определения функции, вычислить предельные значения на её границе, найти уравнения вертикальных и наклонных асимптот, если они существуют. Найти точки пересечения графика с осями координат;

2. с помощью первой производной найти интервалы возрастания и убывания функции, её экстремумы;

3. с помощью второй производной определить интервалы выпуклости и вогнутости графика функции и точки перегиба.

Рекомендуется построение графика функции проводить поэтапно параллельно с исследованием по указанной схеме.

Пример. Построить график функции .

Решение. 1. Функция определена при всех и непрерывна в области определения, следовательно, нет вертикальных асимптот. Найдём уравнение наклонной асимптоты , где

,

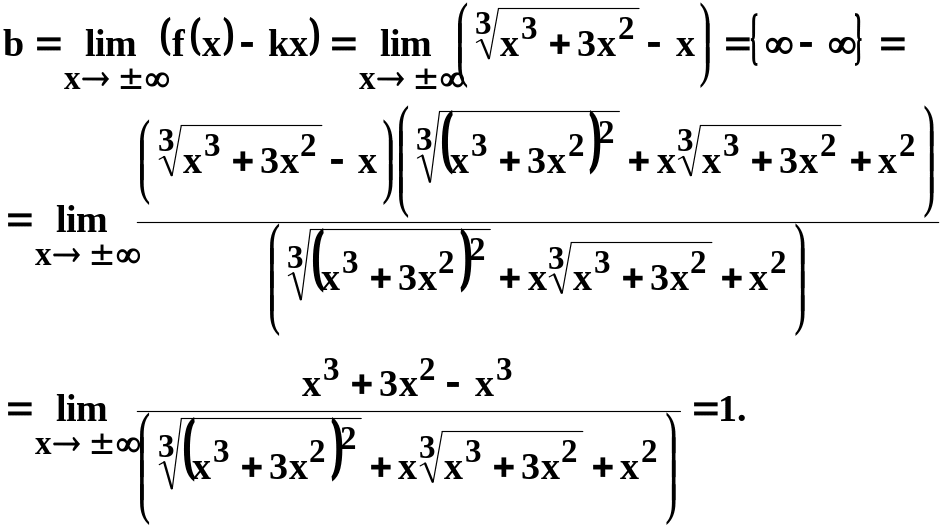
Получили уравнение наклонной асимптоты . Функция пересекает ось ординат при и ось абсцисс при и .

Функция не обладает свойствами чётности, нечётности и периодичности.

2. Определим интервалы возрастания и убывания функции и её

экстремумы, для чего находим первую производную:

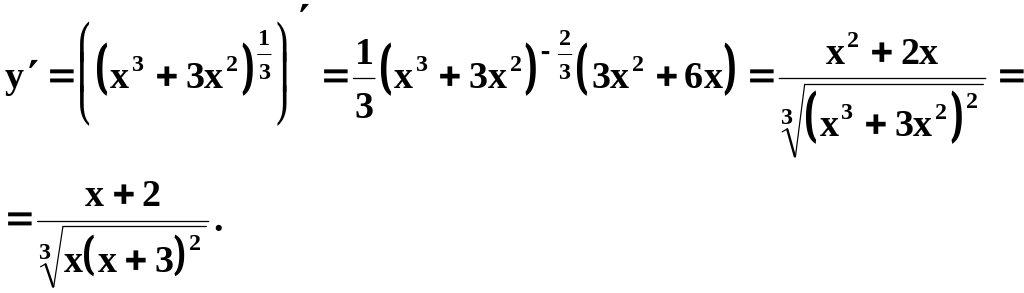
при и производная не существует при . Эти критические точки разбивают область определения на интервалы:

.

Внутри каждого интервала знак производной сохраняется. Чтобы определить знак производной на каждом интервале, выбираем в каждом из них по одной точке и вычисляем значение производной в этих точках. Например, в интервале возьмём точку , тогда , следовательно, функция на интервале возрастает. На интервале функция возрастает, так как . На интервале функция убывает, так как . На интервале функция возрастает, так как .

Составим для наглядности таблицу изменения знаков производной:

		-3		-2		0
	+	не суще- ствует	+	0	-	не суще- ствует	+
	возрас- тает	нет эк-стрему-ма	возрас- тает	макси- мум	убыва- ет	мини-мум	Возра-стает

3. Определим интервалы выпуклости, вогнутости, точки перегиба графика функции, для чего найдём вторую производную:

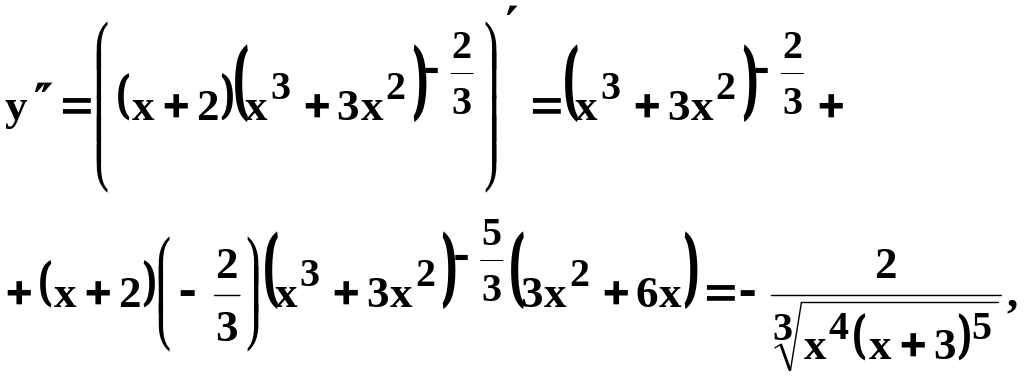
которая не равна нулю для любого конечного . Поэтому точками перегиба могут быть те точки, в которых не существует, то есть . Определим знак второй производной в каждом из интервалов, на которые найденные критические точки разбивают область определения, и составим таблицу изменения знаков второй производной:

		-3		0
	+	не сущест-вует	-	не сущест- вует	-
	кривая вогнута	точка перегиба	кривая выпукла	нет точки перегиба	Кривая выпукла

По результатам исследования строим график функции:

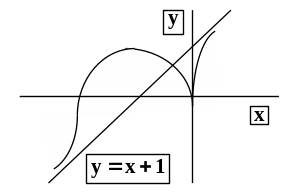
Для вычисления неопределённых интегралов № 91-120 необходимо проработать литературу: [2, 5, 7, 9], где содержатся практические рекомендации по данной теме.

Для выполнения заданий 91-120 (пункт а) нужно из таблицы интегралов выбрать такой, к которому можно свести данный интеграл.

Например, при вычислении

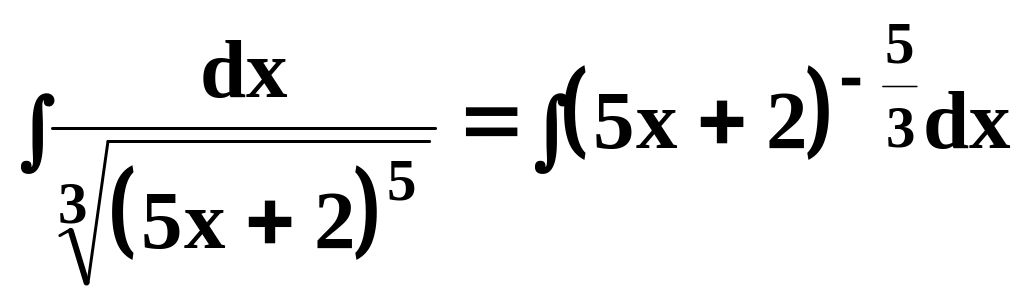
используем табличный интеграл

.

Согласно этой формуле подводим под знак дифференциала основание степени. Так как , то умножим и разделим интеграл на 5, то есть

.

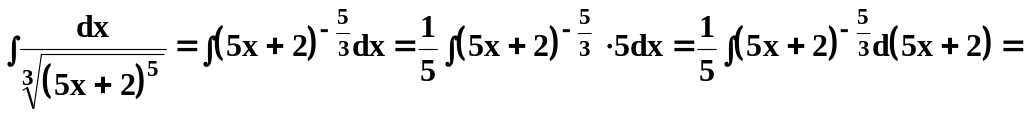
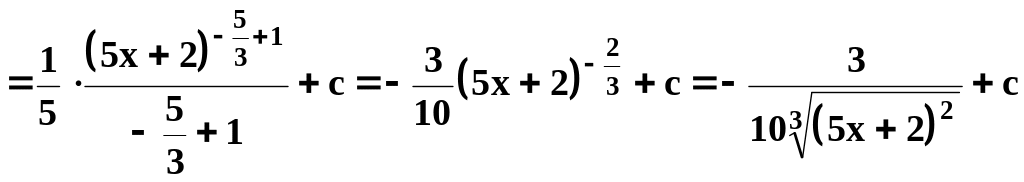Интеграл сводится к табличному путём подведения под знак дифференциала показателя степени . Таким образом:

.

В примере используем формулу , где под знаком дифференциала находится знаменатель дроби. Так как , то

.

При вычислении интегралов в пункте б) применяются методы подстановки и интегрирования по частям, то есть по формуле мы от исходного интеграла переходим к более простому .

Пример. , то есть возьмём

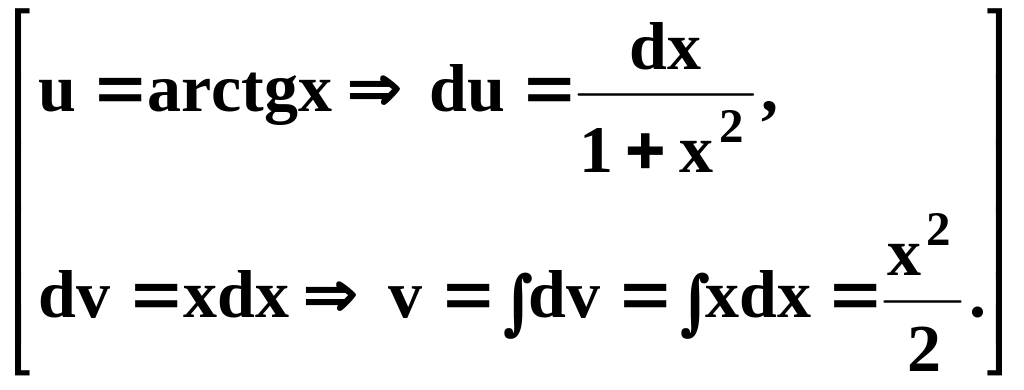
(здесь при нахождении константу полагаем равной 0). Получим

.

Возьмём отдельно:

.

Итак,

.

Пример. Найти . Пусть

.

.

Для нахождения площадей плоских фигур в задачах № 121-150 рекомендуется изучить литературу [2, 5, 7, 9].

При вычислении интегралов в этих задачах и в дальнейшем можно пользоваться таблицей интегралов в справочниках.

Пример. Найти площади частей, на которые круг делится параболой .

Найдём точки пересечения этих линий

В точке пересечения . Площадь меньшей части

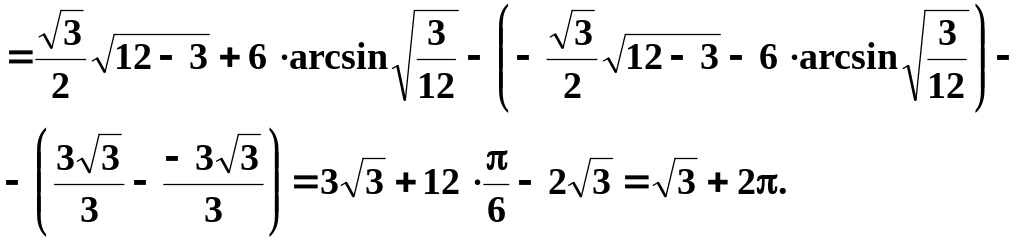
Площадь большей части .