5.5 Сложный теплообмен и теплопередача

5.5.1 Сложный теплообмен

Рассмотренные элементарные виды теплообмена (теплопроводность, конвекция и тепловое излучение) на практике, как правило, протекают одновременно. Конвекция, например, всегда сопровождается теплопроводностью, излучение часто сопровождается конвекцией. Сочетание различных видов теплообмена может быть весьма разнообразным, и роль их в общем процессе неодинакова. Это так называемый сложный теплообмен. Процесс теплообмена между стенкой и омывающим ее газом является типичным примером сложного теплообмена — совместного действия конвекции, теплопроводности и теплового излучения.

В теплотехнических расчетах при сложном теплообмене часто пользуются общим (суммарным) коэффициентом теплоотдачи представляющим собой сумму коэффициентов теплоотдачи соприкосновением, учитывающим действие конвекции, теплопроводности и излучения , т. е.

(31)

В этом случае расчетная формула для определения теплового потока q, Вт/м², имеет вид

. (32)

Если стенка омывается капельной жидкостью, например водой, то

и . (33)

5.5.2 Теплопередача

В теплотехнике часто тепловой поток от одной жидкости (или газа) к другой передается через стенку. Такой суммарный процесс теплообмена, в котором теплоотдача соприкосновением является не­обходимой составной частью, называется теплопередачей. Расчетные уравнения теплопередачи зависят от формы стенки, разделяющей теплоносители.

Р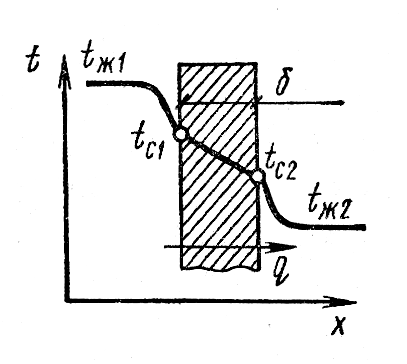 ассмотрим теплопередачу через плоскую однослойную стенку. Примем, что тепловой поток направлен слева направо, температура нагретой среды , температура холодной среды . Температуры поверхностей стенки неизвестны: обозначим их буквами и (рисунок 5).

Рисунок 5 Схема распределения температур при теплопередаче через плоскую стенку

Передача теплоты в рассматриваемом примере представляет собой процесс сложного теплообмена и состоит как бы из трех этапов: теплоотдача от нагретой среди (жидкости или газа) к левой поверхности стенки, теплопроводность через стенку и теплоотдача от правой поверхности стенки к холодной среде (жидкости или газу). При этом, очевидно, поверхностные плотности тепловых потоков в трех указанных этапах одни и те же, если стенка плоская и режим теплообмена стационарный.

Напишем три известных уравнения теплового потока.

1. Уравнение теплоотдачи от нагретой среды (жидкости или газа) к поверхности стенки

. (34)

2. Уравнение теплопроводности через стенку

. (35)

3. Уравнение теплоотдачи от правой поверхности стенки к холодной среде (жидкости или газу)

. (34)

Решив эти уравнения относительно частных температурных напоров, получим:

(35)

Сложив почленно эти уравнения, получим полный температурный напор

(36)

откуда поверхностная плотность теплового потока

(37)

Величина k называется коэффициентом теплопередачи и представляет собой мощность теплового потока, проходящего от более нагретой среды к менее нагретой через 1 м² поверхности стенки за 1 ч при разнице температур между средами 1 °С.

Величина, обратная коэффициенту теплопередачи, называется термическим сопротивлением теплопередаче и обозначается R, м²К/Вт.

Согласно определению k и R, имеем

. (38)

Эта формула показывает, что общее термическое сопротивление равно сумме частных.

Из уравнения (35) можно получить:

(39)

По этим уравнениям можно вычислить температуры по направлению теплового потока при теплопередаче через однослойную стенку.

Если стенка не однослойная, а состоит из нескольких слоев с различной толщиной и коэффициенты теплопроводности , то аналогично формулам (37) и (38) будем иметь:

(40)

(41)

(42)

где — сумма термических сопротивлений слоев плоской стенки.

Количество теплоты Q, Вт, переходящей от одной среды к другой через площадь F любой стенки за 1 ч, будет равно

Для расчета теплового потока при теплопередаче через цилиндрическую стенку незначительной толщины можно, как и при оценке теплопроводности, пользоваться формулами для плоской стенки. Только при большой разности диаметров (например, для труб, покрытых тол­стым слоем изоляции), когда соотношение , эти формулы неприменимы.

23