Критерий Колмогорова

^{Для определения критерия Колмогорова статистическую кривую частот преобразуют в статистическую интегральную функцию и далее критерий Колмогорова вычисляется в следующей последовательности:}

^{1. Определение наибольшей разности частот между экспериментальной статистической интегральной кривой и соответствующей теоретической интегральной кривой:}

^{D0 = max (эί –тί ) (1)}

^{2. Определение коэффициента вероятности λ:}

^{λ = D0 √N (2)}

^{3. Определение величины вероятности Рλ, = 1 – Кλ, по значения λ из табл. 28 источника [1, с. 161].}

^{4. Определяе адекватности. Адекватность удовлетворяется , если Рλ,>0,05, т.е. экспериментальные данные подтверждают теоретическое распределение.}

^{ЗАДАНИЕ}

^{Применить критерий Колмогорова для определения адекватности полученных экспериментальных данных, представленных в табл 1. Условия для выполнения задания представлены в табл.2}

^{Таблица 1.}

^{Результаты экспериментов}

№ опыта (n)	Экспериментальные значения, № серии ( m)						Теорети-ческие значения, (их частота) Уiт
	1	2	3	4	5
1	13,8	17	17,53	15,8	16,1	16 (0,001)_
2	24,6	24,53	24,3	25,1	23,6	24 (0,003)
3	31,9	31,6	31,2	33,45	33,1	32 (0,002)
4	39,3	39,8	40,5	39,7	40,74	40 (0,004)
5	48,6	46,7	48,1	48,2	47,7	48 (0,003)
6	55,3	56,98	55,38	54,3	55,8	56 (0,005)
7	63,8	64,4	63,9	64,12	63,7	64 (0,006)

^{Таблица 2.}

^{Условия для выполнения задания по вариантам}

№ вариан- та	Количество опытов, n (начиная с первого)	Количество серий, m	№ вариан- та	Количество опытов, n (начиная с последнего	)Количество опытов, n (начиная с последнего
1	3	5	11	3	5
2	4	5	12	4	5
3	5	5	13	5	5
4	6	5	14	6	5
5	7	5	15	7	5
6	4	4	16	4	4
7	5	4	17	5	4
8	6	4	18	6	4
9	7	4	19	7	4
10	7	3	20	3	4

^Пример

^{Рассмотрим пример выполнения практической работы в продукте програмного обеспечения Microsoft Excel. Данная работа выполняется в следующей последовательности:}

1. ^{Заносим данные в ячейки (создаем таблицу как в задании)}

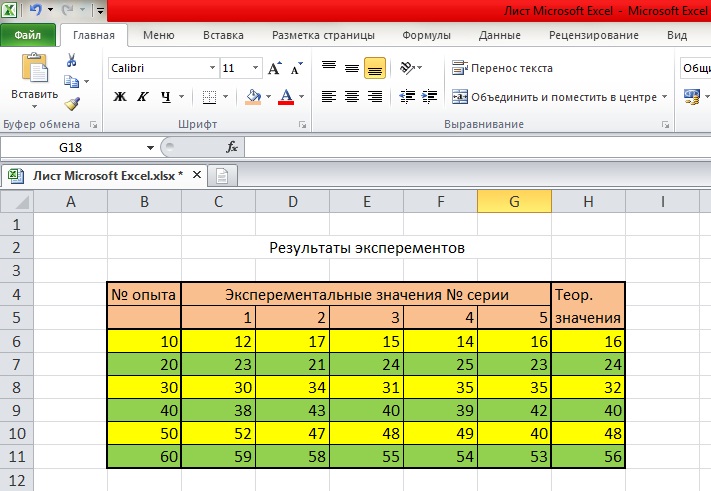
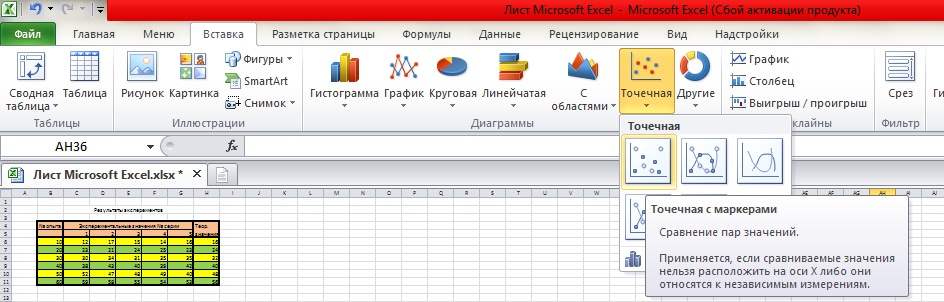
2. ^{Для создания графика переходим в вставка↔точечная диаграмма↔точечная с маркерами. В итоге чего получаем область построения графика.}

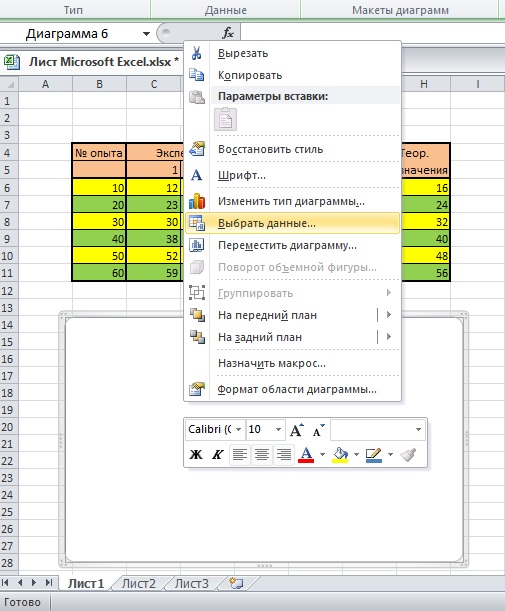
3. ^{На полученную область наводим курсор «мышки» правой клавишей вызываем меню, пункт «выбрать данные»}

4. ^{Далее вносим данные в нужные строки. По оси «у» вносятся номера опытов (для получения компактного графика к номерам опытов добавили цифру «0»), в качестве значений по оси «х» вносим эксперементальные значения одной из серий (в нашем примере использованы значения серии №1 (12-59). Для сравнения эксперементальных значений и теоретических нам необходимо ввести в этом же графике точки теоретических значений. Для оси «у» используем номера опытов, для оси «х» вносим теоретические значения ( в примере значения 16-56). В итоге получим:}

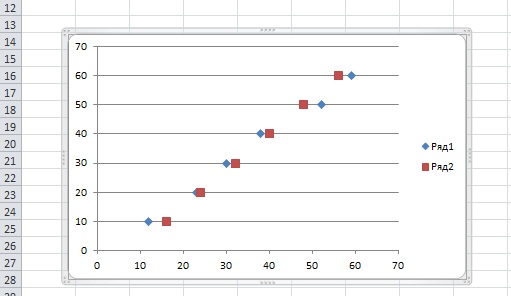
5. ^{Далее необходимо найти зависимость между точками каждого из ряда. Для этого на области графика выбираем любую точку ряда, правой клавишей «мышки» вызываем контекстное меню находим пункт «создать линию тренда»↔ «поместить на диаграмму величину достоверности аппроксимации (R 2)» , выбирая тип диаграммы ориентируемся на то, чтобы значение R2 было наиболее приближено к 1.}

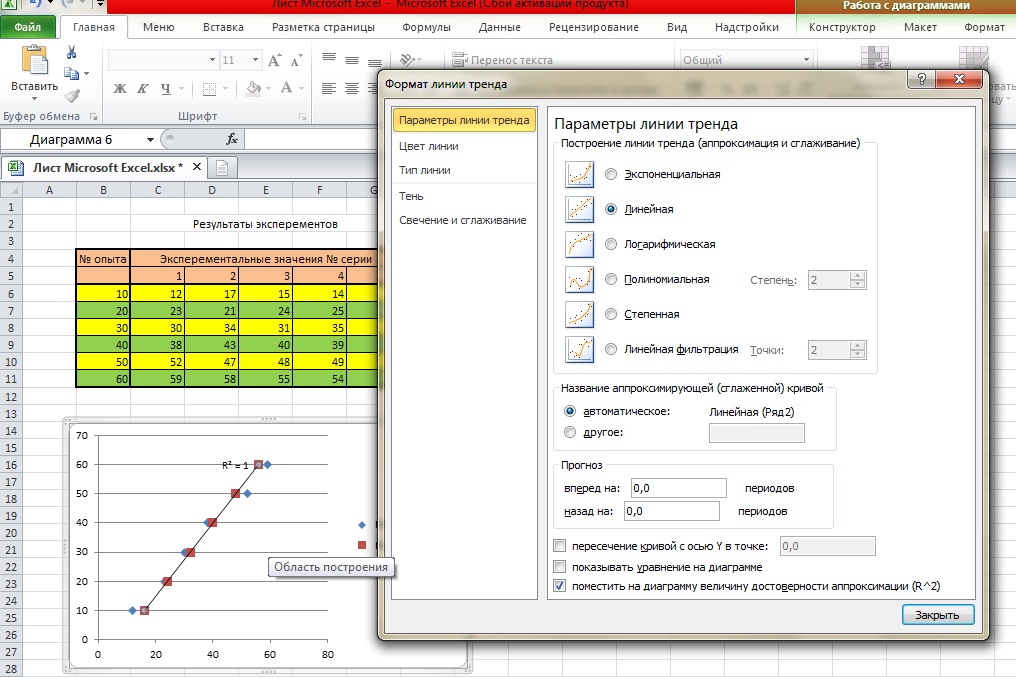
^{Аналогично проводим построение для другого ряда. В итоге получаем:}

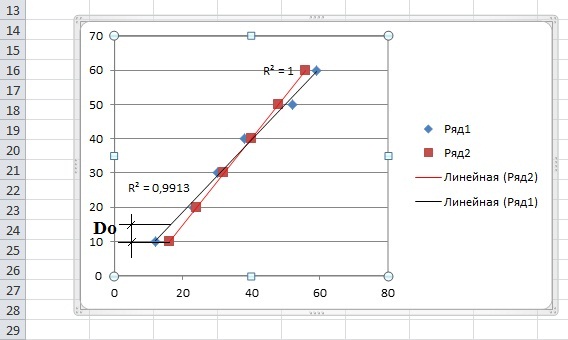
^{6. Определение наибольшей разности частот между экспериментальной статистической интегральной кривой и соответствующей теоретической интегральной кривой производим графически. Эта величина соответствует максимальному расхождению линий по оси «у». Получив значения с 5-ти графиков находим среднее арифмитическое, после чего делим это значение на 10, для того чтобы вернуться к прежнему значению в нашем случае D0 = 0,076}

^{7. Определение коэффициента вероятности λ:}

^{λ = 0,076∙ √30=0,418 (2)}

^{8. Определение величины вероятности Рλ, = 1 – Кλ, по значению λ из табл. 28 источника [1, с. 161]. Рλ = 0,9943}

^{9. Определение адекватности. Адекватность удовлетворяется , если Рλ,>0,05, т.е. экспериментальные данные подтверждают теоретическое распределение.}

^{0,9943>0,05- адекватность удовлетворяется.}

^{Таблица 28. Значение 1 – Кλ}

λ	1	3	5	7	9
0,3	0,9999	0,9999	0,9997	0,9992	0,9981
0,4	0,9960	0,9926	0,9874	0,9800	0,9700
0,5	0,9572	0,9415	0,9228	0,9013	0,8772