13. Энергетический принцип разрушения. Интенсивность выделения энергии

По Гриффитсу -условие роста трещины на (da): система должна выделить (dU/da) дополнительную энергию необходимую для образования трещины размером da: Работа внешних сил F расходуется на упругую энергию пластины U и –энергия для образования трещины. Условия равновесия W d(U–F+W ) /da = 0;

d(F–U)/da = dW /da= G

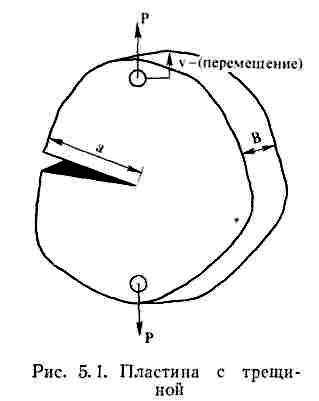
Интенсивность выделения энергии G. Если края трещины свободно перемещаются, то внешние силы совершают работу F= Рdv (нагрузка на перемещение). Для пластины единичной толщины условия роста трещины: G интенсивность выделения энергии (сила распространения трещины) = R сопротивлению росту трещины: G = R, где G = d (F–U)/da; R=dW/da. Полная упругая энергия пластины толщиной В: G = – 1/В(dU/da), (–) условия нагружения. Для пластины без трещины L,W‘, B, E – длина, ширина, толщина образца, модуль Юнга. Из диаграммы Р – v упругая энергия U = Pv /2, где v-перемещение. При наличии трещины определяют податливость С = L/(W‘B E). тогда,

G = 1/В(Рdv/da – dU/da) подставляя перемещение v = CP, а упругая энергия U = PСР/2, получим:

Интенсивность выделения упругой энергии

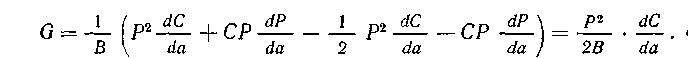
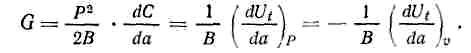
Р =const, то упругая энергия dU увеличивается (края трещины свободно перемещаются).

v = 0, dU уменьшается (нет перемещений), края трещины защемлены. Интенсивность выделения упругой энергии для плоского напряженного состояния:

14. Построение кругов Мора. Влияние толщины образца на процесс разрушения

Круг Мора — это круговая диаграмма, дающая наглядное представление о напряжениях в различных сечениях, проходящих через данную точку. диаграмма Мора характеризует напряженное состояние в точке. Для плоского напряженного состояния (п.н.с.) σ1> σ2 > σ3 = 0 τ max= σ1 / 2

Для плоской деформации (п.д.) σ1> σ2 > σ3 τ max= (σ1 - σ 3) / 2

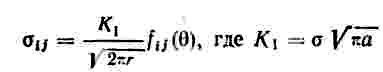
Подставляя значение главных напряжений в формулу и проведя дифференциирование по θ, получим угол θ, при котором касательные напряжения достигают максимального значения. Определив направление главных осей σ1,σ2, находят плоскость в которой действуют τ max.

Влияние толщины на размер зоны пластичности

Толщина пластины играет сущ-ую роль на напряженно-деформируемое состояние при вершине трещины.

r / B«1 - плоская деформация

r / B→1 - плоско – напряженное состояние

при испытаниях:

r / B ≈ 0,025

r ≈ (К1) 2 / σys 2

20. Плосконапряженное состояние, плоская деформация. Влияние толщины образца на к1с

Зона пластичности для ПД < (в 10 раз при θ=0, ν=1/3) чем для ПНС. Методами непосредственного наблюдения процесса разрушения в отраженном свете полированных поверхностей зафиксированы зоны у вершины трещины, величина которых зависит от действующего напряжения, σys материала. Угол наклона зон от 69 до 100 градусов.

Для того, чтобы в материале с низким σys и высокой прочностью (высокая интенсивность напряжений) установилась ПД требуется большая толщина, чем в низкопрочном материале с высоким σys . Разница в зоне пластичности при ПНС и ПД возникает т.к. эффективный σys в 3 раза > σys, полученного при одноосных испытаниях.

Вязкость разрушения определяют при испытании образцов с трещиной (тонким надрезом) на 3х или 4х точечный изгиб. При этом в зоне трещины действуют напряжения на разрыв.

При разрушении сколом (ПД при r / B ≈ 0,025) размер зоны пластичности пропорционален ≈ (К1)\ 2 / σys\ 2

Материал с низким σys и высокой прочностью (высокое К1) требует образцов большей толщины В для создания плоской деформации, чем низкопрочный материал с высоким σys.

Испытание на вязкость разрушения с низким σys и высоким К1с проводят на пластине с соответствующей толщиной.