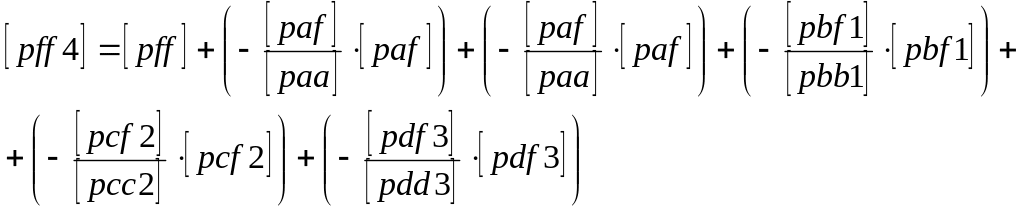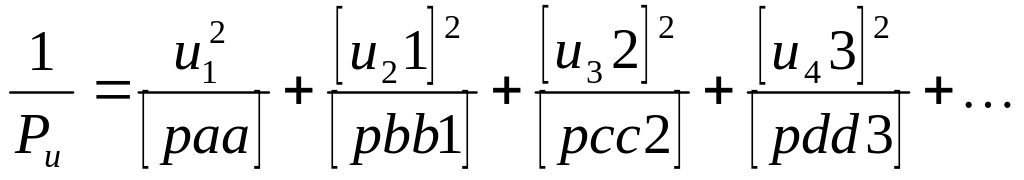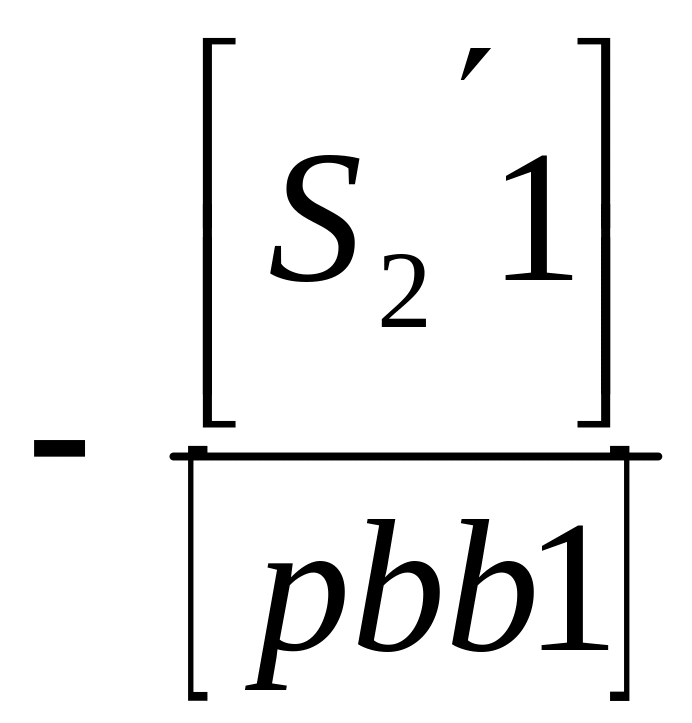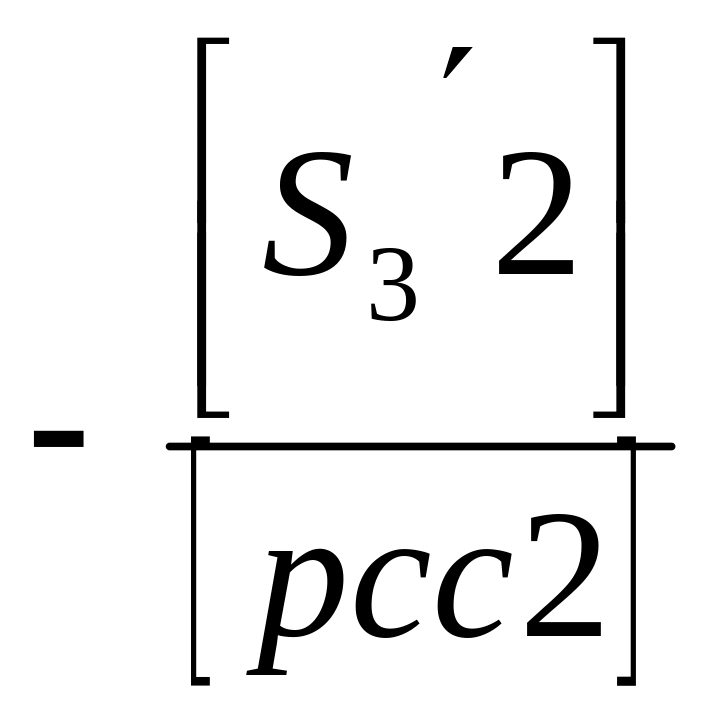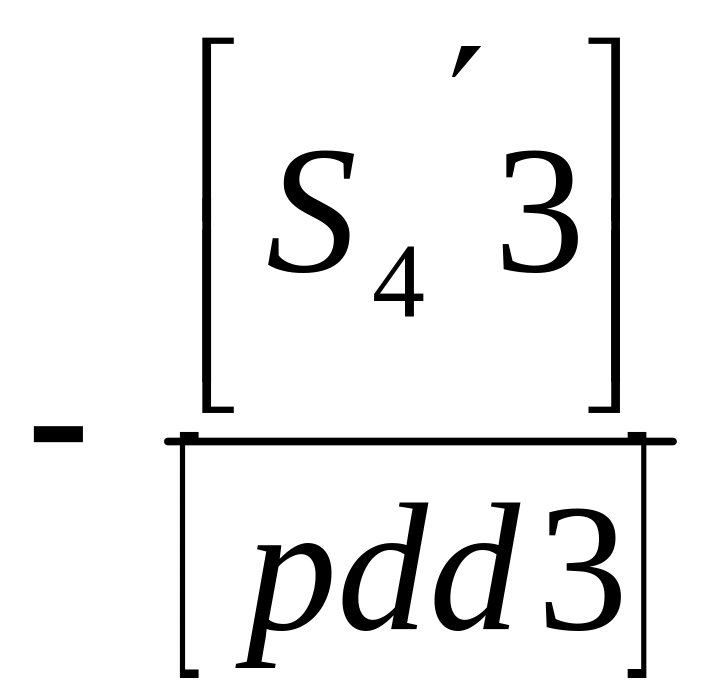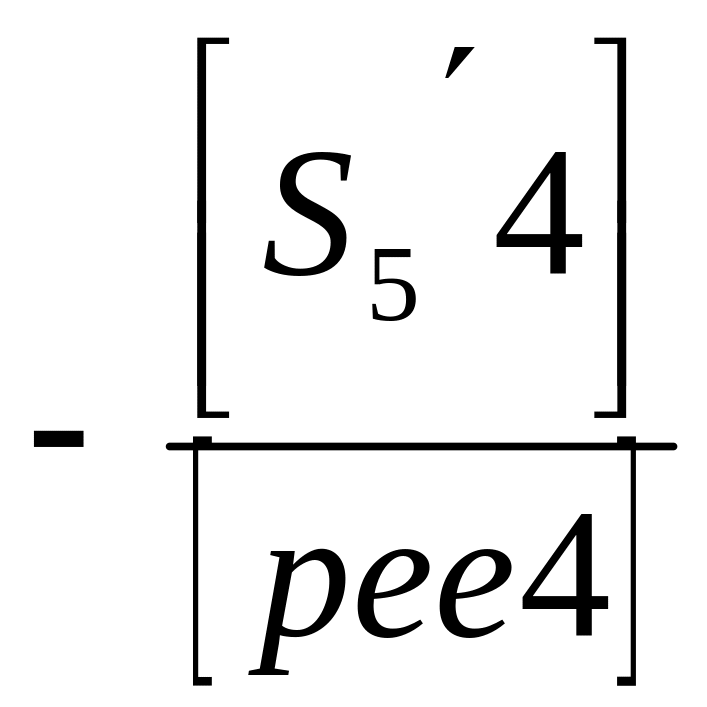Оценка точности

1. Определение ошибки единицы веса. СКО определяется по формуле:

,

где  – поправки в направления;;

n – число всех измеренных направлений;

k – число определяемых пунктов;

q – число исходных пунктов.

Для рассматриваемой сети:

• число всех измеренных направлений ;

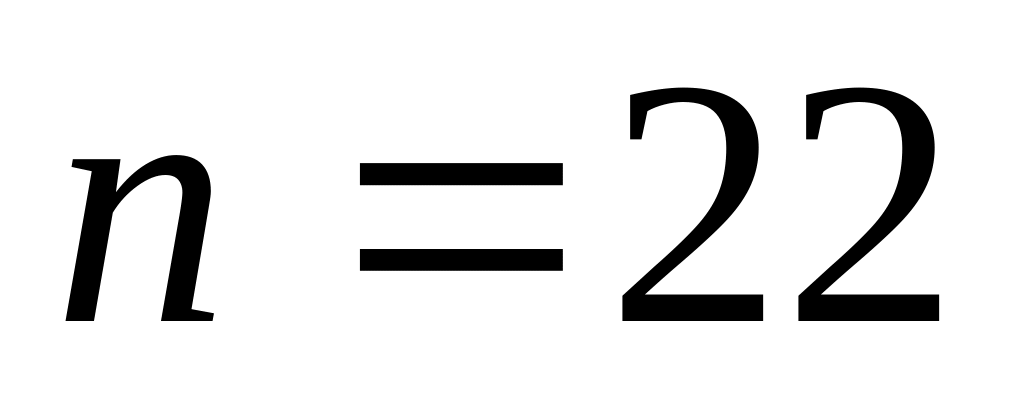• число определяемых пунктов ;

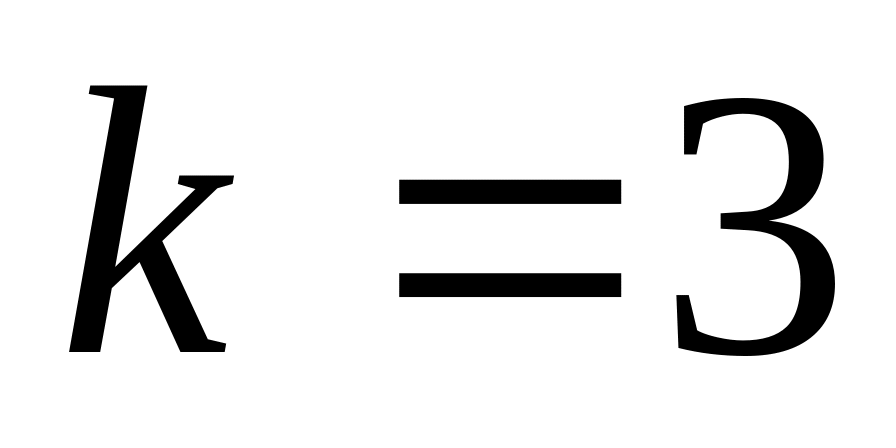• число исходных пунктов ;

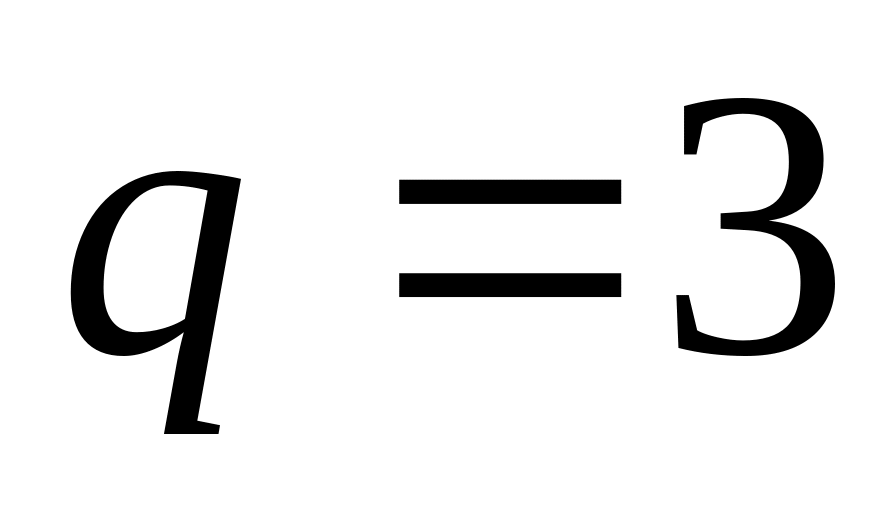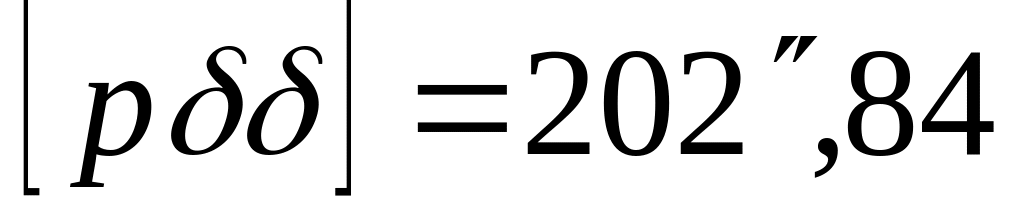• (см. табл. 3.12).

2. Определение средних квадратических ошибок координат определяемых пунктов.

Средние квадратические ошибки координат определяемых пунктов вычисляются по формуле:

;
.

3. При вставке одного пункта в триангуляционную сеть веса уравненных координат равны

;
,

где и – коэффициенты преобразованных уравнений поправок.

Подставив значения весов в выражения средних квадратических ошибок, получим:

.
.

Средняя ошибка положения вставляемого пункта вычисляется по формуле:

.

Дополнительная оценка точности при вставке одного пункта. Построение подеры.

Угол поворота вычисляется по формуле:

.

Четверть для определяется как при обычном вычислении дирекционного угла по прямоугольным координатам.

Величины максимального и минимального смещения положения пункта определяются по формулам:

;
;
;

Радиус-вектор подеры (педальной кривой) определяется по формуле:

,

где – некоторый угол поворота;

А – это максимальное и В – минимальное значения средней ошибки некоторого эллипса, который называется средним квадратическим эллипсом ошибок.

Подера может быть представлена как кривая, образованная непрерывным перемещением конца перпендикуляра, восстановленного из центра эллипса к касательной в некоторой точке эллипса при непрерывном изменении ее положения на эллипсе.

4. При вставке двух пунктов в триангуляционную сеть используются следующие формулы:

;
.
;
,
.
;
;
;
,

В рассматриваемых формулах величина вычисляется:

.

5. При вставке трех пунктов в триангуляционную сеть используются формулы:

;
.
;
,
.
;
;
;
,

В рассматриваемых формулах величина вычисляется:

6. Определение средней квадратической ошибки дирекционного угла стороны между вставляемыми пунктами. Для этого составляется весовая функция:

.

Зная коэффициенты весовой функции, в схеме Гаусса вычисляют в колонке u величину, равную обратному весу функции по формуле:

Средняя квадратическая ошибка дирекционного угла стороны равна:

6. Определим средние квадратические ошибки координат пункта Штейерндиб.

На основании расчетов, выполненных в таблице 3.11, имеем

;

Тогда

;
.

Веса уравненных координат равны:

;

Угол поворота

Величины максимального и минимального смещения положения определяемого пункта Штейерндиб

;
;
;
;

Вычисляем значения радиус-векторов подеры Р:

,

Таблица 3.15 – Вычисление радиус-векторов подеры на пункте Штейерндиб

, град
15	0,966	0,933	1,102	0,259	0,067	0,052	1,154	1,074
30	0,866	0,750	0,886	0,500	0,250	0,194	1,080	1,039
45	0,707	0,500	0,590	0,707	0,500	0,388	0,978	0,989
60	0,500	0,250	0,295	0,866	0,750	0,582	0,877	0,937
75	0,259	0,067	0,079	0,966	0,933	0,724	0,803	0,896
90	0,000	0,000	0,000	1,000	1,000	0,776	0,776	0,881

По полученным данным выполняем построение подеры (рис. 3.2).

Определим среднюю квадратическую ошибку дирекционного угла стороны Штейерндиб – Шанце. Составим весовую функцию:

.

Определяем коэффициенты весовой функции. Коэффициенты выписываем из табл. 3.6 для направления Штейерндиб – Шанце:

Подставив полученные коэффициенты в таблицу 3.11, получаем значения для вычисления величины, равной обратному весу функции по формуле:

;
;
;
;
.

Средняя квадратическая ошибка дирекционного угла стороны Штейерндиб – Шанце:

Рис. 3.2. – Построение подеры на пункте Штейерндиб

Масштаб подеры 1:2

Приложение А – Решение нормальных уравнений по схеме Гаусса-Дулитля (в общем виде)

								Порядок вычислений
								1
-1								2
								38
								3
								4
								5
	-1							6
								37
								7
								8
								9
								10
		-1						11

Продолжение приложения А

								36
								12
								13
								14
								15
								16
			-1					17
								35
								18
								19
								20
								21
								22
								23

Продолжение приложения А

				-1				24
								34
								25
								26
								27
								28
								29
								30
								31
					-1			32
								33
								39
								40

Продолжение приложения А

								41
								42
								43
								44
								45
								46