Роторная таблеточная машина (мт).

Рассматриваемый класс машин может иметь как жесткую, так и нежесткую программу и предназначены преимущественно для производства штучной продукции.

В машинах-автоматах III класса исполнительные органы машины выполняют операции технологического процесса на подвижном объекте обработки, причем непрерывное транспортное перемещение имеют и объект обработки, и исполнительные органы машины. Таким образом, ИО выполняют основные и вспомогательные операции при непрерывном транспортном движении ОО.

МА III класса многопозиционные, могут быть многопоточными, а исполнительные органы – многогнездными.

Рис. 4. Схема перемещения объекта обработки в машинах III класса (роторного типа)

Транспортное движение в этих машинах обычно происходит по круговой траектории (рис.4), соответственно их называют машинами роторного типа.

В рассматриваемых машинах объекты обработки при помощи загрузочных устройств устанавливаются в определенных позициях непрерывно вращающегося ротора. Позиции располагаются по окружности ротора с постоянным шагом. Центральный угол между осями соседних позиций ротора (угловой шаг)

где u – число позиций в роторе.

Машины этого класса выдают одно готовое изделие (или группу изделий, если позиции многогнездные) каждый раз, когда очередная позиция подходит к устройству съема изделий, т.е. при повороте ротора на угол a или при перемещении транспортера на величину шага. Поэтому рабочий цикл равен времени поворота ротора на угол a :

где w - угловая скорость ротора.

В роторной машине можно выполнить несколько операций.

Рабочий цикл машины можно выразить через время T_T , необходимое для осуществления основных и вспомогательных операций технологического цикла. Например, для роторной машины за время T_T ротор поворачивается на угол y , меньший 2p. В остальной части угла поворота ротора 2p - y осуществляется холостой ход или выполняются такие внецикловые операции, как контроль состояния инструмента, его замена и пр.

Обозначая через m и k соответственно число позиций ротора, в которых имеется и отсутствует воздействие ИО на ОО ( u = m + k ), получим для угла поворота ротора

y = a (m – 1) = w T_T ,

о ткуда следует

и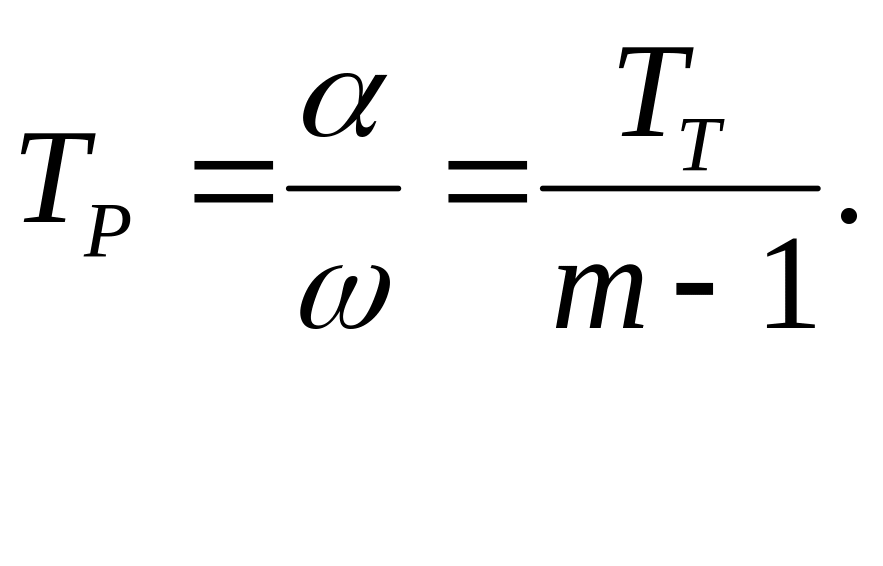

П оскольку m = u – k , получим

Из этой формулы следует, что в отличие от других машин рабочий цикл машин III класса при заданном Т_Т зависит от числа позиций u в роторе и уменьшается с увеличением их числа.

Технологический и кинематический цикл роторной машины определяются выражениями

T_T = T_P (u – k – 1),

T_K = T_P u.

Циклограмма рассматриваемых МА представляет собой совмещенные друг с другом циклограммы отдельных исполнительных механизмов за один оборот ротора.

α – угол между двумя позициями

u=12; К=2; m=10

Тр= α/ =2π/u

Тк=Тр*u

Q4=1/Тр

Q⁴>Q³>Q²>Q¹

Лекция №5

Производительность МА. Исполнительные механизмы

Исполнительные механизмы.

Классификация по конструктивному признаку

1. Шарнирно-рычажный механизм

2. Кулачковый механизм

3. Прерывисто-вращательного движения

4. Храповые механизмы

5. Гидравлический исполнительный механизм

6. Пневматический исполнительный механизм

Функции исполнительных механизмов в МА.

1. Кинематическая (перемещение, вращение и т. п.).

2. Энергетическая (силовая) функция.

3. Информационная.

Расчет времени срабатывания.

Время срабатывания – это время перемещения исполнительного механизма из одного положения в другое.

Совокупность кинематических и силовых функций каждого исполнительного механизма определяется характером материального и энергетического потоков в данной конкретной машине.

В одних случаях при этом возможно преобладание кинематических функций исполнительного механизма (обычно при выполнении вспомогательных операций), в других – силовых.

В некоторых машинах-автоматах исполнительные механизмы имеют кинематическую схему, обеспечивающую движение точек исполнительных органов по весьма сложным траекториям. Часто исполнительные органы имеют сравнительно простые траектории движения, например, отрезки прямой. Однако, при перемещении ИО по этим траекториям преодолеваются значительные технологические сопротивления. Например, в пресс-автомате для изготовления графитовых блоков при поступательном перемещении пуансона механизма прессования сила технологического сопротивления не постоянна и резко увеличивается в конце хода.

Как уже было отмечено, и кинематическая, и энергетическая (силовая) функции исполнительного механизма реализуются в соответствии с закодированной программой машины-автомата. Это проявляется, прежде всего, в цикличности его работы и согласованности действия данного механизма с действиями других исполнительных механизмов. Однако взаимодействие между исполнительными механизмами не ограничивается лишь необходимостью получения заданного чередования рабочих и вспомогательных операций, приходится определять и время перемещения отдельных элементов исполнительных механизмов на каких-то участках траектории их движения.

Время срабатывания исполнительного механизма – время, в течение которого происходит перемещение ИО механизма или какой-либо точки, ему принадлежащей, на заданном интервале пути.

Время срабатывания определяется экспериментально при наличии объекта исследования и расчетным путем - на стадии проектирования МА.

Расчетная методика нахождения времени срабатывания выбирается в зависимости от исходных данных.

Вариант 1. Известна зависимость перемещения точки ведомого звена исполнительного механизма от времени s = s(t); начальное и конечное положения точки определены значениями s₁ и s₂; необходимо найти время срабатывания t_21.

При задании функции s = s(t) в виде графика искомая величина представляет собой разность абсцисс: t₂₁ = t₂ – t₁.

Для аналитического решения необходимо найти обратную функцию- t(s). Тогда

t₂₁ = t(s₂) – t(s₁).

Вариант 2. Известна зависимость скорости точки ведомого звена исполнительного механизма от его положения: v = v(s), начальное и конечное положения точки s₁ и s₂. Определить время срабатывания t₂₁ .

Для решения задачи используется соотношение

о ткуда

и

Вариант 3. Заданы зависимость движущей силы от перемещения P_Д = P_Д(s) и сил сопротивления P_С = P_С(s); зависимость приведенной массы механизма от его положения m_П = m_П(s), начальная скорость v₁, начальное и конечное положения механизма s₁ и s₂ , Определить время срабатывания t₂₁.

В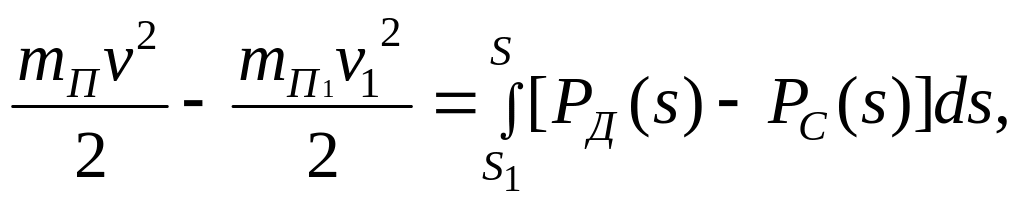 данной постановке задача решается с использованием уравнений динамики машин, например, в форме закона изменения кинетической энергии

с ледовательно

Зная теперь зависимость v(s) переходим к решению задачи по варианту 2.

Рассмотрим в качестве примера определение времени срабатывания двухзвенного механизма (рис. 2. 2) с приводом от пружины. Подобного рода механизмы в сочетании с другими применяются в машинах автоматах как транспортные, фиксирующие и т.п. Эти механизмы выполняют вспомогательные, а в некоторых случаях и рабочие операции.

Принимается, что в начальном положении пружина сжата и на ведомое звено 2 со стороны пружины 1 действует сила P_max, закон изменения которой задан графиком P(s). Сила сопротивления Q, приложенная к ведомому звену, принимается постоянной и известной по величине; масса звена - m; S_max - полная деформация пружины, ход звена – S₂ . Масса пружины не учитывается.

Рис. 2. 2 Схема пружинного механизма

Определим величину движущей силы пружины P, действующей на ведомое звено 2 в положении, когда оно находится на расстоянии s от левого крайнего положения.

И з диаграммы пружины следует

откуда

В начальный момент v₁ = 0 (звено неподвижно); в соответствии с вариантом 3 получим

И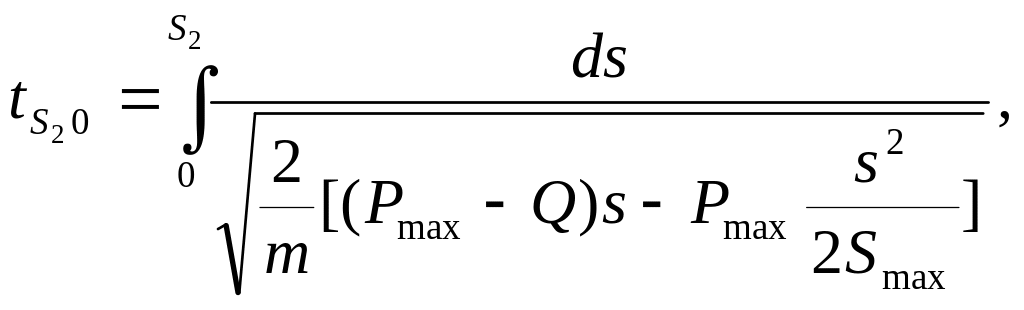 спользуя 2-ой вариант решения, найдем

и после интегрирования

В частном случае, если силы сопротивления отсутствуют (или если ими можно пренебречь), т.е. при Q=0,

Для расчета времени срабатывания исполнительных механизмов и времени пуска машинного агрегата можно использовать ПК. Соответствующие программы (файл srabat99.exе и pusk_98.exe) были созданы на кафедре «Автоматизированное конструирование машин и аппаратов» МГУ ИЭ .

ТЕХНОЛОГИЧЕСКАЯ И ЦИКЛОВАЯ ПРОИЗВОДИТЕЛЬНОСТЬ

Главная задача теории производительности машин – выявление и анализ влияния структурных, конструктивных и эксплуатационных факторов на производительность рабочих машин.

Прикладная задача теории производительности заключается в решении вопроса расчета, проектирования и эксплуатации рабочих машин, и в том числе машин-автоматов, исходя из обеспечения высокой производительности и эффективности вновь создаваемой техники.

Большинство машин-автоматов имеют рабочий цикл Т_р, в который, помимо времени выполнения рабочих ходов t_р = t_pi , входит и время холостых перемещений рабочих органов t_x = t_xi и, следовательно,

Т_р = t_р + t_x. Основа для создания любой рабочей машины – технологический процесс, выполняемый машиной. Исследование технологического процесса и его элементов – первичных операций позволяет установить оптимальные параметры режима их выполнения: время, скорость, усилие, температуру и т.п. Таким образом можно определить общую затрату времени, необходимую для выполнения всех основных операций обработки и, следовательно, найти технологическую производительность машины Q_тхл, которая представляет собой количество изделий, изготовляемых в единицу времени при отсутствии холостых ходов:

Цикловая производительность (или теоретическая производительность) машины-автомата определяется количеством изделий, выдаваемых машиной в единицу времени в предположении, что машина работает непрерывно и вся ею производимая продукция удовлетворяет техническим требованиям, предъявляемым к ее качеству.

Е сли за рабочий цикл Т_р с в одном потоке выдается одно изделие, а общее число потоков (или гнезд в позициях) w, то цикловая производительность машины шт/с будет

Время Т_р зависит от структуры машины. Для нескольких типов машин  и  классов, выпускающих штучную продукцию, в табл. 4. 1. приведены формулы расчета времени рабочего цикла Т_р (см. гл. 3) и цикловой производительности Q_ц.

Таблица