Расчет времени срабатывания гидроцилиндра двойного действия.

В машинах-автоматах под временем срабатывания гидравлического исполнительного механизма понимается время перемещения поршня и соединенного с ним рабочего органа машины из одного крайнего положения в другое.

Предполагается, что давление в напорной линии перед распределителем Р (см. рис. 9. 1) постоянное.

Отсчет времени срабатывания t_С ведется с момента переключения распределителя Р. В общем случае в состав времени срабатывания входят следующие элементы

1.Время t_РАС распространения упругой волны (давления) в жидкости, находящейся втрубопроводе, соединяющим распределитель с гидроцилиндром ГЦ. Это время рассчитывается по скорости с распространения звука в рабочей жидкости:

t_РАС= L /c,

где L – длина участка трубопровода между распределителем и гидроцилиндром. Для воды и минеральных масел при условиях эксплуатации гидроприводов с  1430 м/с. Время t_РАС очень незначительно, его в расчетах обычно не учитывают.

2 Время t_У ускоренного движения поршня. Как показывает опыт эксплуатации гидропривода, эта составляющая, как правило, мала, однако, в каждом конкретном случае необходим анализ величины ее вклада.

3 .Время t_Р равномерного движения поршня – основная составляющая времени срабатывания.

4.Время t_Т торможения поршня. При отсутствии тормозных устройств t_Т = 0, а при их наличии t_Т подлежит поверочному или проектному расчету.

Таким образом

t_С = t_РАС + t_У + t_Р + t_Т .

При выполнении предпроектного синтеза машины-автомата грубая оценка времени срабатывания гидравлического исполнительного механизма осуществляется только с учетом времени t_Р и t_Т . Если известны полный ход S поршня, его перемещение при торможении S_T, скорость v_P равномерного движения и время t_Т торможения, то

t_С = (S  S_T)/ v_P+ t_Т.

Анализ движения поршня. Длительности интервалов t_У , t_Р , t_Т можно найти интегрированием дифференциального уравнения движения поршня гидравлического цилиндра.

При составлении этого уравнения вводятся следующие допущения:

Масса движущихся частей, включая и массу жидкости в трубах и цилиндре, остается в процессе движения поршня постоянной.

2. Давление р₁ в напорной линии, а также р₂ в линии слива при работе механизма не меняются .

Сила Р_С технологического сопротивления, приложенная к штоку поршня постоянна или может быть приведена к постоянной на отдельных участках его перемещения.
Силы трения в уплотнения в подвижных соединениях от скорости движения поршня не зависят.
Упругие деформации рабочей жидкости не учитываются.
Температура рабочей жидкости в процессе движения поршня не меняется.
Геометрический напор по сравнению с пьезометрическим мал и им можно пренебречь.
Потоки жидкости – неразрывные, режим движения жидкости в трубах – ламинарный.

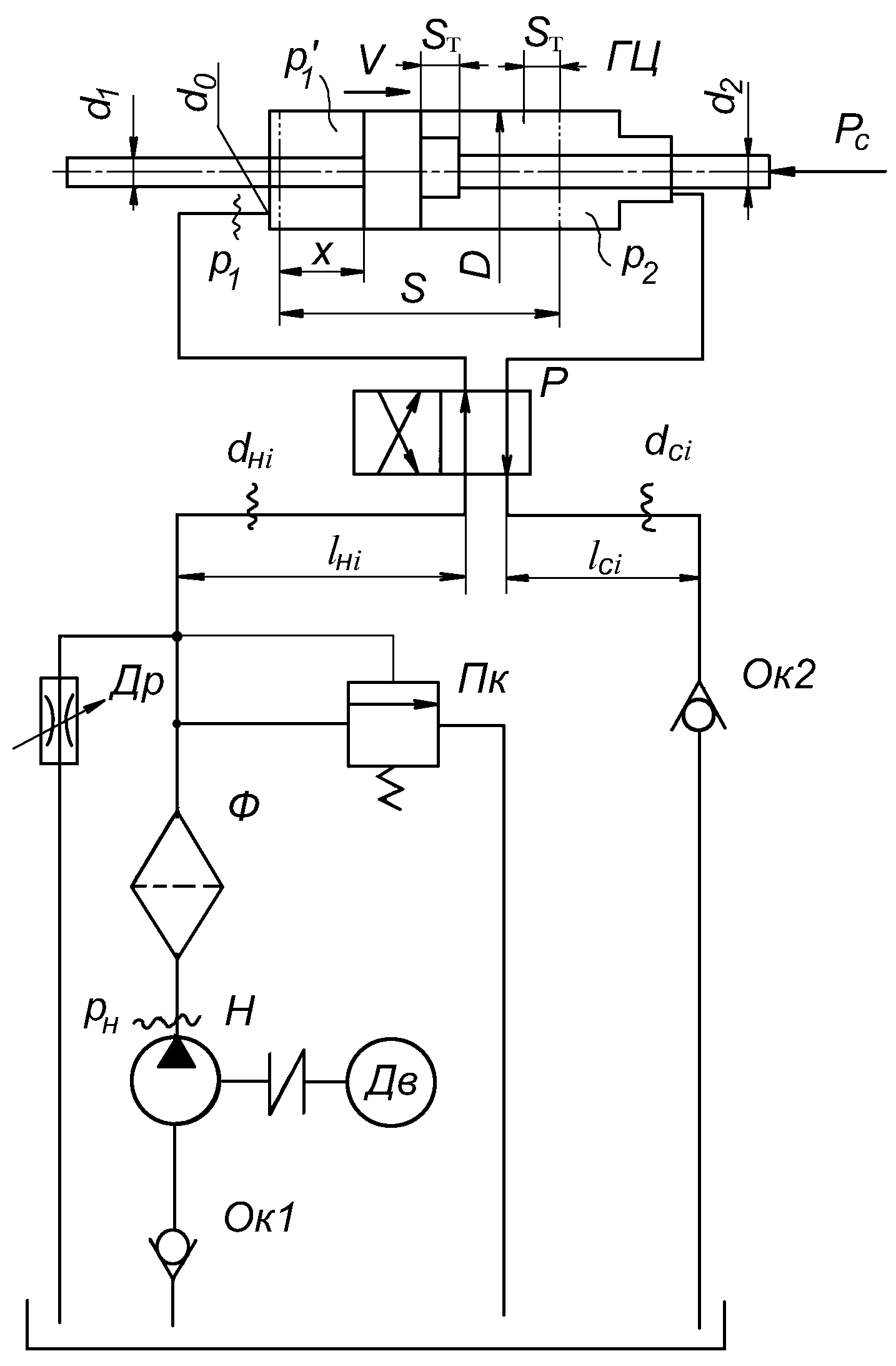
Рис12.. Гидравлическая схема к расчету времени срабатывания:

ГЦ – гидроцилиндр; Р – распредеделитель; Др – дроссель регулируемый; Пк – клапан переливной; Ф – фильтр; Н – насос; Дв – двигатель; ОК1, ОК2 – клапаны обратные

На основании второго закона Ньютона дифференциальное уравнения движения поршня для гидроцилиндра с односторонним штоком (рис) можно записать в виде

m^ dv/dt = p₁ F₁ – p₂ F₂ – P_С ,

где m^  приведенная к поршню масса движущихся частей;

p₁  давление рабочей жидкости в бесштоковой полости поршня;

F₁– площадь живого сечения цилиндра слева [для бесштоковой полости - D² /4; при наличии штока - (D² – d₁² )/4];

F₂ площадь живого сечения цилиндра справа - (D² – d₁² )/4.

П риведенная масса m^ складывается из массы соединенных с поршнем поступательно движущихся частей и массы жидкости, заполняющей нагнетательную и сливную линии трубопроводов. Для расчета ее величины используется условие равенства кинетической энергии приведенной массы и упомянутых реальных масс

В этом выражении m_П  масса всех поступательно движущихся частей, соединенных со штоком.

Принимая во внимание, что отношение скорости v_i жидкости в i  ом трубопроводе к скорости v поршня обратно пропорционально площадям их сечений, получим

m^ = m_П +  m_i (D/d_i )⁴.

Масса жидкости в i – ом участке трубопровода, имеющего диаметр d_i и длину l_i , равна

m_i =  l_i d_i ²/4,

где   плотность рабочей жидкости.

Д авление p₁ в бесштоковой полости гидроцилиндра определяется с помощью уравнения Бернулли для расхода жидкости через отверстие диаметром d_o с коэффициентом расхода  (для круглых и квадратных отверстий   0,62) :