5

Міністерство освіти і науки, молоді та спорту України

Полтавський національний технічний університет

імені Юрія Кондратюка

Матеріал

до виконання розрахунково-графічної роботи з курсу

“Основи метрології, стандартизація та контроль якості”

для студентів денної форми навчання

Розглянуто на засіданні кафедри технології машинобудування,

протокол № 6 від 22 лютого 2012 p.

Завідувач кафедри професор М.Д. Жолткевич

Укладач доцент С.М. Гнітько

Полтава 2012 р.

Методичні вказівки до виконання курсової роботи з курсу “Основи метрології, стандартизація та контроль якості” для студентів денної форми навчання/ Уклад. канд. техн. наук, доцент С.М. Гнітько ‑ Полтава: ПНТУ, 2012.

З міст

Стор.

Вступ 3

Задача 1. Визначення допусків

гладких циліндричних з’єднань 3

Задача 2. Визначення виконавчих

розмірів та допусків гладких граничних калібрів 9

Задача 3. Визначення допусків поверхонь на

посадку для підшипника кочення 15

Задача 4. Розрахунок розмірного ланцюга при забезпеченні точності вихідної ланки 23

Задача 5. Визначення допусків різьбового

з’єднання 31

Задача 6. Встановлення числових значень допусків зубчастої передачі 35

Задача 7. Визначення допусків шліцьового

з’єднання 45

Задача 8. Визначення допусків шпонкового

з’єднання 50

Список рекомендованої літератури 53

Вступ

Мета виконання розрахунково-графічної роботи при вивченні курсу "Основи метрології, стандартизація та контроль якості" ‑ закріпити теоретичні знання, а також розвинути у студентів практичні навики застосування допусків і посадок згідно з їх призначенням.

У розрахунково-графічній роботі студенти вирішують задачі, дані для яких вказані у кожному прикладі виконання завдання.

Номер завдання приймається відповідно двом останнім цифрам номера залікової книжки, вихідні дані коригуються викладачем.

Розрахунково-графічну роботу представляють на кафедру технології машинобудування у вигляді пояснювальної записки.

Пояснювальну записку виконують на листах паперу розмірами 210297 мм прописом на одному боці аркуша і вставляють у загальну обкладинку.

Усі рисунки, виконані у пояснювальній записці у вигляді ескізів виносяться на креслення. Вони мають бути виконані з необхідним дотримуванням масштабу зображення. Обов’язковим є складання програми на ПЕОМ будь-якої задачі або частини задачі, з поміщенням у записку курсової роботи лістингу даної програми та результатів розрахунку.

При погодженні з викладачем дозволяється курсову роботу виконувати на комп’ютері.

Задача №1. Визначення допусків гладких циліндричних з’єднань

Завдання: Для трьох циліндричних з’єднань: з зазором, з натягом, по перехідній посадці (табл.1.1) треба:

1. визначити допуски розмірів отвору та валу;

2. зобразити схеми полів допусків отвору та валу;

3. проставити на рисунках з’єднання позначення посадок згідно з ЕСКД;

4. для перехідної посадки визначити найбільш імовірні величини зазорів і натягів та вирахувати відсоток з’єднань з натягом.

Приклад виконання завдання, сполучення 63 Н8/n7

1. З’єднання 63Н8/n7 виконано у системі отвору. Відхилення отвору 63Н8 (основний отвір) за 8 квалітетом, вала 63n7 за 7 квалітетом.

2. За таблицею СТ СЭВ 144-75 обирають граничні відхилення: для отвору H8 з номінальним розміром 63 мм [1, с.118]:

а) верхнє граничне відхилення ЕS = +46 мкм = + 0,046 мм;

б) нижнє граничне відхилення EI=0;

Для вала n7 з номінальним розміром 63 мм [1, с.91]:

а/верхнє граничне відхилення ES = +50 мкм = 0,05 мм;

б/нижнє граничне відхилення EI = +20 мкм = 0,02 мм.

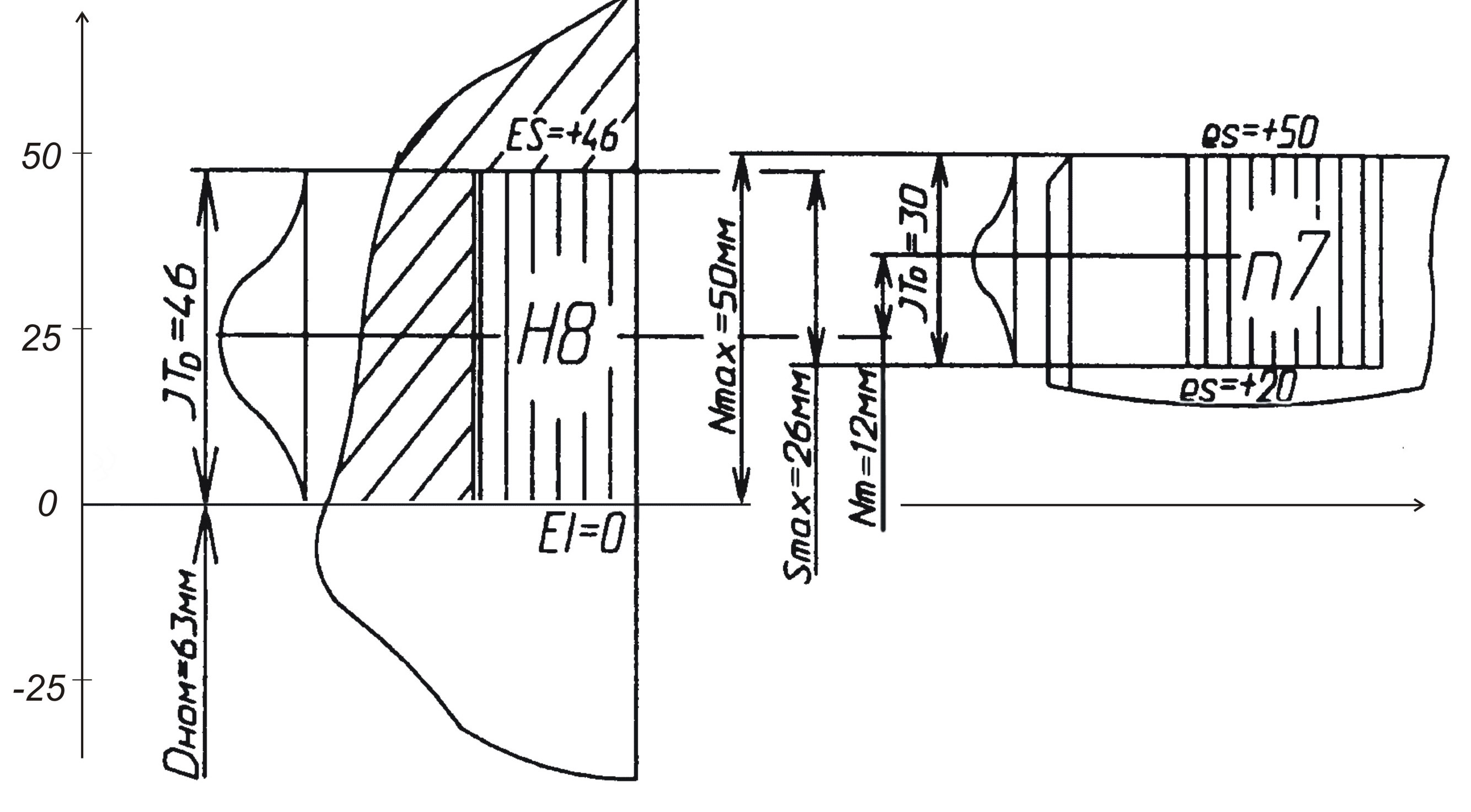3. Графічне зображення полів допусків з’єднання (рис. 1.1).

Р исунок 1.1 ‑ Розташування полів допусків розмірів отвору та вала для з’єднання 63Н8/n7 з графіками розсіювання імовірних розмірів отвору та вала

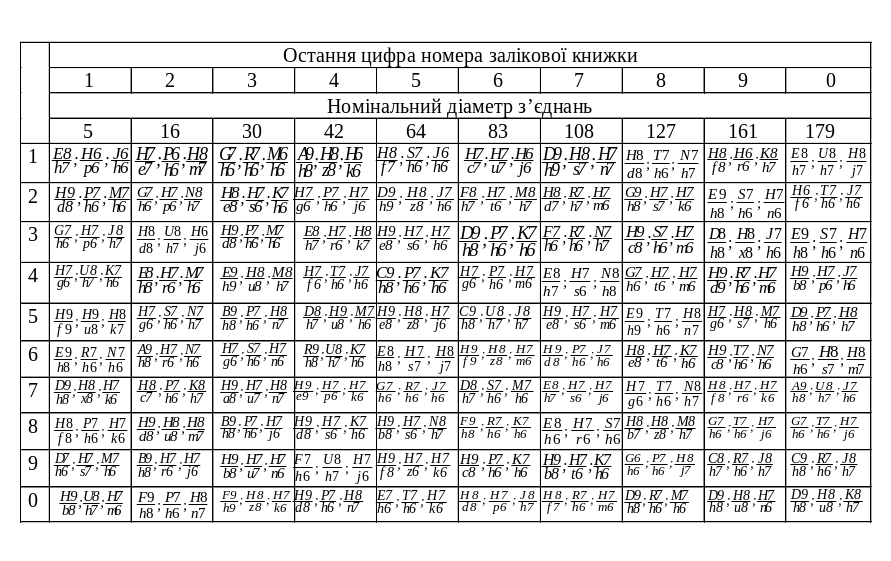
Таблиця 1.1 ‑ Вихідні дані до задач 1,2 "Визначення допусків

циліндричних з‘єднань", та „Визначення виконавчих розмірів та допусків гладких граничних калібрів”

4. Допуски отвору та вала: TD = ES - EI= 46 - 0 = 46 мкм.

Td = es - ei = 50 - 20 = 30мкм.

5. Найбільший зазор: S _max= ES - ei = 46 - 20 = 26 мкм.

Найбільший натяг: N _mах= EI - es = 50 - 0 = 50 мкм.

Середній натяг:

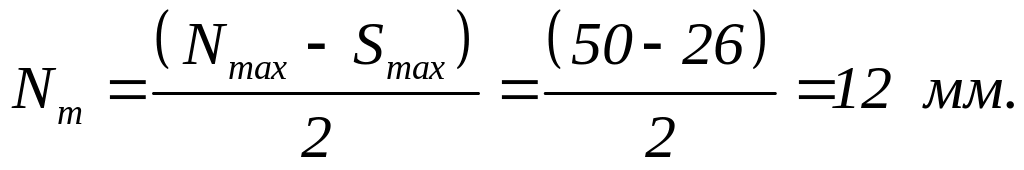
6. Допуск посадки: T_p = TD + Td = 46 + 30 = 76 мкм.

Таблиця 1.2 ‑ Результати розрахунків сполучень

	Допуск, мкм		Зазор, мкм			Натяг, мкм			Допуск
З’єднан­ня	отвір	вал	най- біль-ший	се-ред-ній	най-мен­ший	най- біль-ший	се­ред­ній	най­мен­ший	посадки, мкм
63 Н8/n7	46	30	26	‑	‑	50	12	‑	76
Позна­чення	TD	Td	Smax	Sm	Smin	Nmax	Nm	Nmin	Tp

7. (Виконується тільки для перехідного сполучення) В перехідних посадках ступінь легкості складання та розбирання визначають імовірністю одержання у них зазорів чи натягів, (вираховують кількість з’єднань з натягом у відсотках від загальної кількості з’єднань).

Можна очікувати, що розподіл випадкових величин відхилень розмірів отвору та валу підпорядковується функції нормального розподілу (закону Гауса ). Визначимо з довірчою імовірністю +3 середнє квадратичне відхилення функції нормального розподілу для отвору та вала:

_D = = 7,7 мкм, _d = = 5 мкм.

Середнє квадратичне відхилення допуску посадки _N визначаємо за формулою теорії імовірності:

мкм.

Центр групування кривої розподілу зазорів - натягів збігається з лінією середнього натягу, тобто відповідає найбільш ймовірним розмірам отвору та валу: М_(х) = N_c = 12 мкм.

Визначимо значення координати довірчого інтервалу розмірності середнє квадратичного відхилення _N, який відповідає межі натягів та зазорів на графіку розсіювання зазорів (рис. 1.2):

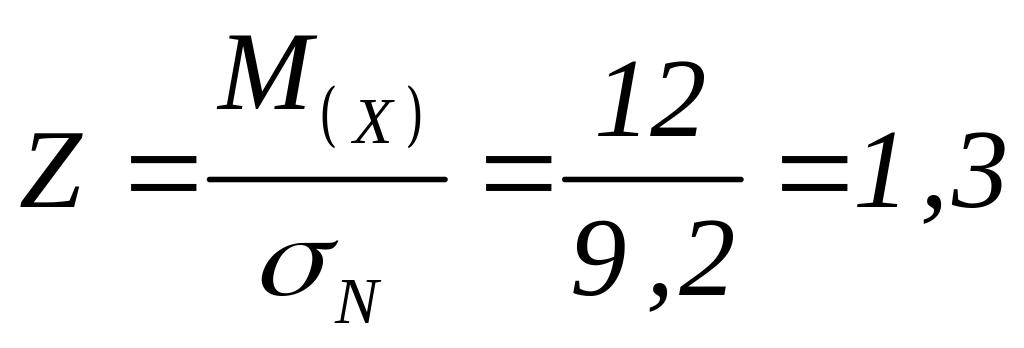
За табл. 1.3 знаходимо Ф (1,3) = 0,403.

Т.ч., відносна кількість з’єднань з натягом буде 0,5 + 0,403 = = 0,903 або 90,3%, з’єднань із зазором відповідно 9,7%.

-18,4

T_p

-27,6

-9,2

9,2

+18,4

+27,6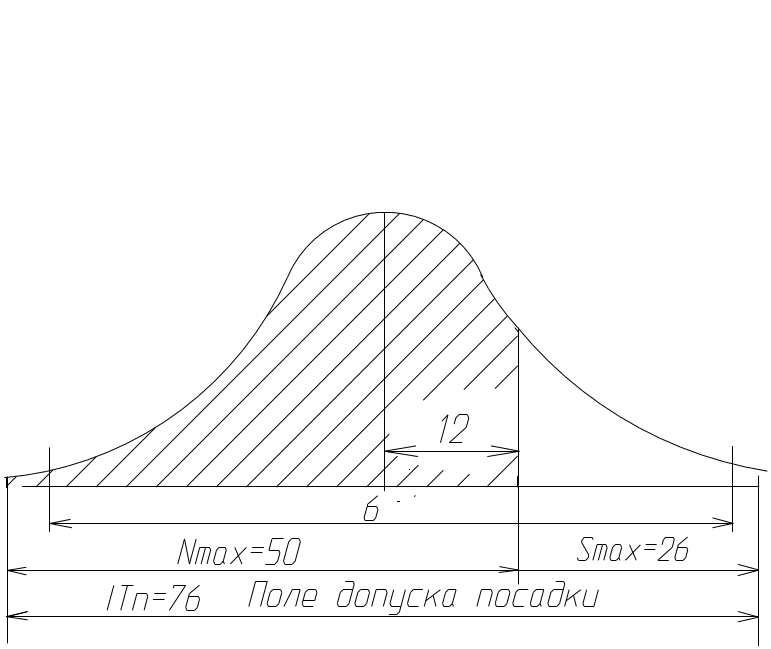

Рисунок 1.2 ‑ Графік розсіювання зазорів та натягів

з’єднання 63 H8/n7

Таблиця 1.3 ‑ Значення функцій Ф(t)

інтеграла ймовірностей (інтеграла Лапласа) в межах від 0 до + 

	t, соті долі
t, цілі та десяті долі	0	1	2	3	4	5	6	7	8	9
0.0	0.000	0.004	0.008	0.012	0.016	0.019	0.023	0.027	0.031	0.035
0.1	0.039	0.043	0.047	0.051	0.055	0.059	0.063	0.067	0.071	0.075
0.2	0.079	0.083	0.087	0.090	0.094	0.098	0.102	0.106	0.110	0.114
0.3	0.117	0.121	0.125	0.129	0.133	0.136	0.140	0.144	0.148	0.151
0.4	0.155	0.159	0.162	0.166	0.170	0.173	0.177	0.180	0.184	0.187
0.5	0.191	0.195	0.198	0.201	0.204	0.208	0.212	0.215	0.219	0.222
0.6	0.225	0.229	0.232	0.235	0.238	0.242	0.245	0.248	0.251	0.254
0.7	0.258	0.261	0.264	0.267	0.270	0.273	0.276	0.279	0.282	0.285
0.8	0.288	0.291	0.293	0.296	0.299	0.302	0.305	0.307	0.310	0.313
0.9	0.315	0.318	0.321	0.323	0.326	0.328	0.331	0.334	0.336	0.338
1.0	0.341	0.343	0.346	0.348	0.350	0.353	0.355	0.357	0.369	0.362
1.1	0.364	0.366	0.368	0.370	0.372	0.374	0.377	0.379	0.381	0.383
1.2	0.384	0.386	0.388	0.390	0.392	0.394	0.396	0.398	0.399	0.401
1.3	0.403	0.404	0.406	0.408	0.409	0.411	0.413	0.414	0.416	0.417
1.4	0.419	0.420	0.422	0.423	0.425	0.426	0.427	0.429	0.430	0.431
1.5	0.433	0.434	0.435	0.437	0.438	0.439	0.440	0.441	0.442	0.444
1.6	0.445	0.446	0.447	0.448	0.449	0.450	0.451	0.452	0.453	0.454
1.7	0.455	0.456	0.457	0.458	0.459	0.459	0.460	0.461	0.462	0.463
1.8	0.464	0.464	0.465	0.466	0.467	0.468	0.469	0.469	0.469	0.470
1.9	0.471	0.471	0.472	0.473	0.474	0.474	0.475	0.475	0.476	0.476
2.0	0.477	0.477	0.478	0.478	0.479	0.479	0.480	0.480	0.481	0.481
2.1	0.482	0.482	0.483	0.483	0.483	0.484	0.484	0.485	0.485	0.485
2.2	0.486	0.486	0.486	0.487	0.487	0.487	.0488	0.488	0.488	0.489
2.3	0.489	0.489	0.489	0.490	0.490	0.490	0.490	0.491	0.491	0.491
2.4	0.491	0.492	0.492	0.492	0.492	0.492	0.493	0.493	0.493	0.493
2.5	0.493	0.494	0.494	0.494	0.494	0.494	0.494	0.494	0.495	0.495
2.6	0.495	0.495	0.495	0.495	0.495	0.496	0.496	0.496	0.496	0.496
2.7	0.496	0.496	0.496	0.496	0.496	0.497	0.497	0.497	0.497	0.497
2.8	0.497	0.497	0.497	0.497	0.497	0.497	0.497	0.497	0.498	0.498
2.9	0.498	0.498	0.498	0.498	0.498	0.498	0.498	0.498	0.498	0.498
3.0	0.498	0.498	0.498	0.498	0.498	0.498	0.498	0.498	0.499	0.499
3.1	0.499	0.499	0.499	0.499	0.499	0.499	0.499	0.499	0.499	0.499
3.2	0.499	0.499	0.499	0.499	0.499	0.499	0.499	0.499	0.499	0.499
3.3	0.499	0.499	0.499	0.499	0.499	0.499	0.499	0.499	0.499	0.499
3.4	0.499	0.499	0.499	0.499	0.499	0.499	0.499	0.499	0.499	0.499