
- •Содержание
- •Условные сокращения
- •Условные обозначения
- •Предисловие
- •Часть 1 основы метрологии глава 1 основные понятия и определения
- •1 Измерения необходимы для получения информации о свойствах объектов, процессов, явлений;
- •2 Измерительная информация представляется в виде количественных оценок тех или иных физических величин, отражающих свойства объектов;
- •3 Достоверность измерительной информации определяется погрешностью измерений.
- •Глава 2 виды измерений
- •Глава 3 средства измерений
- •3.1 Виды средств измерений
- •3.2 Метрологические характеристики средств измерений
- •3.3 Классы точности средств измерений
- •Глава 4 методы измерений
- •Глава 5 похибки вимірювань
- •5.1 Виды погрешностей и их описание
- •5.2 Источники погрешности измерений
- •5.3 Оценка погрешности при прямых измерениях
- •5.4 Оценка погрешности при косвенных измерениях
- •5.5 Способы достижения требуемой точности
- •5.5.1 Способы уменьшения постоянной систематической погрешности
- •5.5.2 Уменьшение случайной погрешности
- •5.6 Запись результатов измерений
- •Глава 6 обеспечение единства измерений
- •Часть 2 техника измерений электрических величин в электронике глава 7 общие требования к измерениям
- •Глава 8 техника измерений параметров электрических цепей
- •8.1 Общие сведения о радиоэлектронных цепях
- •8.2 Измерительные генераторы
- •8.2.1 Назначение и номенклатура измерительных генераторов
- •8.2.2 Структурные схемы и особенности построения генераторов
- •8.2.3 Особенности выходных цепей
- •8.3 Средства и способы измерения параметров цепей с сосредоточенными постоянными
- •8.3.1 Средства и способы измерения параметров двухполюсных цепей
- •8.3.1.1 Параметры линейных компонентов цепей с сосредоточенными постоянными
- •8.3.1.2 Средства измерений параметров линейных двухполюсников
- •8.3.1.3 Способы подключения двухполюсников к измерительной схеме
- •8.3.2 Средства и способы измерения параметров четырехполюсных цепей
- •8.3.2.1 Основные параметры линейных четырехполюсников
- •8.4 Аппаратура и способы измерений параметров цепей с распределенными постоянными
- •8.4.1 Параметры цепей с распределенными постоянными
- •8.4.2 Номенклатура средств измерений для измерений параметров цепей свч
- •8.4.3 Способы измерений параметров цепей свч
- •Глава 9 техника измерений параметров электрических сигналов
- •9.1 Параметры периодических электрических сигналов
- •9.2 Исследование сигналов во временной области при помощи осциллографов
- •9.2.1 Виды осциллографов
- •9.2.2 Структура и принцип действия осциллографа
- •9.2.3 Технические и метрологические характеристики универсального осциллографа
- •9.2.4 Осциллографические измерения
- •9.2.5 Техника осциллографирования сигналов
- •9.3 Исследование сигналов в частотной области
- •9.3.1 Общие сведения о спектре сигналов
- •9.3.2 Виды анализаторов спектра
- •9.3.3 Метрологические характеристики ас
- •9.3.4 Селективные вольтметры
- •9.3.5 Измерители нелинейных искажений
- •9.4 Техника измерений электрического напряжения
- •9.4.1 Виды вольтметров
- •9.4.2 Техника измерений постоянного напряжения
- •9.4.3 Общая характеристика вольтметров переменного напряжения
- •9.4 Техника измерений частоты сигналов
- •9.4.1 Способы измерений частоты
- •9.4.2 Способ дискретного счета
- •9.4.3 Гетеродинный способ измерения частоты
- •Заключение
- •Приложение a Значение коэффициента tq для случайной величины, имеющей распределение Стьюдента с n - 1 степенями свободы
- •Приложение б
- •Приложение в
- •Перечень ссылок
- •Основы метрологии и техника измерений
5.2 Источники погрешности измерений
Анализируя процесс измерений можно выделить четыре возможных источника возникновения погрешностей (рис. 5.3):
− свойства объекта измерений;
− свойства окружающей среды;
− квалификацию и состояние оператора, выполняющего измерение (или программное обеспечение контроллера автоматизированной установки или системы);
− свойства применяемого средства измерений.
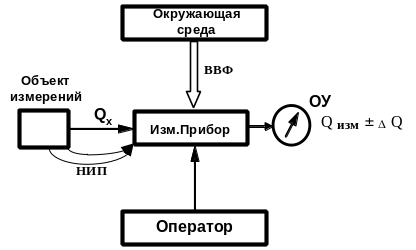
Qx – измеряемый (информативный) параметр; НИП – неинформативные параметры объекта измерений; ВВФ – внешние влияющие факторы окружающей среды; ОУ – отсчетное устройство.
Рисунок 5.3 Источники погрешности измерений
Как уже отмечалось, любой объект измерений характеризуется множеством физических величин. Из этого множества оператор выбирает физическую величину, подлежащую измерению – информативный параметр.
Множество других физических величин, не измеряемых в данном эксперименте, называют неинформативными параметрами объекта измерений. Эти неинформативные параметры объекта могут оказывать влияние на средство измерений и вызывать погрешности измерений. Так, при измерении действующего напряжения электрических сигналов на показания вольтметра переменного напряжения оказывают влияние следующие неинформативные параметры источника сигнала: частота сигнала, форма сигнала, выходное сопротивление источника сигнала. При измерении диаметра цилиндрической детали на показания микрометра оказывают влияние такие неинформативные параметры детали как температура детали, её некруглость и нецилиндричность.
Окружающая среда (условия выполнения измерений) также характеризуется набором физических величин (температура, напряженность электромагнитного поля, нестабильность напряжения питающей сети и т.п.), каждая из которых может оказывать влияние на средство измерений и вызывать погрешности измерений. Такие физические величины называют внешними влияющими факторами.
Технические характеристики средств измерений, отражающие свойства средств измерений и оказывающие влияние на результаты и на погрешности измерений, называются метрологическими характеристиками. Они достаточно подробно рассмотрены в подразделе 3.2.
Оператор, выполняющий измерение, также обладает свойствами, влияющими на погрешность измерений. Прежде всего, это его квалификация (неполное соответствие модели объекта измерений реальному объекту; неполное понимание физической природы измеряемой величины; неполное знание влияния условий окружающей среды на измерение; несовершенная оценка влияющих параметров окружающей среды), а также психофизическое состояние (внимательность, сосредоточенность, быстрота реакции, состояние зрения и нервной системы). Иногда оператор сознательно может искажать результат измерений с целью сокрытия брака в своей работе.
Погрешность оператора чаще встречается при большой доле ручного труда при проведении измерений и почти отсутствуют при использовании автоматизированных средств измерений.
5.3 Оценка погрешности при прямых измерениях
В методах обработки данных при прямых измерениях можно условно выделить две группы операций:
−формальные математические методы (обычно статистические);
−специфические метрологические операции.
Некоторые задачи обработки результатов измерения не могут быть формализованы, поэтому они решаются волевым путем, в соответствии с нормативно−техническими документами (НТД) по методам обработки данных. НТД разработаны специалистами в области метрологии с целью установления единообразия обработки данных при измерениях.
В этих НТД регламентируется решение неформализованных, неподдающихся строгому решению задач. Эти задачи, главным образом, связаны с анализом, оценкой и суммированием систематических погрешностей при прямых измерениях с однократными наблюдениями. Такие измерения широко распространены на производстве и в научных исследованиях.
Прямые измерения с однократными наблюдениями
Решение задачи по оценке погрешности при прямых однократных измерениях методом непосредственной оценки основано на взаимосвязи погрешности результата измерений и свойств применяемого измерительного прибора с учетом значений внешних влияющих факторов, отражающих условия применения прибора и с учетом значений неинформативных параметров объекта измерений, обуславливающих режим работы прибора (рис. 5.4). В качестве результата измерения принимают результат единичного считывания показаний прибора.
Погрешность результата определяется оценкой и суммированием следующих составляющих:
−основной погрешности измерительного прибора − Δосн;
−дополнительных погрешностей от внешних влияющих факторов (ВВФ) и от неинформативных параметров объекта измерений (НИПОИ) – Δдоп i;
−погрешности взаимодействия измерительного прибора и объекта измерений – Δвз;
−динамической погрешности – Δдин;
−вариации показаний измерительного прибора − Δвар (рис. 5.5).
Пределы допускаемой основной погрешности заимствуют из документации на измерительный прибор. Здесь необходимо обратить внимание на форму записи основной погрешности − абсолютная, относительная, приведенная. Если погрешность задана в абсолютной форме, ее выписывают из документации в той же форме. Если погрешность задана в относительной форме, то основная погрешность в абсолютной форме определяется по выражению:
Δ
≤ ±
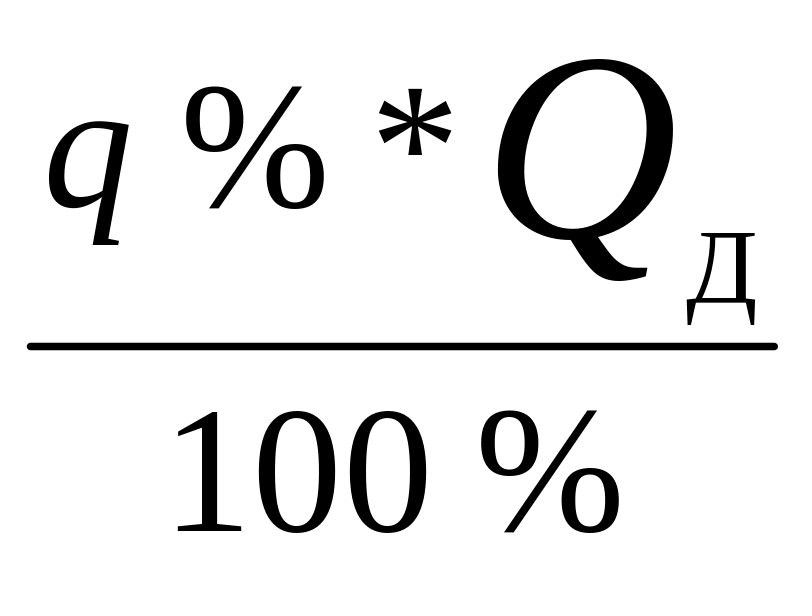 ,
,
где QД – действительное значение измеряемой величины (показание прибора).
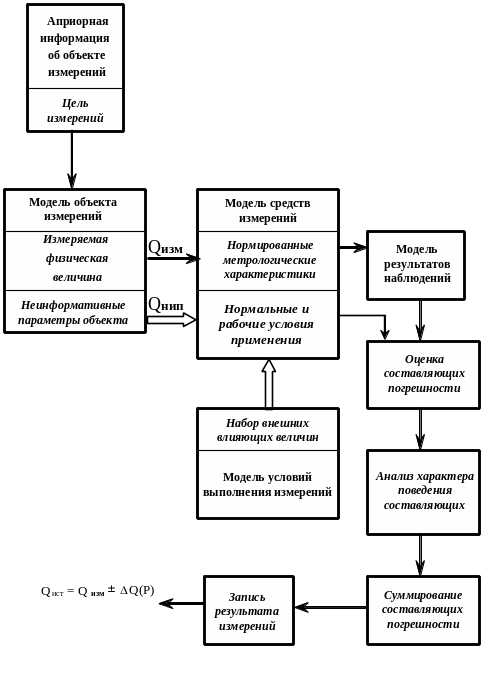
Рисунок 5.4 – Основные элементы процесса определения погрешности при прямых однократных измерениях
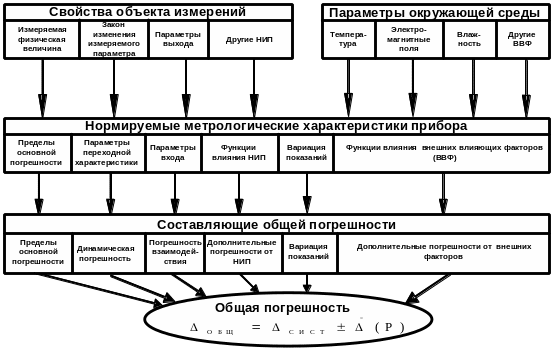
Рисунок 5.5 − Схема оценки погрешности прямых измерений
Если основная погрешность задана в приведенной форме, то основная погрешность в абсолютной форме определяется по выражению:
Δ
≤ ±
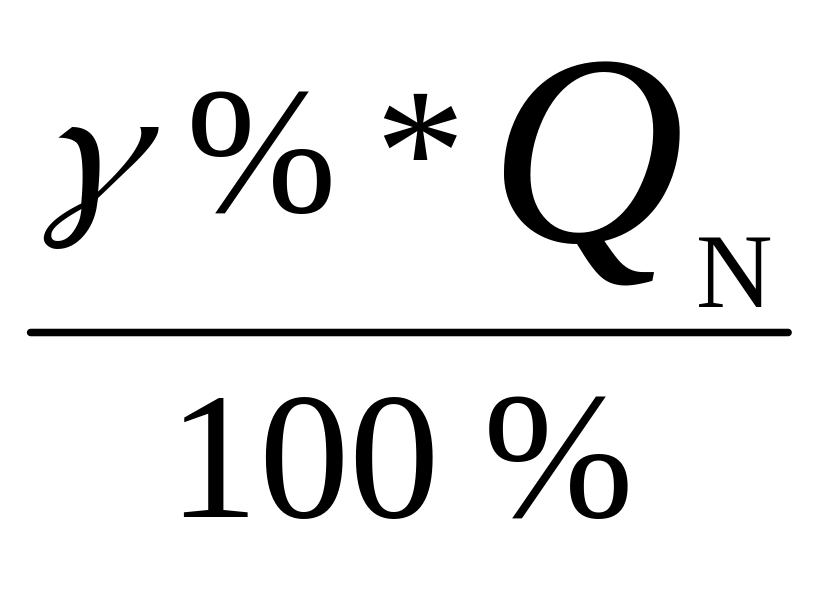 ,
,
где QN − нормирующее значение (чаще всего − конечное значение установленного поддиапазона).
Каждую из дополнительных погрешностей находят на основе оценок значений влияющих величин, соответствующих рабочим условиям применения прибора (чаще всего в виде границ − нижней и верхней), и подстановкой этих значений в функции влияния, которые также берут из документации на измерительный прибор, т.е.
Δдоп
i ≤ ±
![]() при
при
![]() ,
,
где i − номер влияющей величины.
При этом функция влияния может быть задана аналитически, графически, таблично.
Если функция влияния задана в виде коэффициента влияния, то дополнительная погрешность оценивается по выражению
Δдоп
i ≤ ±
![]() .
.
Например, для одного из вольтметров переменного напряжения влияние температуры на показания вольтметра в НТД задано в следующем виде: «При изменении температуры от нормального значения (20 оС) возникает дополнительная погрешность, равная половине основной погрешности на каждые 10 оС».
Следовательно, если измерения выполняются при температуре окружающей среды, равной 35оС, дополнительная погрешность может составить
Δдоп
i
≤ ±
 =
± 0.75Δосн.
=
± 0.75Δосн.
Погрешность взаимодействия определяется соотношением выходного сопротивления объекта измерений и входного сопротивления измерительного прибора. Например, при измерении переменного электрического напряжения вольтметром с входным сопротивлением Rвх и входной емкостью Свх на выходе объекта с выходным активным сопротивлением Rвых погрешность взаимодействия на основании закона Ома может быть оценена по выражению
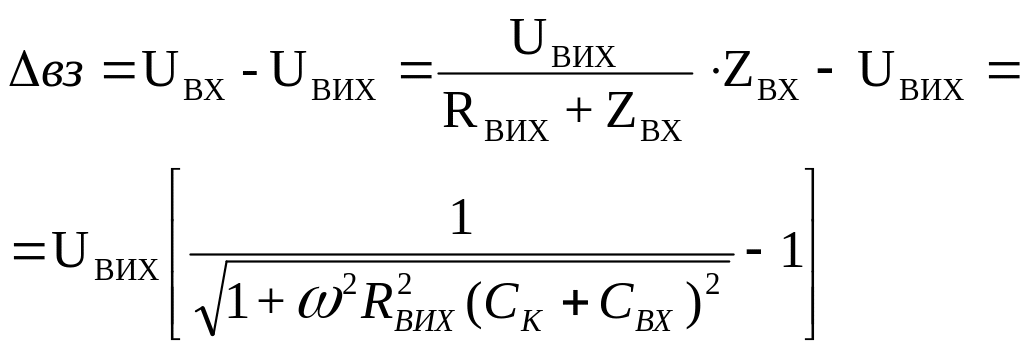 .
.
Из
выражения следует, что при Zвх(jω)
![]()
![]() Δвз
0.
Δвз
0.
Важно иметь ввиду, что при оценке Zвх на частоте необходимо учитывать влияние канала связи (проводного, коаксиального, оптического, теплового и т.п.) между объектом измерений и измерительным прибором.
Динамическую погрешность определить трудно, т.к. чаще всего отсутствует полная информация об инерционных свойствах приборов.
При технических измерениях выбирают такой режим работы прибора, при котором Δдин 0. Это можно сделать, например, если tизм > tуст показаний.
Погрешность от вариации показаний Δвар выписывается из нормативно−технической документации на измерительный прибор.
Суммирование всех составляющих осуществляется по − разному в зависимости от следующих факторов:
−являются составляющие систематическими или случайными;
−случайные погрешности распределяются по нормальному закону или по разным законам;
−являются случайные погрешности независимыми друг от друга или коррелированными.
Таким образом, перед суммированием необходимо провести анализ составляющих. При анализе необходимо учесть одну важную принципиальную особенность метрологических характеристик СИ, нормированных в нормативно−технической документации (НТД) на СИ.
Дело в том, что нормы на метрологические характеристики отражают свойства не отдельно взятого экземпляра СИ, а свойства всей совокупности СИ данного типа. Из этого следует, что метрологические характеристики отдельно взятого экземпляра средства измерения могут быть любыми в пределах области значений, определяемых нормой.
Так, если ≤ 5%, это значит, что погрешность первого экземпляра может быть равна + 1 %, второго − − 3%, третьего − 0%, четвертого − + 4% и т.п. Это значит, что метрологическое характеристики, заданные в виде пределов допускаемых значений (≤а), должны рассматриваться как случайные величины, а поэтому определение общей погрешности должно производиться в виде доверительного интервала.
Систематические погрешности (к таким, чаще всего, относятся погрешность взаимодействия, динамическая погрешность, и некоторые из дополнительных погрешностей) суммируются арифметически с учетом знаков
|
(5.12) |
Остальные составляющие общей погрешности, известные в виде пределов допускаемых значений (в виде интервалов), суммируются статистически в предположении, что они распределены в поле допуска по закону равной вероятности
|
(5.13) |
где k – поправочный коэффициент для принятой доверительной вероятности и числа m составляющих. Для Р = 0,95 коэффициент k = 1,1.
Таким образом, общая погрешность результата измерений составит
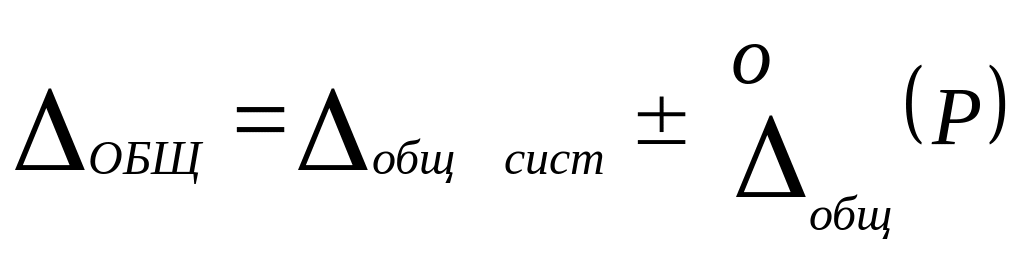 .
.
На систематическую составляющую общей погрешности вводят поправку т.е. к результату измерений алгебраически прибавляют поправку g, которая равна абсолютной систематической погрешности, взятой с обратным знаком.
Пpимеp оценки погрешности при прямых однократных измерениях методом непосредственной оценки.
В соответствии с техническими условиями на узел радиоэлектронного устройства действующее напряжение его выходных сигналов частотой 465 кГц на нагрузке 100 кОм должно быть равно (2,5 0,5) В. Коэффициент гармоник выходных сигналов не превышает 5 %, выходное сопротивление узла составляет 600 Ом 10 %. Hеобходимо оценить возможность применения для допускового контроля напряжения электронного вольтметра типа В3−38. В соответствии с техническим описанием он характеризуется следующими нормируемыми метрологическими характеристиками: пределы основной приведенной погрешности на поддиапазоне измерений 3,0 В и в диапазоне частот 45 Гц...1 МГц − 4%; входное сопротивление − 4 МОм; входная емкость − 15 пФ; емкость придаваемого кабеля − 80 пФ; дополнительная погрешность при изменении температуры относительно нормальной (20 5) °C не превышает основной погрешности на каждые 10 °С. Цена деления шкалы на поддиапазоне 3,0 В равна 0,1 В.
Источники погрешности измерений.
Погрешность измерений напряжения в данном случае складывается из следующих составляющих:
1 − основной погрешности вольтметра;
2 − погрешности от взаимодействия вольтметра с контролируемым узлом, обусловленной соотношением выходного сопротивления узла и входным сопротивлением вольтметра (с учетом кабеля);3 − дополнительной погрешности от влияния неинформативного параметра сигнала − формы кривой измеряемого сигнала;
4 − дополнительной погрешности от влияния внешнего фактора − температуры;
5 − дополнительной погрешности от изменений напряжения сети;
6 − погрешности считывания результата измерений по шкале отсчетного устройства.
Оценка составляющих погрешности.
Поскольку в техническом описании дано значение погрешности, приведенной к конечному значению полдиапазона измерений, т.е.
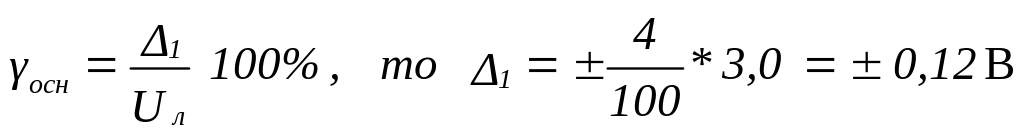
Поскольку эти пределы погрешности даны для всех экземпляров вольтметров данного типа, погрешность конкретного экземпляра будем считать случайной. Полагаем вероятность того, что погрешность примет любое значение в указанных пределах, одинаковой. Среднеквадратичное отклонение погрешности
![]()
Погрешность от шунтирующего действия активного входного сопротивления вольтметра в соответствии с законом Ома
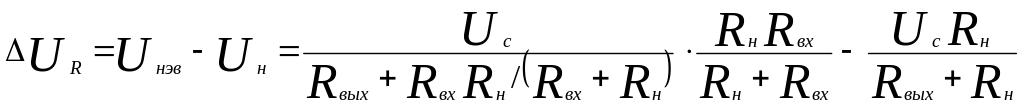 ,
,
где Uн − напряжение на нагрузке узла (100 кОм) до подключения вольтметра; Uнэв − напряжение на нагрузке узла после подключения вольтметра.
Для Uс = 2,5 В; Rвых = 600 Ом; Rн = 100 кОм; Rвх = 4 МОм
![]() ,
,
т.е. шунтирующим действием активного входного сопротивления вольтметра можно пренебречь.
Погрешность от шунтирующего действия емкости кабеля и входной емкости вольтметра (С = Скаб + Свх) определяется аналогично в соответствии с законом Ома:
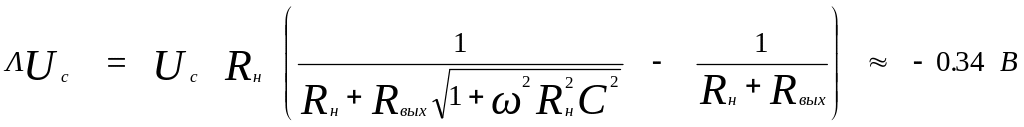
Данная погрешность 2 = Uс является систематической.
Дополнительная
погрешность 3
от формы кривой для вольтметров с
преобразователем средневыпрямленного
напряжения зависит от номера гармоник,
содержащихся в спектре сигнала, и от
фазовых соотношений между ними, однако
в относительных единицах она не превышает
значения
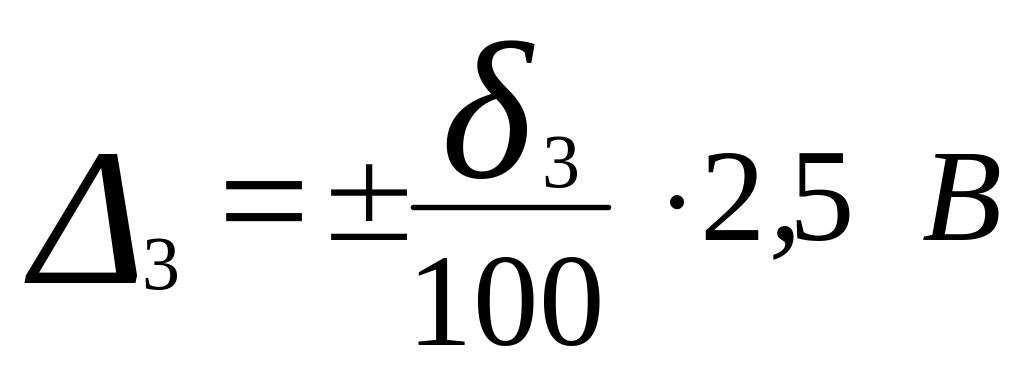 .
.
Здесь
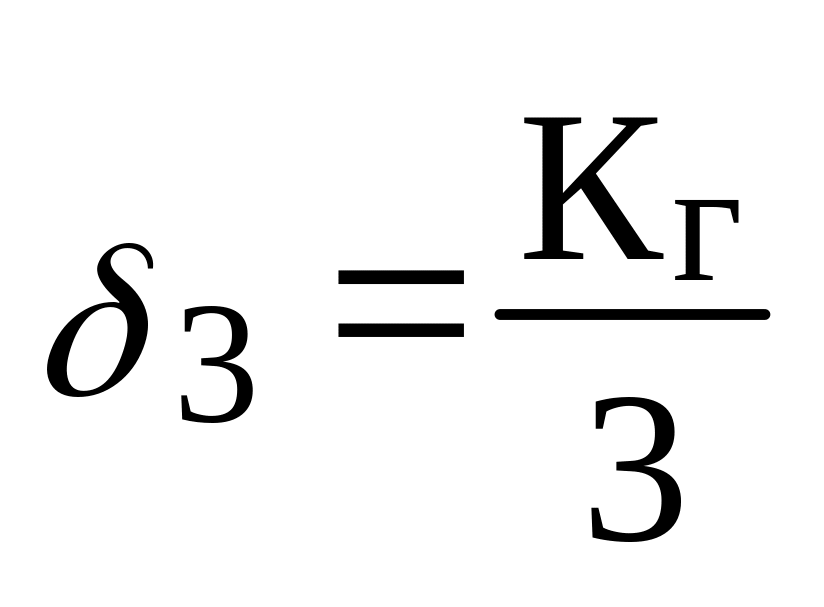 ,
т.е. в данном случае
1,7 %.
,
т.е. в данном случае
1,7 %.
Тогда
![]() .
.
Чаще всего при измерениях номера гармоник и их фазовые соотношения неизвестны, поэтому можно считать данную погрешность случайной и распределенной по закону равной вероятности. СКО данной погрешности
![]() .
.
Дополнительная
погрешность от изменения температуры
4
=
![]() (t − 20), где
(t − 20), где
![]() − коэффициент влияния температуры на
погрешность вольтметра. В соответствии
с техническим описанием
=
0,12 В/10°С. Hаибольшая погрешность будет
при температуре 35°С:
− коэффициент влияния температуры на
погрешность вольтметра. В соответствии
с техническим описанием
=
0,12 В/10°С. Hаибольшая погрешность будет
при температуре 35°С:
![]() .
.
Считая распределение температуры в течение года в пределах от 10 до 35°С равновероятным, получаем СКО данной погрешности
![]() .
.
Погрешность 5 считаем равной нулю, так как в соответствии с техническими данными на вольтметр он сохраняет свои свойства при изменениях напряжения сети в пределах 22 В.
Погрешность считывания 6 не превышает половины цены деления шкалы СЭВ, т.е. 6 = 0,05 В.
СКО данной
погрешности
![]() .
.
Суммиpование погрешностей
Систематическая составляющая общей погрешности
![]() .
.
Случайная составляющая общей погрешности
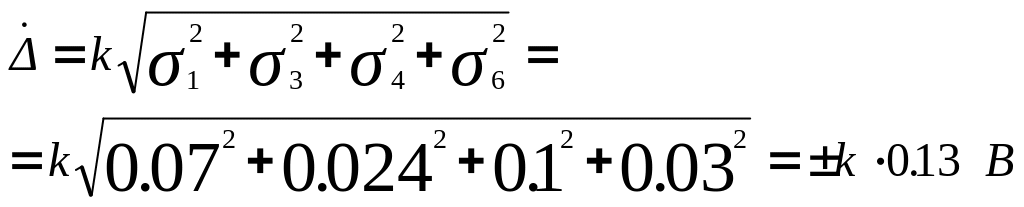 .
.
Коэффициент k
определяется доверительной вероятностью
и законом распределения общей случайной
погрешности. Полагая закон распределения
нормальным (что не совсем справедливо,
так как среди составляющих имеется
доминирующая погрешность 4,
распределенная по закону равной
вероятности) и полагая Р = 0,95, k = 2, получаем
![]() =
0,26 В.
=
0,26 В.
Таким образом,
![]() = (−0,34 ± 0,26) В.
= (−0,34 ± 0,26) В.
Поскольку для допускового контроля погрешность измерений не должна превышать 1/3 допуска (в нашем случае − 0,5 В),
![]() =
1/3 • 0,5
0,17 В,
=
1/3 • 0,5
0,17 В,
данный ЭВ типа В3−38 нельзя применить для контроля напряжения, так как > .
Даже если ввести
поправку на систематическую составляющую
увеличением показаний ЭВ на 0,34 В, т.е.
![]() +
0,34 В, погрешность
+
0,34 В, погрешность
= 0,26 В (Р = 0,95) > 0,17 B.
Доминиpующей погрешностью среди всех составляющих является температурная погрешность 4, поэтому нужно использовать либо ЭВ с меньшим значением коэффициента влияния температуры, либо ужесточить условия выполнения измерений.

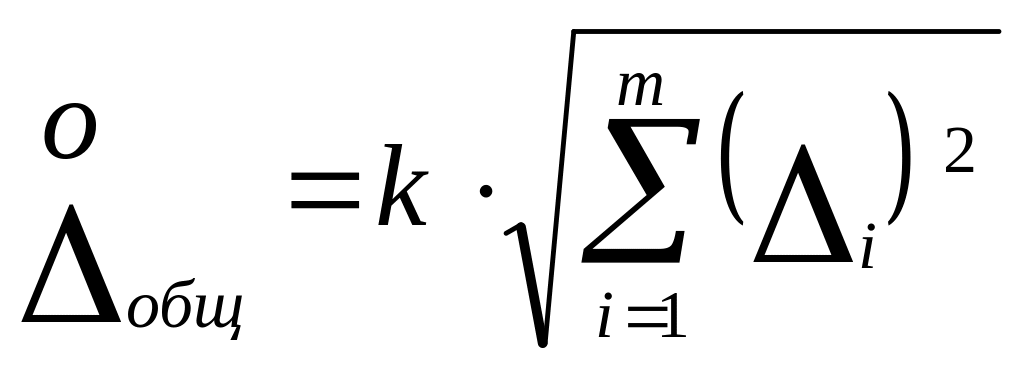 ,
,