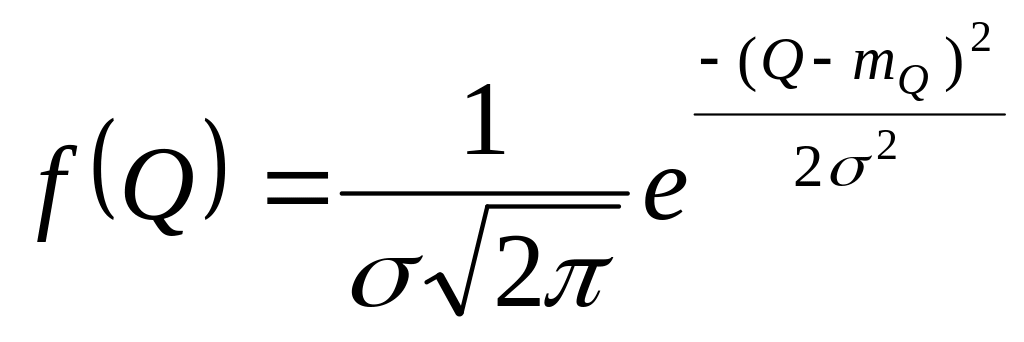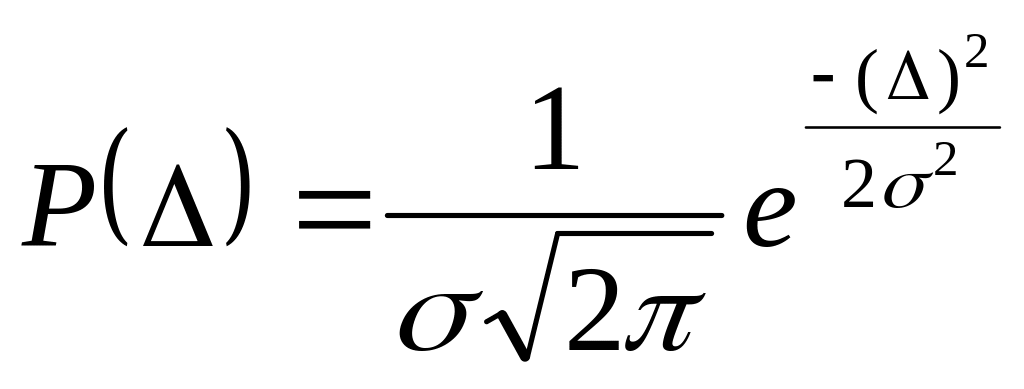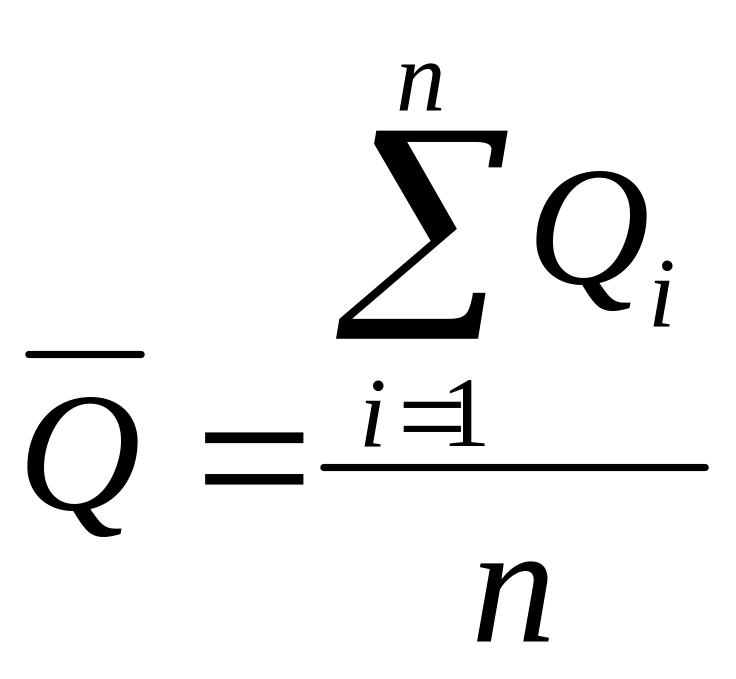Глава 5 похибки вимірювань

5.1 Виды погрешностей и их описание

Целью любого измерения является нахождение истинного значения физической величины в принятых единицах. Вследствие несовершенства средств измерений, воздействия внешних факторов и многих других причин результат каждого измерения неизбежно отягощен погрешностью. Качество измерения тем выше, чем ближе результат измерения оказывается к истинному значению. Количественной характеристикой качества измерений является погрешность результата измерения, − разность между измеренным Q_изм и истинным Q_ист значениями измеряемой величины:

ΔQ = Qизм − Qист,

(5.1)

где ΔQ — погрешность результата измерения (погрешность измерения).

Строго говоря, применение формулы (5.1) для вычисления погрешности измерения невозможно, поскольку истинное значение измеряемой величины неизвестно. Однако, запись погрешности в виде выражения (5.1) несет важную информацию. Так, если погрешность имеет знак +, то это говорит о том, что результат измерений превышает истинное значение величины, если знак минус – то результат измерений меньше истинного значения, а если ±, то он может быть как меньше, так и больше истинного значения и что истинное значение с некоторой оговоренной вероятностью находится в указанных пределах ± ΔQ.

Погрешность, выраженная в единицах измеряемой величины (метрах, вольтах, герцах и т.п.) в соответствии с формулой (5.1), имеет размерность измеряемой величины и называется абсолютной погрешностью измерений. Используется также понятие относительной погрешности — погрешности, выраженной в долях измеряемой величины. Относительные погрешности выражают принятыми в системе СИ относительными величинами: безразмерным числом, в процентах, децибелах (дБ) и др.

Понятие погрешности измерений характеризует как бы несовершенство измерения. Позитивной характеристикой качества измерений является точность измерения. Точность и погрешность связаны обратной зависимостью — измерение тем более точно, чем меньше его погрешность. Количественно точность выражается числом, равным обратному значению относительной погрешности. Так, если погрешность измерения составляет 2*10⁻⁵ ,то точность его 5*10⁴.

Стандартизованной является оценка качества измерения с указанием погрешности. При этом предпочтение отдается выражению погрешности измерения в форме относительной погрешности, как наиболее информативной, дающей возможность объективно сопоставлять результаты и оценивать качество измерений, выполненных в разное время или разными экспериментаторами. В самом деле, измерив длину стержня L = 1000 мм с погрешностью ± 10 мм (т.е. с относительной погрешностью ± 0,01 или ±1 %) и расстояние между двумя объектами L = 1 км с такой же абсолютной погрешностью ± 10 мм (т.е. с относительной погрешностью ±10⁻⁵ или ± 10⁻³ %), мы делаем заключение, что хотя абсолютная погрешность измерения в обоих случаях одинакова, первое измерение является достаточно грубым, а второе выполнено с высокой точностью.

Будучи важнейшей характеристикой результата измерения, определяющей степень доверия к нему, погрешность должна быть обязательно оценена. Для разных видов измерений задача оценивания погрешности может решаться по−разному В соответствии с этим различают измерения с точной апостериорной оценкой, с приближенной апостериорной оценкой и с априорной оценкой погрешности.

При измерениях с точной оценкой погрешности учитываются индивидуальные метрологические свойства и характеристики каждого из примененных средств измерения, анализируется метод измерений, контролируются условия измерений с целью учета их влияния на результат измерения.

При измерениях с приближенной оценкой погрешности учитывают лишь нормативные, типовые метрологические характеристики средств измерения и оценивают влияние на результат измерения лишь отклонений рабочих условий измерения от нормальных условий.

Измерения с априорной (предварительной) оценкой погрешностей выполняются по стандартизированным методикам выполнения измерений, регламентированным нормативно−технической документацией, в которых указываются методы и условия измерений, типы и погрешности используемых средств измерений и, на основе этих данных, заранее оценена и указана в методике возможная погрешность результата.

В инженерной практике обычно имеют дело с измерениями с априорной и приближенной апостериорной оценкой погрешности результата измерения, относящимся к категории технических измерений.

Погрешность результата каждого конкретного измерения складывается из многих составляющих, обязанных своим происхождением различным факторам и источникам. Традиционный аналитический подход к оцениванию погрешностей результата состоит в анализе источников погрешностей, в выделении отдельных составляющих общей погрешности, изучении поведения во времени каждой из них в отдельности и последующем суммировании. Зная свойства и оценив количественные характеристики составляющих погрешностей, можно правильно учесть их при оценивании погрешности результата или, если это возможно, ввести поправки в результат измерения. Выделив и оценив отдельные составляющие погрешности, иногда оказывается возможным так организовать измерение, чтобы эти составляющие не оказали влияния на результат.

Естественно, что классифицировать составляющие погрешности можно по многим признакам. В целях единообразия подхода к анализу и оцениванию погрешностей в метрологии принята следующая классификация.

По характеру проявления во времени выделяют систематические и случайные составляющие погрешности.

Систематической погрешностью измерения называется погрешность, которая при повторных измерениях одной и той же величины в одних и тех же условиях остается постоянной или закономерно изменяется. Источником систематической погрешности может послужить, например, неточное нанесение отметок на шкалу стрелочного прибора, амплитудно−частотная характеристика тракта измерений.

Случайной погрешностью измерения называют погрешность, которая при повторных измерениях одной и той же величины в одних и тех же условиях изменяется случайным образом по знаку и (или) по значению. Случайная составляющая погрешности возможна из−за колебаний напряжения питающей сети, влияния электромагнитных помех и т.п.

При создании средств измерений и организации процесса измерения в целом интенсивность проявления большинства факторов удается свести примерно к одному уровню, так что все они влияют более или менее одинаково на формирование случайной погрешности. Однако некоторые из них, например внезапное падение напряжения в сети электропитания, могут проявиться неожиданно сильно, в результате чего погрешность примет размеры, явно выходящие за границы, обусловленные ходом эксперимента в целом. Такие погрешности в составе случайной погрешности называются грубыми. К ним тесно примыкают промахи − погрешности, зависящие от оператора и связанные с неправильным обращением со средствами измерений, неверным отсчетом показаний или ошибками при записи результатов.

В процессе измерения оба вида погрешностей (систематические и случайные) проявляются одновременно, и погрешность измерения можно представить в виде суммы:

(5.2)

где − случайная, а − систематическая погрешности.

Наиболее наглядным является описание случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей:

(5.3)

Физический смысл f(Δ) состоит в том, что произведение f(Δ)dΔ представляет вероятность попадания случайной величины Δ в интервал от Δ до Δ + dΔ.

Функция распределения является самым универсальным способом описания поведения случайных погрешностей. Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают редко.

Значительно чаще бывает достаточно охарактеризовать случайные погрешности с помощью ограниченного числа параметров, к которым относят:

−математическое ожидание;

−дисперсия результатов наблюдений (или среднее квадратическое отклонение−СКО);

−доверительный интервал.

Дисперсия D[Δ] случайной погрешности является характеристикой рассеивания случайной величины относительно математического ожидания. Дисперсия имеет размерность квадрата измеряемой величины, поэтому она не совсем удобна в качестве характеристики рассеивания. Значительно чаще в качестве последней используется положительное значение корня квадратного из дисперсии, называемое средним квадратическим отклонением результатов наблюдений :

.

(5.4)

Математическое ожидание и дисперсия являются наиболее часто применяемыми параметрами, поскольку они определяют наиболее важные черты распределения случайной величины: положение центра распределения и степень ее разбросанности.

Случайная погрешность измерения образуется под влиянием большого числа факторов, сопутствующих процессу измерения. В каждой конкретной ситуации работает свой механизм образования погрешности. Поэтому естественно предположить, что каждой ситуации может соответствовать свой тип распределения погрешности.

Закон равной вероятности

Значения дифференциальной функции распределения равномерно распределенной случайной погрешности постоянны в интервале [− а; + а], а вне этого интервала равны нулю (рис.5.1).

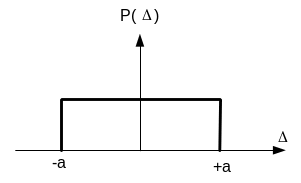
Рисунок 5.1 Закон равной вероятности

Дифференциальная функция равномерного распределения имеет вид:

P(Δ) = с при − a  Δ  +a

P(Δ) = 0 при + a  Δ  − a.

Нормальный закон распределения

(5.6)

где −  − дисперсия результатов наблюдений; − математическое ожидание результатов наблюдений.

Учитывая, что при полном исключении систематических погрешностей для дифференциальной функции распределения случайной погрешности можно записать уравнение

(5.7)

Распределение, описываемое уравнениями (5.6) и (5.7), называется нормальным или распределением Гаусса.

На рис.5.2 изображены кривые нормального распределения случайных погрешностей для различных значений среднеквадратического отклонения .

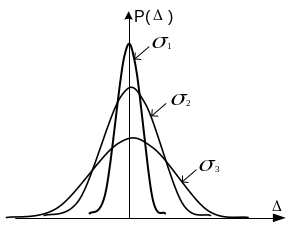
Рисунок 5.2 Нормальный закон распределения вероятностей

Из рисунка видно, что по мере увеличения среднеквадратического отклонения  распределение все более и более расплывается, вероятность появления больших значений погрешностей возрастает, а вероятность меньших погрешностей сокращается, т.е. увеличивается рассеивание результатов наблюдений.

Широкое распространение нормального распределения погрешностей в практике измерений объясняется центральной предельной теоремой теории вероятностей. Центральная предельная теорема утверждает, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдения формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.

Кроме рассмотренных примеров распределений случайных величин существуют и другие важные для практического использования распределения дискретных случайных величин, например, биномиальное распределение и распределение Пуассона. В настоящем пособии они не рассматриваются.

В практике измерений вместо математического ожидания и дисперсии используют их оценки на основании выборки − ряда значений, принимаемых измеряемой величиной в n независимых опытах. Оцениваемыми параметрами являются математическое ожидание и среднеквадратическое отклонение, поскольку только они входят в выражение для дифференциальных функций всех рассмотренных выше распределений.

Оценкой математического ожидания является среднее арифметическое из результатов отдельных наблюдений ,

(5.8)

Оценка дисперсии результатов наблюдений при малом n является немного смещенной, поэтому точечную оценку дисперсии принято определять как

,

(5.9)

а оценку среднеквадратического отклонения результатов наблюдений как

.

(5.10)

Приведенные выше оценки параметров распределения случайных величин в виде среднего арифметического для оценки математического ожидания и СКО для оценки дисперсии называются точечными оценками, так как они выражаются одним числом. Однако в некоторых случаях знание точечной оценки является недостаточным. Наиболее корректной и наглядной оценкой случайной погрешности измерений является оценка с помощью доверительных интервалов.

Симметричный интервал в границами ± ΔQ(Р) называется доверительным интервалом случайной погрешности с доверительной вероятностью Р, если площадь кривой распределения между абсциссами –ΔQ и +ΔQ составляет Р−ю часть всей площади под кривой плотности распределения вероятностей. При нормировке всей площади на единицу Р представляет часть этой площади в долях единицы (или в процентах). Другими словами, в интервале от −Q(Р) до +Q(Р) с заданной вероятностью Р встречаются Р100 % всех возможных значений случайной погрешности.

Доверительный интервал для нормального распределения находится по формуле:

,

где коэффициент t зависит от доверительной вероятности Р.

Для нормального распределения существуют следующие соотношения между доверительными интервалами и доверительной вероятностью: 1 (Р ≈ 0,68), 2 (Р ≈ 0,95), 3 (Р ≈ 0,997).

Доверительные вероятности для выражения результатов измерений и погрешностей в различных областях науки и техники принимаются равными. Так, в технических измерениях принята доверительная вероятность 0,95. Лишь для особо точных и ответственных измерений принимают более высокие доверительные вероятности. В метрологии используют, как правило, доверительные вероятности 0,97, в исключительных случаях 0,99. Необходимо отметить, что точность измерений должна соответствовать поставленной измерительной задаче. Излишняя точность ведет к неоправданному расходу средств. Недостаточная точность измерений может привести к принятию по его результатам ошибочных решений с самыми непредсказуемыми последствиями, вплоть до серьезных материальных потерь или катастроф.

При проведении многократных измерений величины Q, подчиняющейся нормальному распределению, доверительный интервал может быть построен для любой доверительной вероятности по формуле:

,

(5.11)

где t_q – коэффициент Стьюдента, зависящий от числа наблюдений n и выбранной доверительной вероятности Р. Он определяется с помощью таблицы q−процентных точек распределения Стьюдента, которая имеет два параметра: k = n – 1 и q = 1 – P; – оценка среднего квадратического отклонения среднего арифметического.

Доверительный интервал для погрешности Q(Р) позволяет построить доверительный интервал для истинного (действительного) значения измеряемой величины, оценкой которой является среднее арифметическое . Истинное значение измеряемой величины находится с доверительной вероятностью Р внутри интервала: .