9.3 Исследование сигналов в частотной области

9.3.1 Общие сведения о спектре сигналов

Осциллографические средства измерений позволяют отобразить на экране электрические процессы в цепях в виде зависимости напряжения от времени.

Однако, такой способ анализа сигналов во временной области имеет тот недостаток, что он не обладает достаточно высокой чувствительностью к изменениям (искажениям, деформациям) сигнала при распространении его по цепям. То есть на экране осциллографа изменений сигнала, если они невелики (например, Кг ≤ 3 %), не видно.

Эти изменения можно обнаружить, если сигнал наблюдать не во временной области, а в частотной, то есть, если рассматривать сигнал как сумму гармонических составляющих (синусоид) с различными и неизменными во времени частотами, различными амплитудами и различными начальными фазами (9.16):

,

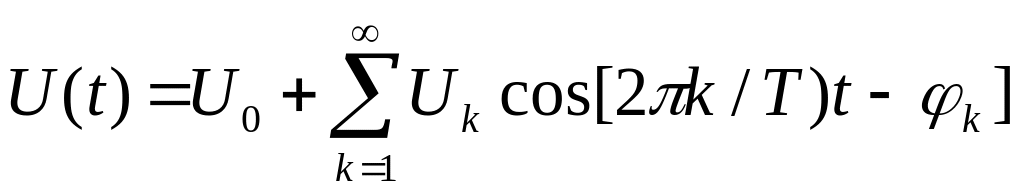(9.16)

Здесь − постійна складова сигналу, Т – період, k − номер гармоніки, U_k− амплітуда k−ї гармоніки, f_k= k/T i _k − її частота і фаза.

Сукупність величин називають спектром амплітуд, сукупність величин − спектром фаз,  = 2f − кутова частота.

При измерениях цікавляться, як правило, тільки амплітудним спектром.

Теоретичні спектри періодичного сигналу мають лінійчасту структуру, яка графічно виглядає як вертикальні лінії вздовж вісі частот у точках f₁, 2f₁, 3f₁, ..., кf₁ і далі до нескінченності з кроком f₁. Висота кожної з спектральних ліній пропорційна амплітуді U_k (рис. 9.9,а) чи фазі _k к−ї спектральної складової (рис. 9.9,б).

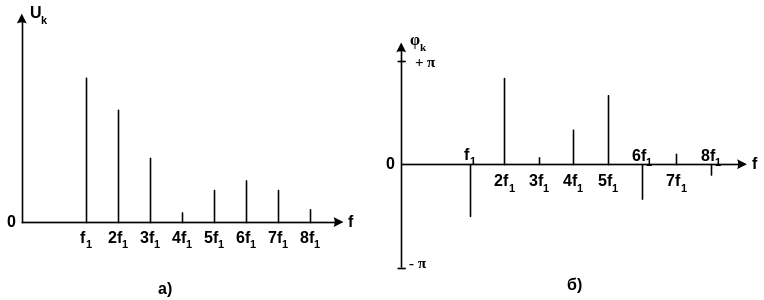
Рисунок 9.9 — К понятию амплитудного (а) и фазового (б) спектра сигнала

Вид огибающей спектра определяется формой сигнала.

Для количественной оценки амплитудного спектра пользуются следующими параметрами:

− значения частот гармонических составляющих;

− значения амплитуд гармонических составляющих (или отношения амплитуд отдельных составляющих);

− вид огибающей амплитуд спектра и наиболее характерные точки огибающей;

− ширина спектра, под которой понимают интервал частот, где сосредоточена основная часть энергии сигнала (обычно это главный и два боковых лепестка огибающей).

Приборы, предназначенные для визуального исследования амплитудно−частотного спектра колебаний, и значения отношений амплитуд отдельных гармоник и их частот, называют анализаторами спектра.

Параметры аппаратуры, измеряемые при помощи АС:

− уровень амплитудных, частотных и фазовых шумов в компонентах электронной аппаратуры, их линейность;

− ширина спектра, стабильность частоты источников сигнала; их устойчивость к изменениям напряжения питания, нагрузки, прогреву;

− АЧХ различных узлов;

− степень экранирования, развязка между входами;

− измерение параметров модулированных колебаний.

Функціональне перетворення аналогового детермінованого сигналу неперіодичної форми з часової площини в частотну здійснюється перетворенням Фур’є U(t)U() за формулої (9.17).

.

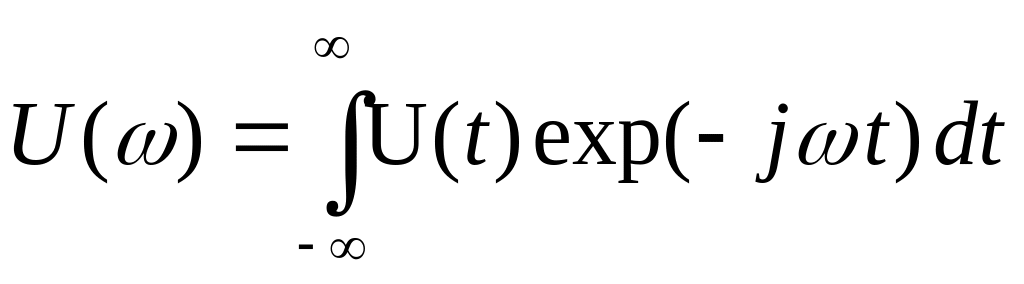(9.17)

9.3.2 Виды анализаторов спектра

Поширеним способом апаратурного аналізу спектру є перетворення Фур’є як результату впливу досліджуваного сигналу на вузькосмугові фільтри. Такі способи спектрального аналізу дістали назву фільтрових.

Перевагу надають панорамному аналізаторові спектру послідовного типу з гетеродинним перетворенням. Такий спосіб аналізу спектру − послідовний, требует одного перестраиваемого резонатора, просматривающего весь диапазон анализируемых частот.

АС последовательного типа представляют собой объединение супергетеродинного приемника, выполняющего роль узкополосного перестраиваемого фильтра, и осциллографа (рис.9.10).

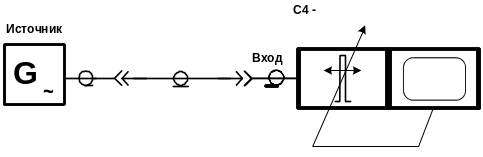
Рисунок 9.10 — Схема анализа амплитудного спектра сигнала

Существенно, что этот перестраиваемый фильтр в пределах анализируемого диапазона частот перестраивается автоматически благодаря модуляции гетеродина приемника по частоте с помощью пилообразного напряжения, которое одновременно используется для горизонтальной развертки луча ЭЛТ.

Каждому положению луча ЭЛТ соответствуют строго определенная частота гетеродина и частота анализируемого сигнала, что позволяет проградуировать ось X осциллографа в значениях частоты (а не времени, как в осциллографе).

При перестройке гетеродина все составляющие гетеродина последовательно будут попадать в полосу пропускания усилителя промежуточной частоты (УПЧ). Таким образом, с выхода УПЧ будут сниматься радиоимпульсы с частотой заполнения, равной ПЧ и амплитудой, пропорциональной спектральной составляющей сигнала. На экране ЭЛТ составляющие спектра будут представляться как выбросы, ширина которых определяется формой АЧХ УПЧ.

Спектрограма на дисплеї АС матиме лінійчасту структуру, в якій кожна з спектральних ліній відображатиме форму динамічної АЧХ аналізуючого фільтра. На рис. 9.11,а наведено апаратурний спектр сигналу, який відповідає теоретичному амплітудному спектру на рис. 9.9 а. Відмінності у формі спектральних ліній викликані явищем, яке має назву динамічна АЧХ вузькосмугового фільтра.

Воно виникає, коли АЧХ такого фільтра спостерігають не в спосіб точка за точкою (статична характеристика 1 на рис. 9.11,б), а при неперервному зміненні частоти синусоїдного сигналу на вході (чи перестроюванні центральної частоти фільтра). При цьому внаслідок інерційності фільтра з підвищенням швидкості змінення частоти (АЧХ 2 і 3 на рис. 9.11,б) спотворення статичної характеристики 1 збільшуються: − зсуваються екстремуми, розширюється смуга частот f (тобто погіршується роздільна здатність аналізатора), характеристика стає асиметричною.

Время анализа зависит от ширины исследуемой области частот f_c= f_max − f_min и избирательности анализируемого фильтра. Если анализ в полосе частот фильтра Δf_пч происходит за время t= 1/Δf_пч, то полное время анализа Т_а = f_c/(f_пч)². Как видно, с уменьшением полосы Δf_пч время анализа резко увеличивается. Поэтому при разрешающей способности по частоте в единицы Гц последовательный анализ не применяется.

Апаратурний спектр сигнала (а) та динамічна АЧХ вузькосмугового фільтра (б) Рисунок 9.11 – К искажениям спектра сигнала

Частотный диапазон АС снизу ограничен минимальным значением 10 Гц. На более низких частотах применяют цифровой анализ спектра.

Паралельний фільтровий аналізатор

Аби максимально зменшити допустимий термін фільтрового аналізу, застосовують паралельний (багатоканальний) спосіб фільтрового аналізу. На виході кожного з m вузькосмугових фільтрів одержують напругу, пропорційну значенню амплітудного спектру на центральній частоті цього фільтра f_m. Числове значення цієї напруги зберігається в аналоговому запам’ятовуючому пристрої. Комутатор за один цикл роботи послідовно зчитує вміст кожного запам’ятовуючого пристрою. За один цикл обертання комутатора всі канали обробки будуть по черзі підключені до вертикального входу дисплея. Розгортання зображення на дисплеї здійснюється тим самим сигналом Х, який обертає комутатор за один цикл. З принципу роботи паралельного аналізатора видно, що він здатний аналізувати сигнали лише з суцільним спектром, чого не може робити послідовний аналізатор. Роздільна здатність паралельного аналізатора визначається смугою частот аналізуючого фільтра f. Достоинства: малое время анализа, можно анализировать спектры редкоповторяющихся и одиночных импульсов. Недостатки: сложность системы фильтров.

Цифровий аналіз спектру

Цифровий аналіз спектру спирається на відповідне дискретне перетворення Фур’є (9.18):

.

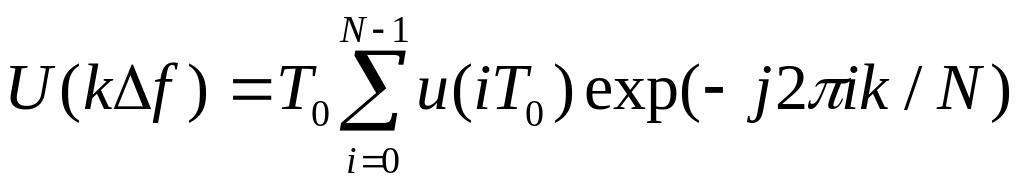(9.18)

При апаратурному одержанні послідовності відліків u(іТ_о) неперервний сигнал u(t) регулярно дискретизують з інтервалом Т_о (і = 0, 1, 2, ..., N−1) на загальному інтервалі спостереження Т = Nт_о. Тепер послідовність u(іТ_о) сприймають як періодичну функцію в часовій площині з періодом Т. Відповідну їй функцію частоти U(kf) в частотній площині розглядають у дискретних значеннях k частоти з інтервалами f = 1/Nт_о (k = 0, 1, 2, ..., N−1). Отже, формула (9.18) являєть собою перетворення Фур’є U(kf)U(іТ_о).

Обробка даних при безпосередньому виконанні дискретного перетворення Фур’є (ДПФ) за формулої (9.18) потребує приблизно N ² арифметичних операцій. З формули (9.18), наприклад, видно, що кожне U(kf) є сумою (N−1) комплексних добутків u(іТ_о)exp(−j2ik/N), кожен з яких, в свою чергу, визначають за результатами чотирьох перемножень і двох складань дійсних чисел. Для прискорення процедур перетворення існують спеціальні стандартні алгоритми, які скорочують тривалість дискретного перетворення Фур’є. Такі, оптимальні за обсягом обчислювальних операцій алгоритми, дістали назву алгоритмів швидкого перетворення Фур’є (FFT − Fast Fourier Transform).

В порівнянні з фільтровими аналоговими аналізаторами цифрові спектроаналізатори мають більше сервісних можливостей при значному розширенні функціональних можливостей і зниженні похибки аналізу. До недоліків варто віднести обмеженість частотного діапазону внаслідок відносно невисокої швидкодії і малого динамічного діапазону АЦП.