5.5.2 Уменьшение случайной погрешности

Многократные наблюдения выполняют в том случае, если систематические погрешности уменьшены, а случайные погрешности превышают систематические. В этом случае многократные наблюдения позволяют уменьшить случайную погрешность результата путем статистической обработки результатов наблюдений.

Порядок обработки результатов многократных наблюдений регламентирован ГОСТ 8.207−76.

При статистической обработке результатов многократных наблюдений (предполагается, что n ≥ 4)следует выполнять следующие операции:

1 Исключить из каждого наблюдения Q_i известную систематическую погрешность и получить исправленный результат отдельного наблюдения Q_i.

2 Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения:

3 Вычислить оценку среднего квадратического отклонения отдельных наблюдений относительно среднего арифметического:

.

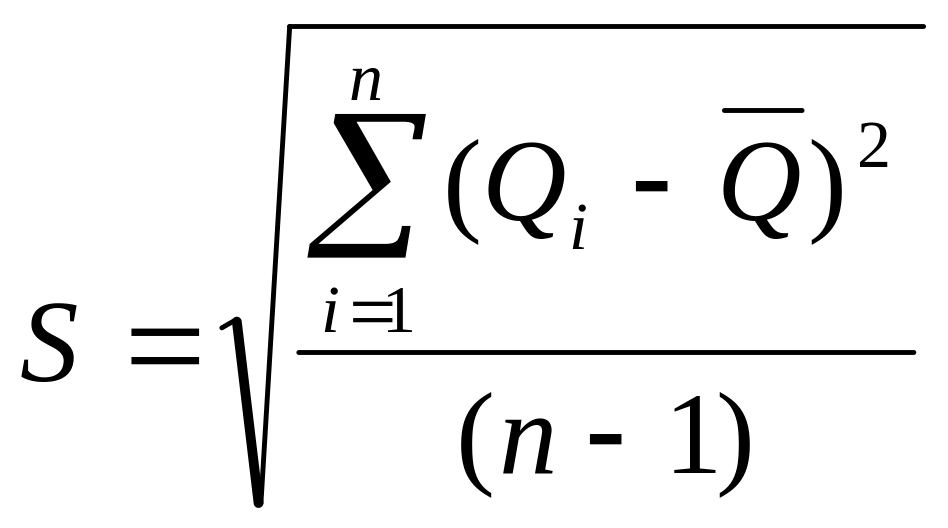4 Проверить наличие грубых погрешностей – нет ли значений , которые выходят за пределы 3S. При нормальном законе распределений с вероятностью, практически равной 1 (0,997), ни одно из значений этой разности не должно выйти за указанные пределы. Если они имеются, то следует исключить из рассмотрения соответствующие значения и заново повторить вычисления и оценку S.

5 Вычислить оценку СКО результата измерения (среднего арифметического) относительно математического ожидания:

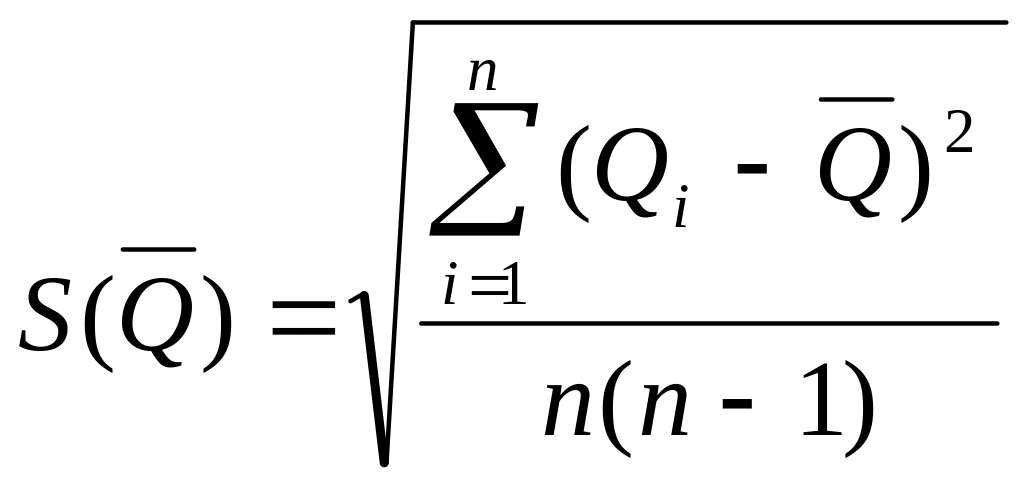
6 Проверить гипотезу о нормальности распределения результатов наблюдений.

Существуют различные приближенные методы проверки нормальности распределения результатов наблюдений. Некоторые из них приведены в ГОСТ 8.207−76. При числе наблюдений меньше 15 в соответствии с этим ГОСТ принадлежность их к нормальному распределению не проверяют. Доверительные границы случайной погрешности определяют лишь в том случае, если заранее известно, что результаты наблюдений принадлежат этому распределению. Приближенно о характере распределения можно судить, построив гистограмму результатов наблюдений. Математические методы проверки нормальности распределения рассматриваются в специальной литературе. На практике нередко бывает, что выбрать тип распределения погрешности нелегко, а проверка гипотез сигналов с одним из стандартных распределений либо не может быть выполнена, либо дает отрицательные результаты.

В этом случае результат измерения в доверительный интервал оценивают так, как будто погрешность распределена нормально, имея при этом в виду, что при разных законах распределения, но одинаковых S (СКО) доверительный интервал будет оценен с завышением (примерно на 20 %).

7 Вычислить доверительные границы  случайной погрешности (случайной составляющей погрешности) результата измерения

где t_q − коэффициент Стьюдента, зависящий от числа наблюдений и доверительной вероятности. Например, при n = 14, P = 0,95 t_q = 2,16. Значения этого коэффициента приведены в приложении к указанному стандарту.

8 Вычислить границы суммарной неисключенной систематической погрешности (НСП) результата измерений  .

Границы неисключенной систематической погрешности  при числе слагаемых большим или равным 4 вычисляются по формуле:

где − граница i−ой составляющей погрешности; k − коэффициент, определяемый доверительной вероятностью. При Р = 0,95 k = 1.1, при Р = 0,99 k = 1,4.

При числе слагаемых меньших или равных 3 значения суммируются арифметически по модулю. Если же суммировать НСП арифметически при любом числе слагаемых, то полученная оценка будет хотя и надежной, но завышенной.

Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что при вычислении доверительных границ случайной погрешности.

9 Проанализировать соотношение  и :

Если , то НСП по сравнению со случайными погрешностями пренебрегают, и граница погрешности результата  =± . Если  8, то случайной погрешностью можно пренебречь и граница погрешности результата  = Θ. Если оба неравенства не выполняются, то границу погрешности результата находят путем построения композиции распределений случайных погрешностей и НСП по формуле: , где К – коэффициент, зависящий от соотношения случайной погрешности и НСП; S_ − оценка суммарного СКО результата измерения. Оценку суммарного СКО вычисляют по формуле:

.

Коэффициент К вычисляют по эмпирической формуле:

.

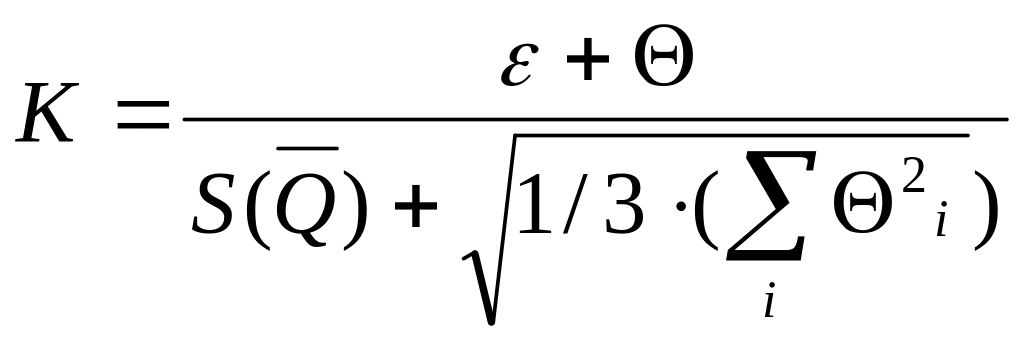Доверительная вероятность для вычисления и должна быть одной и той же.

Увеличивать число наблюдений при многократных измерениях целесообразно до тех пор, пока доверительная погрешность измерения не будет определяться только ситематической погрешностью.

Из соотношений 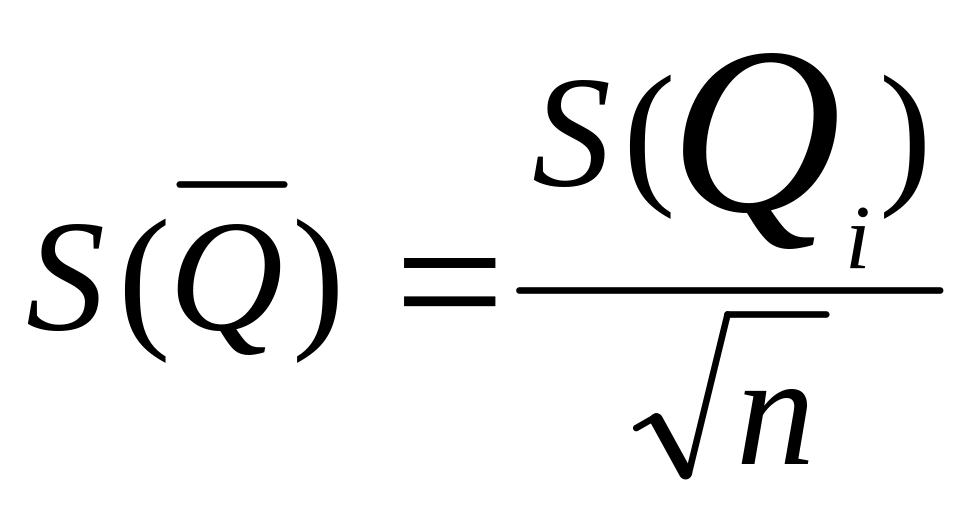и  8 следует, что максимальное число наблюдений

(5.20)

10 Записать результат измерений. Написание результата измерений предусмотрено в двух вариантах, так как следует различать измерения, когда получение значения измеряемой величины является конечной целью, и измерения, результаты которых будут использоваться для дальнейших вычислений или анализа.

В первом случае достаточно знать общую погрешность результата измерения и при симметричной доверительной погрешности результаты измерений представляют в форме: .

Во втором случае должны быть известны характеристики составляющих погрешности измерения – оценка среднего квадратического отклонения результата измерения , границы НСП , число выполненных наблюдений . При отсутствии данных о виде функций распределения составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей, результаты измерений представляют в форме: .

Оценки , и производные от их величины могут быть выражены как в абсолютной форме, то есть в единицах измеряемой величины, так и в относительной форме, то есть как отношение абсолютного значения данной величины к результату измерения.