5.5 Способы достижения требуемой точности

Задача достижения требуемой точности является одной из главных задач метрологии.

Поскольку общая погрешность результата измерений, как правило, складывается из систематической и случайной составляющих, а систематические погрешности бывают постоянные и изменяющиеся, данная задача распадается на три различных ситуации:

1 как обнаружить и уменьшить постоянную систематическую погрешность;

2 как обнаружить и уменьшить изменяющуюся систематическую погрешность;

3 как обнаружить и уменьшить случайную погрешность.

Способы обнаружения и уменьшения погрешности различны в зависимости от стадии измерительного эксперимента: при подготовки к измерениям; при выполнении измерения и при обработке результатов измерений.

5.5.1 Способы уменьшения постоянной систематической погрешности

Обнаружение и исключение систематических погрешностей представляет собой сложную задачу, требующую глубокого анализа всей совокупности результатов наблюдений, используемых средств, методов и условий измерений. При этом необходимо отметить, что устранение систематических погрешностей осуществляется не путем математической обработки результатов наблюдений, а применением специальных приемы проведения измерений, которые позволяют исключить часть систематических погрешностей.

На этапе подготовки к измерениям могут быть использованы следующие способы.

1 Изучение и выполнение требований инструкции по эксплуатации средства измерений: прогрев в течение заданного интервала времени; предварительная калибровка встроенным калибратором; установка «нуля» и т.п.

2 Создание (по возможности) рабочих условий выполнения измерения близких к нормальным, при которых проводилась градуировка средства измерений, что позволяет исключить дополнительные погрешности (стабилизация напряжения сети, кондиционирование помещения, экранирование рабочего места и т.п.).

3 Метрологическая аттестация средства измерений на некоторых поддиапазонах измерений с целью точного определения систематической погрешности с дальнейшим введением на нее поправки в результат измерений. Данная процедура выполняется метрологической службой предприятия или территориальным органом Госстандарта, которые располагают образцовыми средствами измерений (рабочими эталонами).

4 Анализ схемы измерений с целью получения аналитического выражения для искомой погрешности, с дальнейшей ее оценкой и введением поправки в результат измерений. Используя модели ОИ и СИ, выявляют погрешности, которые могут быть оценены (описаны) аналитически. Это позволяет рассчитывать погрешности и устранять их путем введения поправок. Согласно этому способу к результату измерений алгебраически прибавляют поправку g, которая равна абсолютной систематической погрешности, взятой с обратным знаком.

Пример: абсолютная погрешность взаимодействия вольтметра В3−38, обусловленная его входным сопротивлением и входной емкостью при измерении переменного напряжения с частотой F (МГц) и выходным сопротивлением обьекта Z_вых(j) (см. пример в подразделе 3.2) составила − 0,34 В, а результат измерений U~ составил 3,0 В. Поправка g = − (− 0,34 В) = + 0,34 В, а U_ист = U_изм + g = 3,0 В + 0,34 В = 3,34 В.

Таким же образом необходимо поступать со всеми известными систематическими погрешностями.

На этапе выполнения измерений используют следующие способы.

Реализовать метод замещения.

Рисунок 5.7 – К методу замещения

На первом этапе считывают показание прибора

,

а на втором этапе, после подключения вместо объекта измерений регулируемой меры, добиваются показания прибора

.

Из данных соотношений следует, что систематическая погрешность входит с одинаковым знаком в обе части уравнения и потому исключается:

.

Необходимо отметить, что при реализации данного способа необходимо, чтобы неинформативные параметры объекта измерений и меры были идентичны, в противном случае могут появиться дополнительные погрешности.

Рандомизация систематической погрешности :

Идея этого способа заключается в том, что систематическая погрешность при других опытах должна повторяться (проявляться) по − разному. Тогда, измерив параметр несколько раз, и усреднив результаты отдельных измерений по соотношению

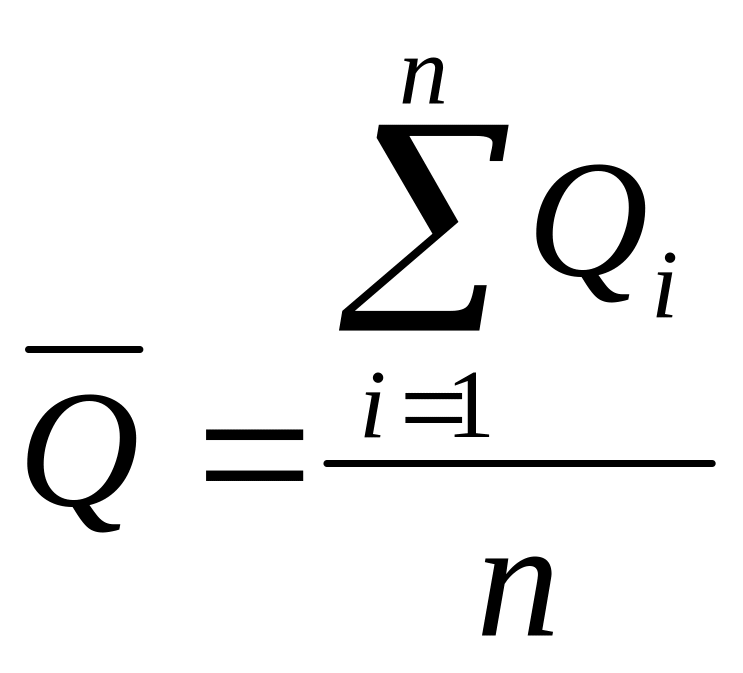
получим среднее арифметическое, более близкое к истинному значению Q_ист., чем любой из отдельных результатов Q_i .

Пример: измерение интервала времени при помощи осциллографа через сравнение этого интервала с метками частоты, подаваемых от генератора точной частоты на вход Z осциллографа. Выполняя несколько измерений этого интервала при разных, но близких значениях частоты меток, заставляем систематическую погрешность изменять как значение, так и знак, т.е. переводим систематическую погрешность в разряд случайных для результата измерений.

Способ инвертирования (способ двойных измерений) заключается в том, что измерения проводят дважды, причем таким образом, чтобы причина, вызывающая погрешность при первом измерении, оказывала противоположное действие на результат второго измерения.

Если Q₁ = Q_ист + ; а Q₂ = Q_ист −  , то результат измерений Q_ист = (Q₁ + Q₂)/2 не содержит систематической погрешности.

Например, это относится к вариации показаний СИ от направления подхода к результату измерений (от нижних значений и от верхних значений).

Все рассмотренные способы рассмотренные способы распространяются на постоянные систематические погрешности.

На этапе обработки результатов измерений можно обнаружить только изменяющуюся систематическую (а также уменьшить случайную) погрешность, а обнаружить и исключить постоянную систематическую погрешность нельзя.

Наиболее простой способ обнаружения изменяющейся систематической погрешности – графический. Для этого, после вычисления среднего арифметического значения , вычисляют отклонения dQ_i каждого из результатов Q_i от среднего арифметического: dQ_i = Q_i − .

Затем строят график зависимости этих отклонений от номера наблюдения: dQ_i = f(n).

Пример построения такой зависимости dQ_i = Q_i − = f(n) показан на рис.5.8.

Из рис.5.8. видно, что, несмотря на случайные изменения, последовательность отклонений результатов наблюдений от среднего значения dQ_i = Q_i − обнаруживает тенденцию к убыванию (или к возрастанию в иных случаях ).

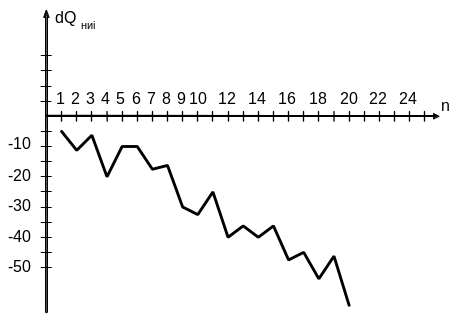
Рисунок 5.8 – График зависимости dQ = f(n)

Для того, чтобы исправить результаты наблюдений введением в них поправки на изменяющуюся систематическую погрешность, необходимо выяснить характер зависимости погрешности.

Чаще всего эту зависимость удается аппроксимировать линейной зависимостью вида

Q(t) =  +  t,

(5.18)

где  и  − параметры прямой; t − время наблюдения (или иной неслучайный параметр, характеризующий условия проведения измерений ).

Значения  и  определяются методом наименьших квадратов из выражений

, ; где ,

(5.19)

После чего в массив исходных результатов многократных измерений вносят поправки на изменяющуюся систематическую погрешность

Q_{испр i} = Q_i −  t_i.

Изменяющую систематическую погрешность можно также обнаружить статистическим способом, который выполняется следующим образом:

− разбивают все наблюдения Q_i на группы по 4−5 наблюдений в группе: (Q₁−Q₄)(Q₅−Q₈)(Q₉−Q₁₂)..и т.д..;

− вычисляют групповые средние , , и т.д.

− по критериям Аббе и Бартлетта проверяют, допустимы ли расхождения между групповыми средними, если эти расхождения считать случайными. Если расхождения между нельзя считать случайными, то уравнение для изменяющейся систематической погрешности Q_{испр i} = f(t_i) определяют регрессионным анализом с последующим введением поправок в результаты наблюдений.

Еще один способ уменьшения изменяющейся систематической погрешности − выполнение симметричных наблюдений. Способ симметричных наблюдений заключается в проведении многократных наблюдений через равные промежутки времени и в усреднении результатов наблюдений, расположенных относительно среднего наблюдения симметрично. Способ эффективен только для систематической погрешности, изменяющейся по линейному закону.

Как отмечалось ранее, известные систематические погрешности устраняются путем введения поправок, которые находятся разными путями и представляют собой значения абсолютных погрешностей, которые вычитаются из результата измерений. Но введение поправок не исключает полностью систематические погрешности, так как остаются, например, погрешности определения поправок. Эти неисключенные части представляют собой неисключенные остатки систематических погрешностей (НСП).

Неисключенная систематическая погрешность характеризуется границей каждой ее составляющей.

В связи с этим возникает задача суммирования НСП. При этом НСП должны рассматриваться как случайные величины и суммироваться методами теории вероятностей, что предполагает знание функции распределения этих составляющих. Однако, закон распределения элементарных составляющих погрешности, как правило, неизвестен. Поэтому при суммировании руководствуются следующим практическим правилом, основанном на опыте и интуиции: при отсутствии дополнительной информации о законах распределения неисключенные остатки систематической погрешности рассматриваются как случайные величины, имеющие равномерное распределение.

В соответствии с этим правилом границы неисключенной систематической погрешности  при числе слагаемых большим или равным 4 вычисляются по формуле:

где − граница i−ой составляющей погрешности; k − коэффициент, определяемый доверительной вероятностью. При Р = 0,95 k = 1.1, при Р = 0,99 k = 1,4.

При числе слагаемых меньших или равных 3 значения суммируются арифметически по модулю. Если же суммировать НСП арифметически при любом числе слагаемых, то полученная оценка будет хотя и надежной, но завышенной.
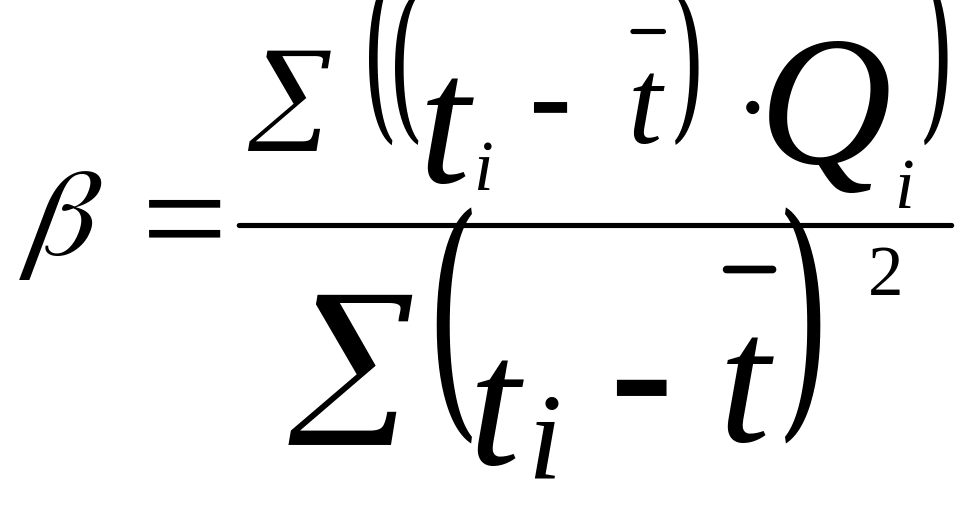