Завдання для розрахунково – графічних та контрольних робіт

Розрахунково - графічні або контрольні роботи з теоретичної механіки виконуються в зошиті шкільного зразку, на обкладинці якого вказуються назва роботи, курс, група, прізвище та ініціали студента, варіант роботи. Виконання кожного завдання починається з його назви на новій сторінці. Номер варіанту завдань дає викладач.

Перед тим як проводити розрахунки , треба добре розібратися в умовах задачі і схеми до неї. При цьому треба головну увагу звертати на механічний загальний зміст завдання ( рівновагу тіла, дію механізму, рух системи, тощо).

Рисунки схем мають бути виконані з допомогою креслярського приладдя, чітко і акуратно. На них мають бути показані всі атрибути, необхідні для виконання завдання (вектори, розміри, осі координат і все інше). Розрахунки слід супроводжувати короткими поясненнями, як це зроблено у відповідних прикладах.

При виконанні завдань треба звернути увагу на слідуюче. Механіка є наука природознавча , про взаємодію і рух реальних макротіл у просторі та часі. Тому головним при практичному використанні теоретичної механіки є математичне описання (формулювання) механічних умов задачі (її постановка). Якщо це зроблено у відповідності з законами механіки і за її правилами, тоді така задача завжди має розв’язок просто тому, що стан тіла, або тіл, який математично описується в задачі, відбувається насправді у природі. Це дає можливість контролювати за тим, чи правильно розв’язується задача ще в процесі цього розв’язання. В першу чергу це робиться за розмірністю. Якщо в задачі виникла необхідність складати (віднімати) величини різних розмірностей (кілограми з метрами , ньютони з секундами і таке інше) це означає, що десь зроблена помилка і задача розв’язується неправильно. З другого боку, якщо при розв’язанні задачі одержано від’ємний час, додатна робота сили опору, від”ємна кінетична енергія або ще якась фізична величина, яка не існує в природі макросвіту, це означає, що десь зроблено помилку і задача розв”язується неправильно. Наведені правила дають можливість контролювати хід розв”язання задач механіки на всіх етапах.

При виконанні завдань треба керуватися вказаною для кожної задачі теорією і прикладами розв”язання аналогічних задач, приведених в посібнику “Основи теоретичної механіки” та в інших підручниках і розробках з теоретичної механіки.

Завдання к. Кінематіка

Задача К1. КІНЕМАТІКА ТОЧКИ. Визначення кінематичних характеристик руху точки.

За даними рівняннями руху точки М визначити:

а) рівняння траєкторії точки і зобразити траєкторію на рисунку;

б) швидкість й прискорення точки для моменту часу t₁ ;

в) для моменту часу t₁ знайти положення точки М на траєкторії і показати вектори швидкості, дотичного, нормального та повного прискорень;

г) радіус кривізни траєкторії в момент часу t₁ .

Дані задачі наведені в таблиці 1 завдань: теорія в параграфах 1-5, а приклад в параграфі 7 глави 1, розділу 1 посібника «Основи теоретичної механіки».

Необхідно знати:

1. Способи завдання руху точки.

2. Формули, за якими визначаються проекції на декартові осі координат вектора швидкості та вектора прискорення точки.

3. Величини нормального та дотичного прискорень точки.

4. Формули, за якими визначається аналітично будь-який вектор, якщо відомі його проекції на осі координат.

Необхідно вміти:

1. Діставати похідні від різних функцій.

2. Використовувати різні тригонометричні тотожності.

Задача К2. ПРОСТІ ВИДИ РУХІВ ТВЕРДОГО ТІЛА ТА ЇХ ПЕРЕТВОРЕННЯ.

Визначення швидкостей і прискорень точок твердого тіла при поступальному і обертальному рухах.

За даними рівняннями прямолінійного поступального руху тягара 1 визначити і показати на малюнку швидкість, дотичне, нормальне та повне прискорення точки М механізма, якщо тягар пройшов шлях S.

Схеми механізмів показані на рис. 1, а необхідні дані наведені в таблиці 2 завдань: теорія в параграфах 1-4, а приклад з задачею в параграфі 5 глави 3 розділу 1 посібника.

Необхідно знати:

1.Основну теорему поступального руху тіла.

2. Формули, що за заданим законом S=S(t) поступального прямолінійного руху тіла визначають його швидкість і прискорення.

3. Формули, що за заданим законом обертального руху твердого тіла навколо нерухомої осі j=j(t) визначають його кутову швидкість і кутове прискорення.

4. Формули, за якими визначається швидкість і прискорення будь-якої точки тіла, що обертається навколо нерухомої осі.

5. Якщо обертання від одного тіла до другого передасться безпосереднім дотиком або за допомогою ременя, тоді кути обертання цих тіл (коліс), їх кутові швидкості і кутові прискорення обернено пропорційні їх радіусам (числам зубців Z):

.

Необхідно вміти:

1. Класифікувати прості рухи твердого тіла.

2. Диференціювати різні функції.

3. Геометрично складати два вектори.

Задача К3. КІНЕМАТИЧНИЙ АНАЛІЗ ПЛОСКОГО МЕХАНІЗМУ.

Для заданного положення механізму знайти швидкість і прискорення точки В, а також кутову швидкість і кутове прискорення ланки, яка робить плоский рух. Схеми механізмів показані на рис. 2, необхідні дані наведені в таблиці 3 завдань: теорія в параграфах 1-4, а приклад - в параграфі 5 глави 4 розділу 1 посібника.

Необхідно знати:

1. Формулу, що визначає швидкість точки М твердого тіла, яка робить плоский рух.

2. Поняття миттьового центру швидкостей (м.ц.ш.).

3. Теорему про проекції швидкостей двох точок плоскої фігури.

4. Теорему про прискорення точок плоскої фігури.

Необхідно вміти:

1. Класифікувати рухи ланок плоского механізму.

2. Визначати положення миттьового центру швидкостей ланки, що робить плоский рух, як м.ц.ш. плоскої фігури.

3. Використовувати поняття м.ц.ш. для визначення швидкостей точок плоскої фігури.

4. Аналітичне додавати вектори і визначати їх суму.

Задача К4. СКЛАДНИЙ РУХ ТОЧКИ. Визначення абсолютної швидкості і абсолютного прискорення точки.

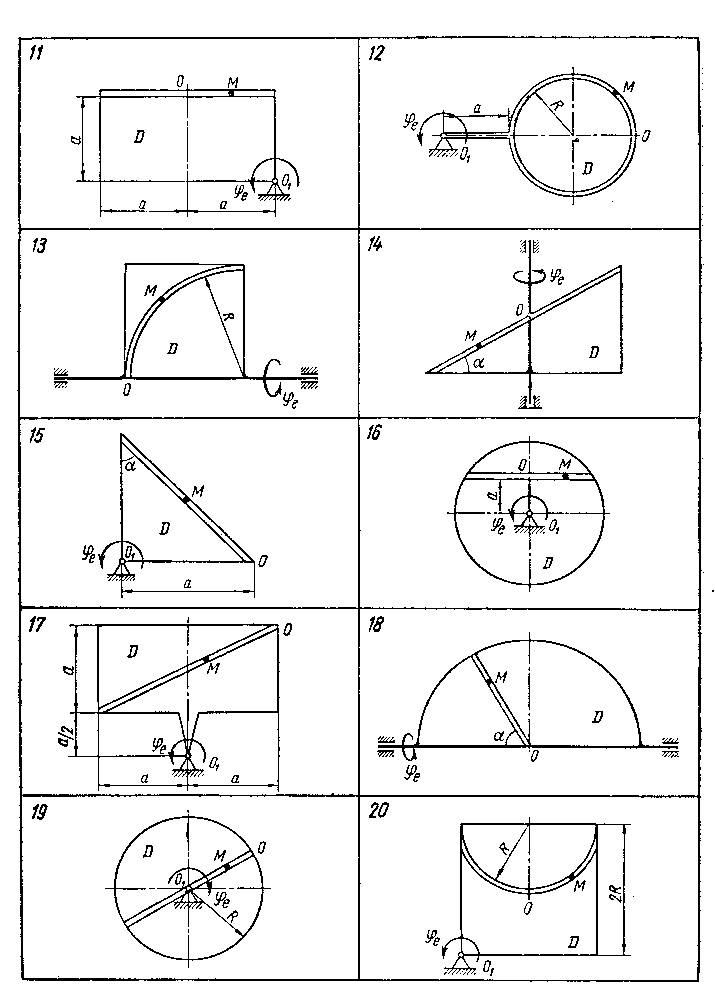
За данними рівняннями відносного руху точки М і переносного руху тіла Д визначити для момента часу t=t₁ абсолютну швидкість і абсолютне прискорення точки М, яка починає рухатися з точки О.

Схеми механізмів показані на рис. З, а необхідні дані наведені в таблиці 4 завдань, теорія в параграфах 1-4, а приклади в параграфі 5 глави 5 розділу 1 посібника.

Необхідно знати:

1. Основні визначення складного руху точки:

- абсолютний, відносний і переносний рухи;

- абсолютна , відносна і переносна швидкості точки;

- абсолютне , відносне , і переносне прискорення точки;

- прискорення Коріоліса .

2. Як визначається абсолютна швидкість точки.

3. Як визначається абсолютне прискорення точки.

4. Як визначається напрямок прискорення Коріоліса за правилом Жуковського.

Неохідно вміти:

1. Складний рух точки розкладати на відносний та переносний.

2. Брати похідні від простих функцій.

3. Знаходити напрямок прискорення Коріоліса.

4. Визначати вектор, що дорівнює геометричній сумі декількох векторів.

Таблиця 1

№ варіанта	Вид рівнянь руху	f1(t)	f2(t)	а1,см	b1,см	а2, см	b2,см	j, рад	t1, сек.
01 02 03	x=a1f1(t)+b1 y=a2f2(t)+b2	sin2j sin2j sin j	cos2j cos2j sin j	2 1 -10	4 8 5	3 1 2	5 -3 4	(П/8)t (П/12)t (П/6)t	2 4 2
04 05 06	x=a2f1(t)+b2 y=a1f2(t)+b1	sin2j2 sin2j2 sin j2	cos2j2 cos j2 sin j2	3 5 -1	1 2 6	1 5 3	2 3 -1	(П/18)t (ÖП/3)t (П/24)t	3 1 ½
07 08 09	x=a1f1(t)+b2 y=a2f2(t)+b1	j2 j j	j2 j j2	8 4 9	2 1 12	6 10 8	5 7 3	2t 3t2 t2	2 3 2
10 11 12	x=a2f1(t)+b1 y=a1f2(t)+b2	sin j sin j2 sin j	cos j cos j2 cos j	14 10 5	18 12 9	5 10 5	7 15 11	П/6t (Ö3/2П)t (3/5П)t	1 1/3 1/3
13 14 15	x=a1f2(t)+b1 y=a2f1(t)+b2	j2 j3 j3	j j j2	3 2 1	8 10 8	7 5 2	12 11 13	3t 5t 4t	3 2 1
16 17 18	x=b1f1(t)+a1 y=b2f2(t)+a2	sin2 j j3 sin 2j	sin2j j2 sin2j	2 5 9	12 7 11	4 12 7	14 15 12	(П/6)t 3t (П/10)t	2 0 ¼
19 20 21	x=b2f1(t)+a2 y=b1f2(t)+a1	cos2 j -sin j cos 2j	cos 2j -cos j -cos 2j	3 10 10	-10 -20 5	4 5 4	-5 4 -6	(П/12)t (П/8)t (П/16)t	4 4/3 2
22 23 24	x=b1f1(t)+a2 y=b2f2(t)+a1	sin2 j sin2 j2 j	cos 2j cos 2j2 j2	2 1 5	3 -6 3	1 1 7	7 -3 -9	(П/8)t (П/24)t 5t	4/5 4 2
25 26 27	x=b2f1(t)+a1 y=b1f2(t)+a2	sin 2j sin 2j2 j2	cos2 j cos2 j2 j3	9 1 2	-2 -4 12	5 2 3	-6 5 -2	(П/24)t2 (П/18)t t	2 3 2
28 29 30	x=b1f2(t)+a1 y=b2f1(t)+a2	cos2 j cos2 j2 sin 2j	sin2 j sin j2 cos 2j	3 1 2	-1 12 6	5 4 3	-4 -9 11	(П/9)t (П/4)t2 (П/12)t	6 1/2 4/9

Таблиця 2

№ варіанта	r2,см	R2, см	R3,см	S,м	Рівняння руху тягаря x=x(t), см
01 02 03	40 25 10	60 50 30	40 40 15	0,05 2,00 0,70	5+20t2 2+50t2 70t2
04 05 06	15 50 60	30 75 80	20 25 40	0,64 1,35 0,72	3+100t2 60t2 8+50t2
07 08 09	40 75 35	80 100 70	50 50 40	0,36 0,20 0,70	100t2 10+30t2 7+70t2
10 11 12	15 30 20	45 50 25	90 60 50	1,20 1,80 4,80	20+30t2 20t2 30t2
13 14 15	80 30 40	80 50 60	40 60 80	0,405 1,69 0,90	15+50t2 2+100t2 5+90t2
16 17 18	50 45 90	70 60 100	60 60 70	3,60 4,50 5,00	90t2 50t2 6+20t2
19 20 21	65 75 10	85 100 10	40 50 30	1,60 0,196 2.80	40t2 6+40t2 10+70t2
22 23 24	40 30 15	60 50 30	30 50 100	0,968 0,144 2,312	80t2 3+90t2 8+80t2
25 26 27	40 30 30	60 60 45	90 60 30	0,245 1,25 0,90	4+50t2 15+20t2 20+40t2
28 29 30	40 30 30	15 50 60	45 60 90	1,69 1,20 0,40	8+100t2 10+30t2 2+40t2

Таблиця 3

№ варианта	Розміри, см			wOA , рад/с	w1 , рад/с	eOA , рад/с2	VA , см/с	aA , см/с2
	ОА	r	AB
1	2	3	4	5	6	7	8	9
1	40	15	-	2	-	2	-	-
2	30	15	-	3	-	2	-	-
3	-	50	-	-	-	-	50	100
4	35	-	-	4	-	8	-	-
5	25	-	-	1	-	1	-	-
6	40	15	-	1	1	0	-	-
7	35	-	75	5	-	10	-	-
8	-	-	20	-	-	-	40	20
9	-	-	45	-	-	-	20	10
10	25	-	80	1	-	2	-	-
11	-	-	30	-	-	-	10	0
12	-	-	30	-	-	-	20	20
13	25	-	55	2	-	4	-	-
14	45	15	-	3	12	0	-	-
15	40	15	-	1	-	1	-	-
16	55	20	-	2	-	5	-	-
17	-	30	-	-	-	-	80	50
18	10	-	10	2	-	6	-	-
19	20	15	-	1	2,5	0	-	-
20	-	-	20	-	-	-	10	15
21	30	-	60	3	-	8	-	-
22	35	-	60	4	-	10	-	-
23	-	-	60	-	-	-	5	10
24	25	-	35	2	-	3	-	-
25	20	-	70	1	-	2	-	-
26	20	15	-	2	1,2	0	-	-
27	-	15	-	-	-	-	60	30
28	20	-	50	1	-	1	-	-
29	12	-	35	4	-	6	-	-
30	40	-	-	5	-	10	-	-

Таблиця 4

№ варіанта	R, см	а, см	a, град	Рівняння відносного руху точки М ОМ=Sr(t)	Рівняння руху тіла		t1, c
					jе=jе(t), рад	xе=xе(t), см
1	-	25	-	18sin(pt/4)	2t3-t2	-	0,5
2	20	-	-	20sin(pt)	0,5t2+1	-	1
3	-	30	-	6t3	2t+0,5t2	-	2
4	-	-	60	10sin(pt/6)	0,6t2	-	1
5	30	-	-	40pcos(pt/6)	3t-0,5t3	-	2
6	15	-	-	-	-	3t+0,3t3	3	jr=0,2pt3
7	-	40	60	20cos(2pt)	0,5t2	-	0,5
8	-	-	30	6(t+0,5t2)	t3-5t	-	2
9	-	-	-	10(1+sin2pt)	4t+1,5t2	-	0,3
10	20	20	-	20pcos(pt/4)	1,2t+t2	-	1,3
11	-	25	-	25sin(pt/3)	2t2-0,5t	-	4
12	30	30	-	15pt3/8	5t-4t2	-	2
13	40	-	-	120pt2	8t2-3t	-	0,25
14	-	-	30	3+14sin(pt)	4t-2t2	-	0,75
15	-	60	45	5(t2+t)	0,2t3+t	-	2
16	-	20	-	20sin(pt)	t-0,5t2	-	0,5
17	-	8	-	8t3+2t	0,5t2	-	1
18	-	-	60	8t3+2t	0,5t2	-	1
19	40	-	-	10t+t3	8t-t2	-	2
20	60	-	-	6t+4t3	t+3t2	-	2
21	25	-	-	3pcos(pt/6)	6t+t2	-	3
22	30	-	-	10psin(pt/4)	4t-0,2t2	-	0,75
23	18	-	-	6pt2	-	-	1	j=pt3/6 010=02A=20см
24	30	-	-	75p(0,1t+0,3t3)	2t-0,3t2	-	1
25	-	-	-	15sin(pt/3)	10t-0,1t2	-	5
26	-	-	45	8cos(pt/2)	-2pt2	-	0,75
27	75	-	-	-	-	50t2	2	jr=5pt3/48
28	40	-	-	2,5pt2	2t3-5t	-	2
29	30	-	-	5pt3/4	-	-	2	j=pt3/8 010=02A=40см
30	50	-	-	4pt2	-	t3+4t	2

Рис.1

Рис.2

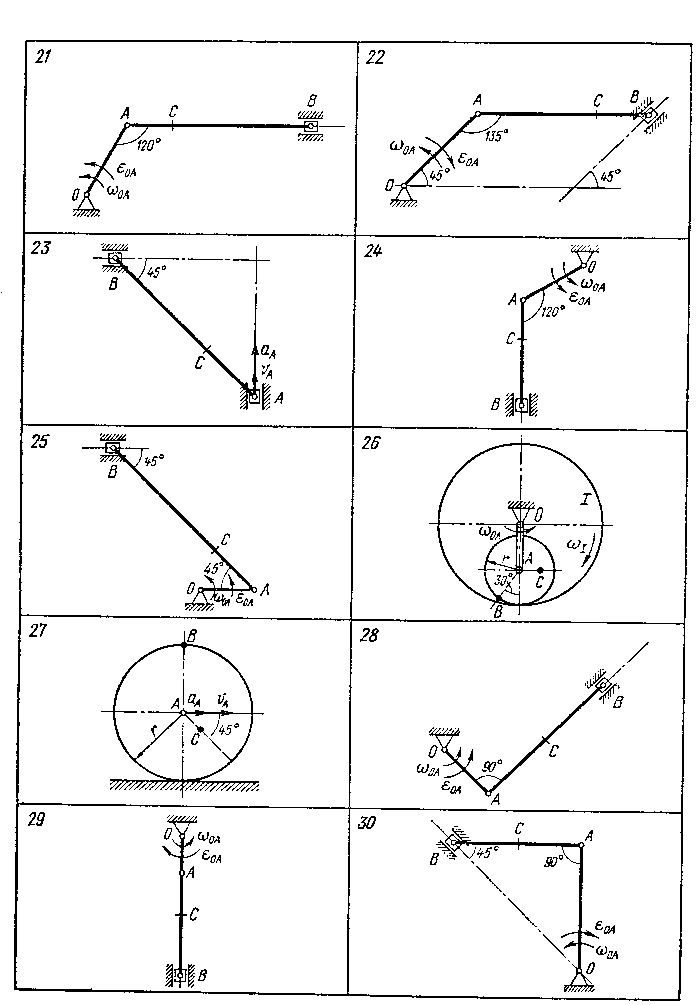
Рис.3