Ргр 3. Аналіз прямої

А. Теоретичні особливості

Проекції точки

Для графічного визначення або однозначного задання точки в декартовій системі координат необхідно задати не менше двох її проекцій. В загальному випадку точка задається трьома координатами X,Y,Z таким способом:

A(X,Y,Z).

Декартова просторова система координат утворена трьома безмежними площинами проекцій (рис. 3), де:

• ¹П – горизонтальна;

• ²П – фронтальна;

• ³П – профільна.

Ця система координат розділяє весь простір на вісім кутів – октантів, які

позначуються римськими цифрами. Перетин між собою площин проекцій дає координатні осі x,y,z.

Із аналізу побудов рис. 3 стає очевидною властивість наочного зображення просторової декартової системи координат: три взаємно перпендикулярні осі зображуються в площині рисунка під довільними кутами, а тому не можуть зображуватися в дійсну величину, оскільки їхні масштабні одиниці

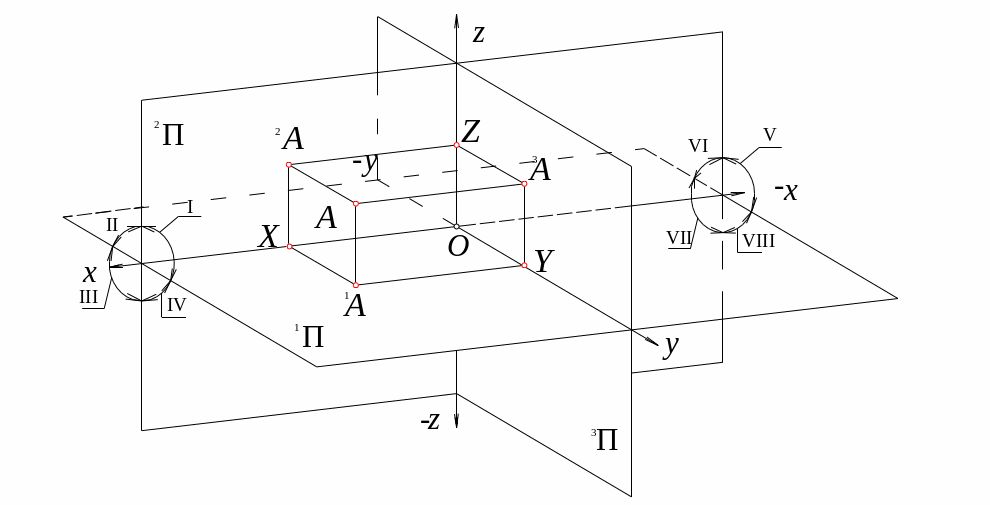
Рис. 3. Проекції точки А в декартовій системі координат

спотворені та різні за величиною. Така властивість наочного зображення

просторової системи координат створює значні труднощі при його використанні для об’єктів з реальними розмірами. Цього недоліку позбавлений епюр Монжа, в якому всі три площини проекцій суміщуються з площиною рисунка, як це показано на фрагментах рис. 4.

Рис. 4. Трансформація просторової системи координат а,в в епюр Монжа б, г, де:– б – епюр після суміщення площин ¹П і ²П;– г – епюр після суміщення площин ²П і ³П.

Висновки

Особливість епюра Монжа в тому, що на ньому існують дві осі у: одна для горизонтальної, а друга для профільної площин проекцій. Така особливість появляється внаслідок одночасних перетворень на рис. 4 б) та г), хоча в просторовій системі існує тільки одна вісь y !

Побудова третьої проекції точки за двома заданими

Побудова третьої проекції точки за двома відомими показана на

рис. 5.Точки знаходяться в октантах: А – в І–му; Б – в VII– му; В– в ІІ–му.

Рис. 5. Проекції точок

Властивості епюра Монжа

1. Горизонтальна та фронтальна проекції точок знаходяться на одній лінії зв’язку, перпендикулярній до осі x.

2. Фронтальна та профільна проекції точок знаходяться на лінії зв’язку, паралельній до осі x.

3. Для побудови профільної проекції точки координата Y з осі у горизонтальної проекції переноситься на вісь у профільної проекції (центр циркуля в точці О з радіусом ОY) завжди проти годинникової стрілки на 90⁰ (рис. 5).

Література: [1], стр. 11-14; [5], стр. 10-24.

Практична побудова проекцій точок та прямої

Для знаходження профільної проекції точки за заданими двома проекціями необхідно:

• через фронтальну проекцію точки провести лінію зв’язку, паралельну до осі x;

• через горизонтальну проекцію точки провести лінію зв’язку, паралельну осі x, до перетину з віссю y;

• перенести проти годинникової стрілки координату OY з осі y для горизонтальної площини проекцій на вісь y для профільної площини;

• через одержану точку провести перпендикулярну до осі y лінію зв’язку;

• перетин побудованих ліній зв’язку дає шукану профільну проекцію точки.

Наведений алгоритм дозволяє побудувати профільну проекцію точки, заданої як додатніми, так і від’ємними координатами (рис.5).

Пряма задається відрізками прямої або двома точками. Якщо пряма задається координатами двох точок А, В, то спочатку будують на епюрі проекції точок ¹А, ²А, ¹В, ²В, за якими знаходять профільні проекції точок (рис.3). З’єднуючи відповідні проекції точок, одержують аналогічні проекції прямої а.

Пряма. Відображення прямої

Пряма задається графічно відрізком або двома точками (рис. 6).

Точка належить до прямої, якщо її проекції розташовані на відповідних проекціях прямої (рис. 6).

Рис. 6. Задання прямої. Належність точки В до прямої

Розташування прямої відносно площин проекцій

Властивості прямої залежать від її розташування відносно площин проекцій.

Пряма загального положення

Така пряма не паралельна і не перпендикулярна ні до однієї із площин проекцій (рис. 6).

Пряма рівня

Пряма рівня паралельна до однієї з площин проекцій (рис. 7).

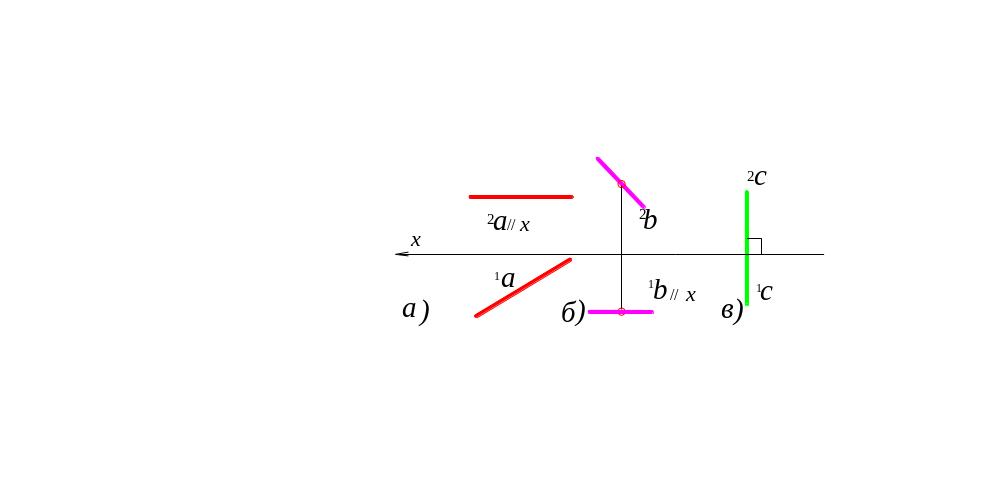
Рис. 7. Прямі рівня: а//¹П; b//²П; с//³П: а –горизонтальна пряма; b –фронтальна пряма; с –профільна пряма

Пряма проектуюча

Проектуюча пряма перпендикулярна до однієї із площин проекції (рис. 8), де l┴¹П; с┴²П; q┴³П.

Рис. 8. Проектуючі прямі: l – горизонтально–проектуюча;

с – фронтально–проектуюча; q – профільно–проектуюча

Висновки

Особливості проектуючи прямих та прямих рівня використовуються для спрощення розв’язків задач.

Сліди прямої

Слідами прямої називаються точки її перетину з площинами проекцій, при цьому:

– H –горизонтальний слід, наприклад H_а =а∩¹П, тобто точка перетину прямої а з горизонтальною площиною;

– F –фронтальний слід, наприклад F_а =а∩²П, тобто точка перетину прямої а з фронтальною площиною;

– P –профільний слід, наприклад Р_а =а∩³П, тобто точка перетину прямої а з профільною площиною.

Сліди прямої, як і будь–які точки, можна відобразити трьома проекціями.

Рис. 9. Сліди прямої а в просторовій системі координат

Основні особливості слідів прямої:

–співпадання (тотожність) сліда із однією своєю ж проекцією, тобто Н¹Н, F²F, Р³P, що виникає внаслідок належності сліда до площини проекції;

–на відповідних проекціях прямої знаходяться проекції слідів із такими ж індексам.

На рис. 9 штриховими лініями зображено невидимі, закриті площинами проекцій, дільниці прямої а. Ця ж пряма а із слідами зображена на епюрі Монжа (рис. 10), де зберігаються описані вище властивості слідів. Римськими цифрами показані кути простору, через які проходять дільниці такої прямої.

Рис. 10. Сліди прямої та кути простору, через які вона проходить

Рис. 11. Сліди профільної прямої

Проекції слідів прямої будуються за правилами побудови проекцій звичайних точок, використовуючи додаткові умови, тобто:

• перетин фронтальної проекції прямої з віссю x дає фронтальну проекцію горизонтального сліду ²Н, а перетин цієї ж проекції прямої з віссю z – фронтальну проекцію профільного сліду ²Р;

• перетин горизонтальної проекції прямої з віссю x дає горизонтальну проекцію фронтального сліду ¹F, а перетин цієї ж проекції прямої з віссю у – горизонтальну проекцію профільного сліду ¹Р;

• горизонтальна проекція горизонтального сліду ¹Н знаходиться лінією зв’язку 1 на фронтальній проекції прямої;

• фронтальна проекція фронтального сліду ²F знаходиться лінією зв’язку 2 на фронтальній проекції прямої;

• інші проекції слідів знаходяться звичайним способом за відомими двома проекціями.

Для профільної прямої рівня межі октантів вказуються лініями, паралельними до осі z. Така пряма може мати тільки горизонтальний та фронтальний сліди (рис. 11).

Необхідно запамятати:

Горизонтальна проекція фронтального сліду ¹F_a є точкою перетину горизонтальної проекції прямої ¹а з віссю х , а фронтальна проекція ²F_а належить до фронтальної проекції прямої ²а.

Фронтальна проекція горизонтального сліду ²Н_а є точкою перетину фронтальної проекції прямої ²а з віссю х, а горизонтальна проекція ¹Н_а належить до горизонтальної проекції прямої ¹а.

Горизонтальна проекція профільного сліду ¹Р_а є точкою перетину горизонтальної проекції прямої ¹а з віссю y.

Фронтальна проекція профільного сліду ²Р_а є точкою перетину фронтальної проекції прямої ²а з вісю z.

Висновки

Сліди прямої використовуються в задачах на належність прямої до площини.