Контрольна робота №2 Зразок розв`язання і оформлення контрольної роботи №2

Варіант № 31

Завдання 2.1.31. а) Знайти невизначений інтеграл

Розв’язання. Для знаходження інтеграла застосуємо формулу заміни змінної для невизначеного інтеграла , а саме:

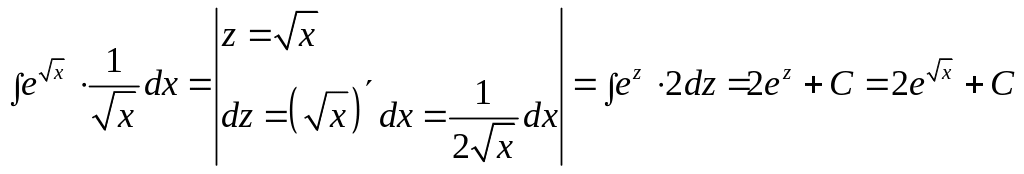
Таким чином,

;

б) знайти невизначений інтеграл

.

Розв’язання. Для знаходження інтеграла застосуємо формулу інтегрування частинами.

Використовуючи зауваження до неї, тобто позначаючи через обернену тригонометричну функцію

Таким чином,

;

в) обчислити невизначений інтеграл

.

Розв’язання. В цьому прикладі підінтегральна функція є правильною раціональною функцією. Розкладемо знаменник дробу на добуток лінійного множника та неповного квадрата різниці

.

Далі розкладаємо підінтегральну функцію на два доданки з невизначеними поки що коефіцієнтами

(1)

Для визначення коефіцієнтів А, В, С праву частину рівності (1) зводимо до спільного знаменника і групуємо члени чисельника

Прирівнюючи коефіцієнти при однакових степенях у правій і лівій частинах чисельників дробів, дістанемо систему лінійних рівнянь відносно невідомих коефіцієнтів :

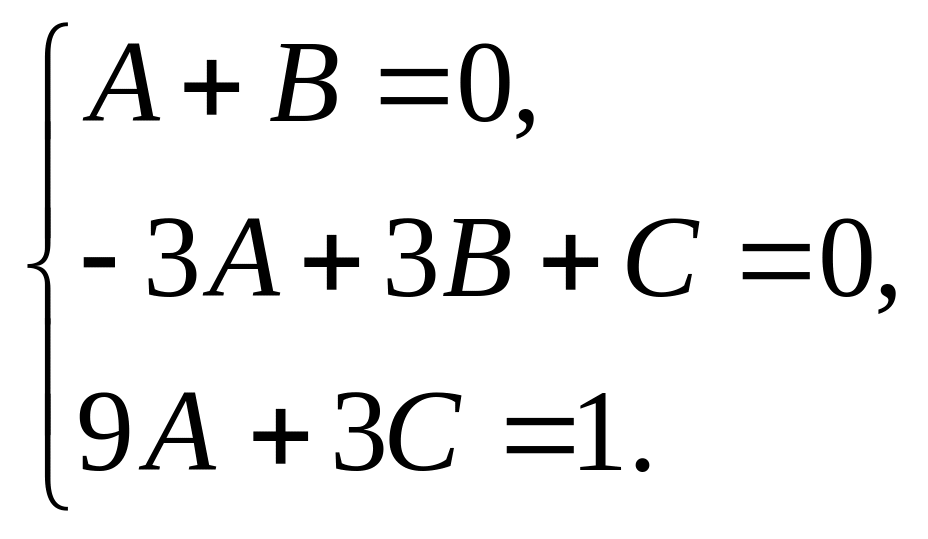
Розв’язок цієї системи такий:

Таким чином, підінтегральна функція дорівнює

і

.

Кожний з інтегралів обчислюємо окремо.

1. тому, що підінтегральній функції в чисельнику міститься точна похідна знаменника.

2.

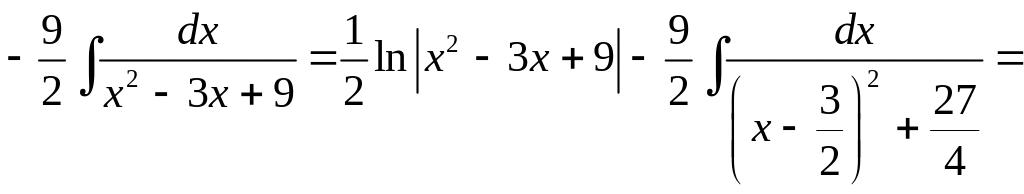
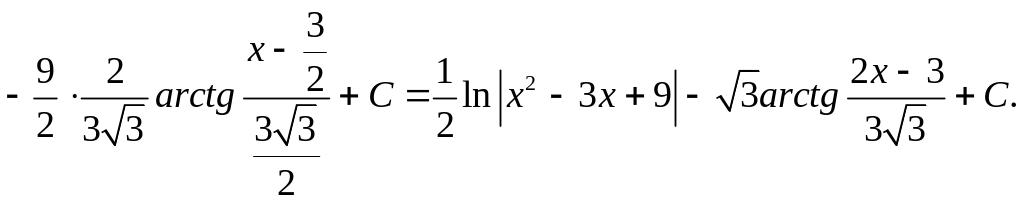
Таким чином,

;

г) обчислити невизначений інтеграл

^.

Розв’язання. В цьому інтегралі підінтегральна функція є ірраціональною і тому для перетворення цього інтеграла в інтеграл від раціональної функції зробимо таку заміну:

(де =Н.С.К. (2) = 2).

Таким чином,

.

;

;

д) обчислити невизначений інтеграл

.

Розв’язання. Підінтегральна функція є тригонометричною, а саме, раціональною від . Такі інтеграли беруться за допомогою універсальної тригонометричної підстановки

:

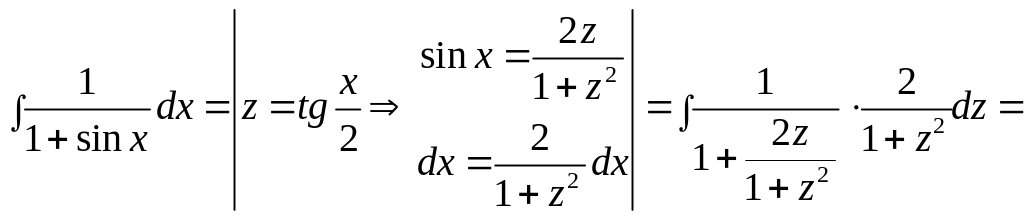
Таким чином,

.

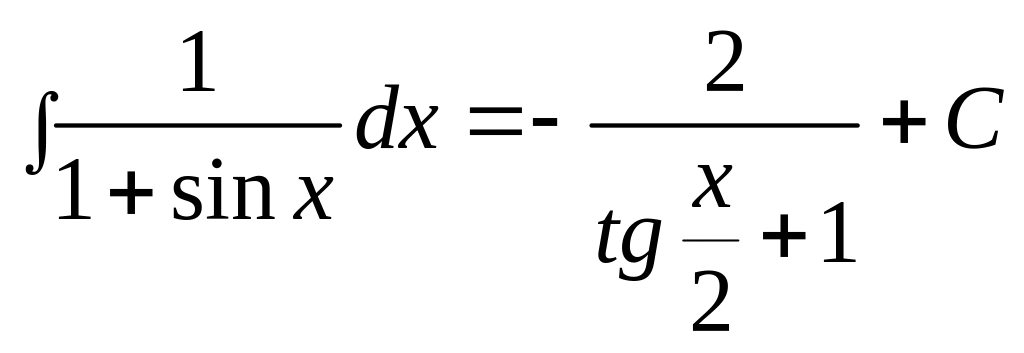е) обчислити невизначений інтеграл .

Розв’язання. Застосуємо підстановку , тоді отримаємо:

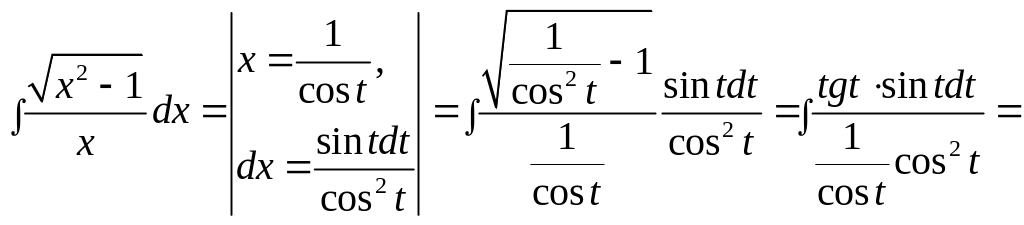
Таким чином,

.

Завдання 2.2.31.

а) Обчислити визначений інтеграл .

Розв’язання.

Застосуємо спочатку формулу заміни змінної під знаком визначеного інтеграла

Таким чином,

б) Обчислити визначений інтеграл

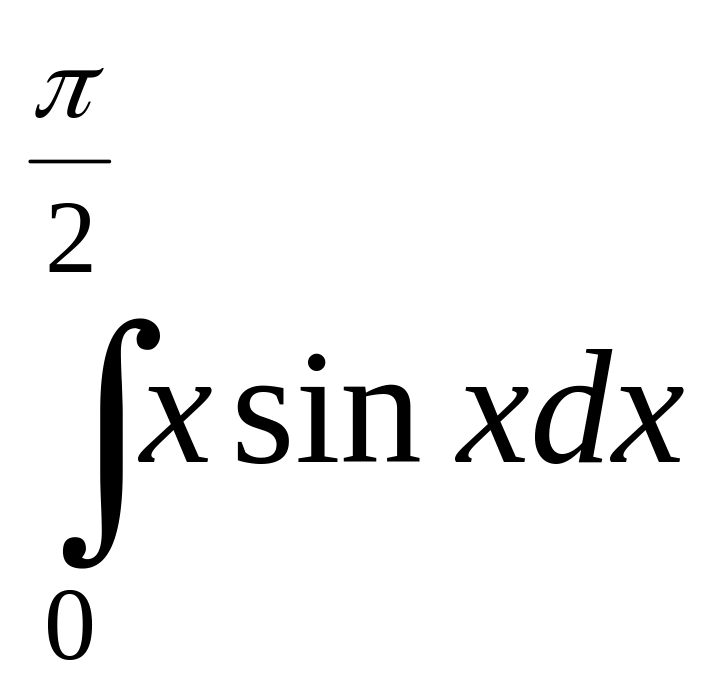
Розв’язання.

Застосуємо спочатку формулу інтегрування частинами, тому що підінтегральна функція є добутком степеневої функції і тригонометричної

.

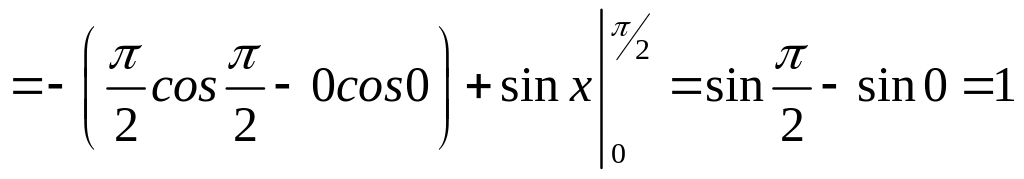Таким чином,

.

Завдання 2.3.31. Обчислити площу фігури, обмеженої лініями .

Розв’язання. По-перше, в системі координат ХОУ зробимо рисунок фігури, для чого за даними рівняннями нарисуємо відповідні лінії: - парабола, - пряма.

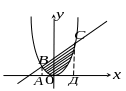
Між параболою і прямою утворюється фігура, яку можна розглядати як різницю двох криволінійних трапецій АВСД і АВОСД.

Основою обох трапецій є відрізок початок А і кінець Д якого є абсцисами точок перетину параболи і прямої. Знайдемо абсциси точок перетину даних ліній. Розв’язуючи систему рівнянь, знаходимо межі інтегрування.

.

Знаходимо площу

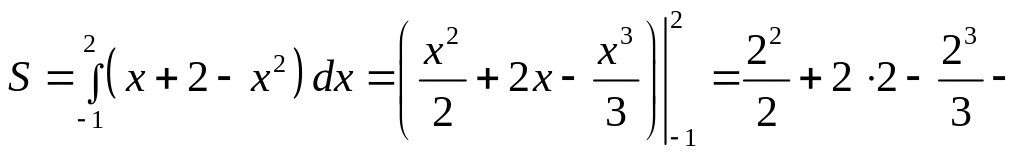
Таким чином,

кв. од.

Завдання 2.4.31. Знайти розв’язок задачі Коші лінійного диференціального рівняння першого порядку

.

Розв’язання. Задача Коші полягає в тому, щоб визначити частинний розв’язок диференціального рівняння, використовуючи для цього початкову умову. Для цього спочатку знаходимо загальний розв’язок диференціального рівняння.

Задане рівняння є лінійним ( і містяться в рівнянні лише в перших степенях). Розв’язуємо його методом Бернуллі. За формулою маємо

, .

, .

Складаємо систему двох рівнянь:

Розв’язуємо перше з рівнянь системи:

, .

Підставляємо отримане значення функції в друге рівняння системи і розв’язуємо його:

, .

Запишемо загальний розв’язок диференціального рівняння

.

Для розв’язання задачі Коші застосуємо початкову умову і знайдемо значення сталої , для чого підставимо в загальний розв’язок значення , :

.

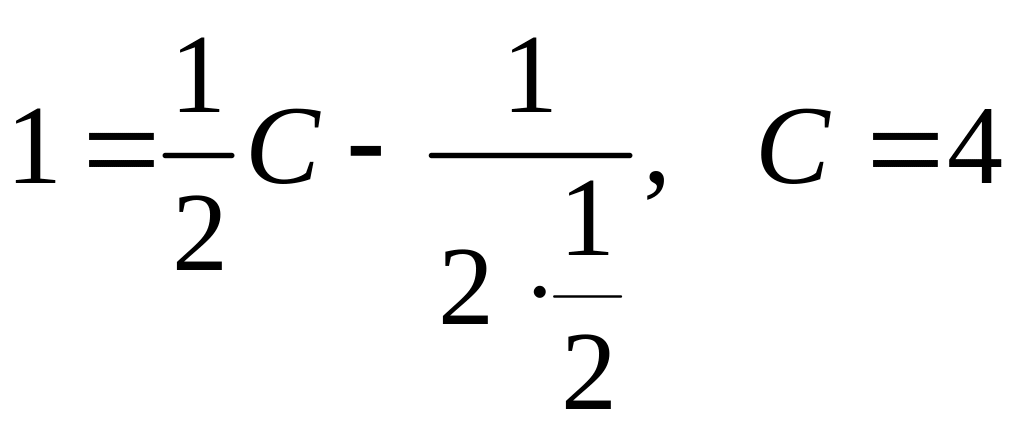Отже, частинний розв’язок диференціального рівняння має вигляд

.