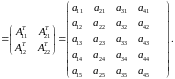2.4. Блочные матрицы.
Если
разделить некоторую матрицу А на части
вертикальными и горизонтальными прямыми,
то получаются прямоугольные ячейки,
являющиеся сами по себе матрицами. Эти
ячейки называются блоками
матрицы.
Сама матрица А может рассматриваться
как таблица, элементами которой являются
более мелкие таблицы
:
.
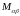При таком построении матрица А составляется
из блоков и поэтому называется блочной.
Например, матрицу
разобьем на следующие блоки
и обозначим их
,
,
,
.
Тогда матрицу А можно записать в виде блочной матрицы, элементами которой будут эти матрицы :
.
Матрицу А на блоки можно разбить иным способом
.
Тогда блоками матрицы будут
,
,
,
,
,
,
,
,
.
Тогда блочная матрица А будет иметь вид
.
Нетрудно
видеть, что для
составления блочной матрицы из серии
матриц
( блоков) необходимо, чтобы подмножества
матриц с одинаковыми значениями индекса
имели одинаковое количество строк, а
подмножества матриц с одинаковым
значением индекса
– одинаковое значение столбцов.
Пример. Указанным требованиям удовлетворяют следующие четыре матрицы:
,
,
,
.
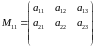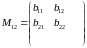Поэтому из них можно составить блочную матрицу
.
Основное свойство блочной матрицы состоит в том, что операции над блочными матрицами совершаются по тем же правилам, что и операции над обычными матрицами.
При сложении блочных матриц: размеры слагаемых блочных матриц должны быть одинаковы; размеры отдельных блоков с равными индексами у слагаемых матриц должны бать одинаковы.
Умножение блочных матриц.
Пусть
блочные матрицы
и
удовлетворяют двум условиям
1. Число «блочных» столбцов матрицы А совпадает с числом «блочных» строк матрицы В (т.е. индекс для А и В изменяется в одинаковых пределах). Или иначе: длина блочной строки матрицы А равна высоте блочного столбца матрицы В.
Например
-
размер 2×3,
-
размер 3×3.
2.
Для любых
число столбцов у матрицы – блока
совпадает с числом строк у матрицы –
блока
.
Например:
,
.
Тогда
,
.
Принцип умножения такой же как и для обычных матриц: блочная строка матрицы А умножается на блочный столбец матрицы В.
Если блоки матриц – квадратные матрицы одного порядка, то условие упрощается: число блочных столбцов множимого должно совпадать с числом блочных строк множителя.
Представление матриц в блочном виде часто оказывается удобным при нахождении суммы и произведения, если матрицы имеют достаточно большой размер, а их согласованные разбиения на блоки содержат нулевые, единичные, диагональные, треугольные матрицы.
Пример. Найдем произведение блочных матриц, предполагая, что все операции определены:
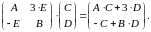
Транспонирование блочной матрицы.
При транспонировании блочной матрицы транспонированию подлежат и ее элементы.
Пример:
.
Транспонируем блочную матрицу
