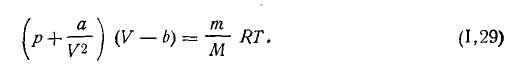§ 3. Молекулярно-кинетическая теория газов.

Основы молекулярно-кинетической теории газов, которая объ­яснила физический смысл газовых законов, были заложены еще в работах М. В. Ломоносова. В 1744—1748 гг. он разработал теорию атомно-молекулярного строения вещества, впервые обосновал ки­нетическую теорию теплоты и на основании этого объяснил мно­гие неизвестные до него явления. В XIX в. молекулярно-кинетиче­ская теория газов получила свое дальнейшее развитие в работах Клаузиуса, Максвелла и Больцмана. На новейшем ее этапе эта теория была в современном виде разработана Я. И. Френкелем.

В основе кинетической теории идеальных газов лежат следую­щие простые допущения.

Каждый газ

1) состоит из молекул, которые можно рассматри­вать как однородные абсолютно упругие шарики; причем размеры этих шариков-молекул настолько малы по сравнению с межмоле­кулярными расстояниями, что их можно рассматривать как от­дельные материальные точки;

2) столкновение молекул между собой подчиняется законам уда­ра упругих шаров;

3)молекулы не взаимодействуют друг с другом, пока не столк­нутся;

4)движение молекул в газе хаотично, непрерывно, поступа­тельно.

Молекула в разные моменты времени обладает самыми разно­образными скоростями как по величине, так и по направлению. Поэтому трудно описать движение отдельной молекулы. Однако в целом к огромному количеству молекул вследствие беспорядочно­сти их движения можно при­менять законы теории вероят­ности.

Известно, что при множест­ве движущихся молекул (или атомов) число частиц, облада­ющих скоростью, лежащей в данном интервале значений, остается постоянным. Теорети­ческие подсчеты, произведен­ные Максвеллом в 1860 г., по­казали, что молекулы газа по скоростям движения при дан­ной температуре распределя­ются строго определенным об­разом.

Молекулярно-кинетическая теория объяснила многие свойства газов, например стремление их занять возможно больший объем, давление на стенки сосуда, медленный характер процесса диффу­зии, рост давления с повышением температуры и др.

Молекулы ударяются о стенки сосуда, создавая тем самым дав­ление. Его мерой является сила ударов движущихся молекул о по­верхность в 1 м² в 1 с. С повышением температуры скорость движе­ния молекул увеличивается, вместе с тем увеличивается и число ударов молекул о стенки сосуда, т. е. растет давление газа.

В каждый отдельный момент молекула имеет разные скорости как по величине, так и по направлению, но для каждой постоянной средняя скорость движения молекул есть величина постоянная.

Применяя к хаотическому движению молекул в газе законы меха­ники, удалось получить основное уравнение, которое связывает объем и давление со средней квадратичной скоростью движения молекул газа:

1.23

где N — число молекул газа, находящихся в объеме V; m — масса одной молекулы данного газа.

Для 1 кмоль газа можно записать основное уравнение

1.24

где N₀ — постоянная Авогадро. Уравнение (I.24) называется основ­ным, потому что из него можно математически вывести все рас­смотренные выше законы идеальных газов, рассчитать кинетиче­скую энергию молекулы, среднюю скорость движения молекул газа и ряд других важных следствий.

Пользуясь основным уравнением (I.24), можно вывести простое соотношение, чтобы вычислить средние квадратичные скорости движения молекул различных газов для разных температур. При этом необходимо заменить произведение N₀m равной ему молярной массой М: pV= ^l/₃ Mu²,но РV= RT; RT= ^l/₃Mu², откуда

1.25

Из уравнения (I.25) следует, что средняя квадратичная скорость зависит от температуры и природы газа. Для данного газа при по­стоянной температуре является величиной постоянной и выража­ется в м/с. Так, для водорода, азота и кислорода средние квадра­тичные скорости молекул при 0° С соответственно равны 1845, 493 и 461 м/с.

Для реальных газов уравнение Ван-дер-Ваальса будет

1.26

Уравнение Ван-дер-Ваальса значительно точнее отображает состояние реального газа, чем уравнение (I.17), которое было вы­ведено для идеальных газов.