1.2. Геометрична інтерпретація злп. Графічний метод розв’язування

Для того, щоб краще зрозуміти суть розв’язування ЗЛП, яка записана в симетричній формі, з’ясуємо геометричний зміст системи лінійних нерівностей з двома невідомими.

Визначення 1.4. Множина називається опуклою, якщо вона разом з точками і містить всі точки х відрізка , тобто точки виду .

Розглянемо спочатку одну лінійну нерівність з двома невідомими і : , яка визначає одну з півплощин, тобто справджується в точках однієї з півплощин, на які пряма ділить координатну площину, і не справджується в точках іншої (пряма відноситься до кожної з півплощин). В цьому випадку кажуть, що дані нерівності визначають замкнену півплощину. В свою чергу, нерівності ( ) визначають відкриту півплощину.

Для визначення конкретної півплощини вибираємо довільну точку і перевіряємо чи правильна нерівність. Для зручності вибираємо , якщо вона не належить граничній прямій. Якщо нерівність справджується, то розв’язком буде та півплощина, яка містить вибрану точку, в іншому випадку – яка його не містить.

Наприклад, розв’язком нерівності буде замкнена півплощина (рис.1.2), яка містить початок координат, а розв’язком нерівності буде відкрита півплощина (рис.1.3), яка його не містить.

Рис.1.2

Рис.1.3

В першому випадку шукана півплощина лежить нижче прямої а в другому – вище прямої .

В найпростішому випадку система лінійних нерівностей з двома невідомими складається з двох нерівностей

Ця система називається сумісною, якщо існують такі числові значення невідомих і , які одночасно задовольняють обидві нерівності. Геометрично система сумісна, якщо в площині O існують точки, координати яких задовольняють обидві нерівності. Якщо таких точок нема, то система нерівностей називається несумісною.

Н а рисунку 1.4 показано внутрішню частину кута АВС, координати всіх точок якого є розв’язками системи нерівностей крім точок, що належать прямій ВС.

Рис.1.4

В свою чергу, розв’язком системи нерівностей 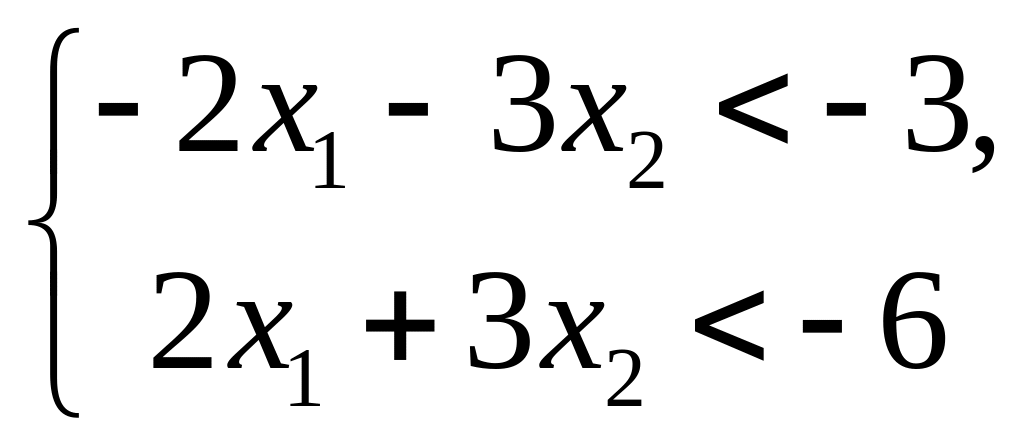буде порожня множина. Дійсно, переписавши систему у вигляді бачимо, що нерівності суперечливі між собою (рис.1.5).

Рис. 1.5

Припустимо тепер, що задана деяка система лінійних нерівностей з невідомими і :

(1.2)

Сукупність розв’язків кожної з нерівностей цієї системи геометрично зображається множиною точок деякої півплощини, а сукупність всіх розв’язків системи (1.2) представляє собою деяку множину точок перетину (спільну частину) цих півплощин, границя якої складається з відрізків відповідних прямих.

Оскільки півплощина є опуклою множиною, то і множина розв’язків теж є опуклою. Назвемо її многокутною областю. Її також називають областю розв’язків системи нерівностей (1.2), або многокутником розв’язків. Зауважимо, що область розв’язків може бути многокутником, нескінченною множиною, смугою, що міститься між двома паралельними прямими, прямою, променем, відрізком, точкою, або порожньою множиною.

Приклад 1.2. Побудувати многокутник розв’язків системи нерівностей:

Розв’язок. Записуємо рівняння граничних прямих , і будуємо їх на площині. Візьмемо і визначаємо півплощини, які відповідають першим двом нерівностям системи. Взявши до уваги також нерівності , дістанемо опуклий многокутник ОАВС, який є многокутником розв’язків заданої системи нерівностей (рис.1.6)

Рис.1.6

Враховуючи вищенаведені зауваження, переходимо до розв’язування прикладу 1.1.

Записуємо рівняння граничних прямих: і будуємо їх на площинні.

Підставляючи в кожну нерівність системи (1.1) і , визначаємо півплощини, які відповідають вихідним обмеженням-нерівностям.

Враховуючи умови невід’ємності, отримаємо, що перетин (спільна частина) розглянутих півплощин представляє собою многокутник ОАВСD (рис.1.7)

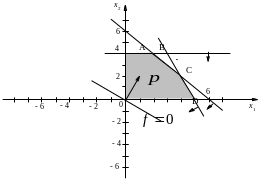
Рис.1.7

Будуємо вектор , координати якого рівні коефіцієнтам при і в цільовій функції, і перпендикулярно до нього пряму . Для визначення екстремальної точки переміщаємо пряму в напрямку вектора паралельно самій собі. Найбільш віддаленою точкою, в якій пряма зустрінеться з областю допустимих розв’язків , буде точка В, яка є точкою перетину прямих і . Координати точки В є розв’язками наступної системи рівнянь . Тоді .

Отже, максимальна сума, отримана від реалізації прикрас, дорівнює 10 тис.грн. З них: (тис.грн.) від реалізації прикрас виду і (тис.грн.) від реалізації прикрас виду .

Цей метод розв’язування називається графічним і використовується для випадку, коли кількість невідомих , або коли , де – число змінних задачі, а – ранг матриці системи обмежень. У випадку вже немає такої наглядної інтерпретації.

Сформулюємо тепер ЗЛП з двома змінними і вкажемо алгоритм її розв’язування.

Отже, ЗЛП в симетричній формі формулюється так: знайти найбільше значення функції

(1.3)

при обмеженнях

(1.4)

. (1.5)

Як зазначалося вище, область розв’язків задачі (1.3) – (1.5) може бути многокутником, нескінченною областю, смугою, що міститься між двома паралельними прямими, точкою або порожньою множиною.

Функція (1.3) представляє собою на площинні сім’ю паралельних прямих, кожній з яких відповідає певне значення . Перпендикулярний до цих прямих вектор вказує напрямок найшвидшого зростання функції (рис.1.9) і ЗЛП (1.3) – (1.5) полягає в наступному: необхідно знайти точку допустимих значень, через яку проходить пряма сім’ї функцій , і в якій функція приймає найбільше значення (рис.1.9). При розв’язуванні ЗЛП графічним методом може трапитись, що задача (1.3) – (1.5) має:

• єдиний розв’язок – координати точки А (рис.1.10.a);

• нескінченну множину розв’язків – координати будь-якої точки, що належить відрізку АВ (рис.1.10.б);

• функція не досягає екстремального значення – 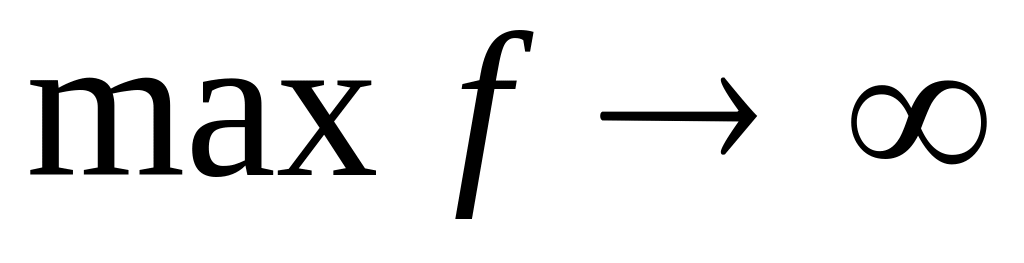(рис.1.10.в).

а) б)

в) г)

Рис. 1.8

Рис.1.9

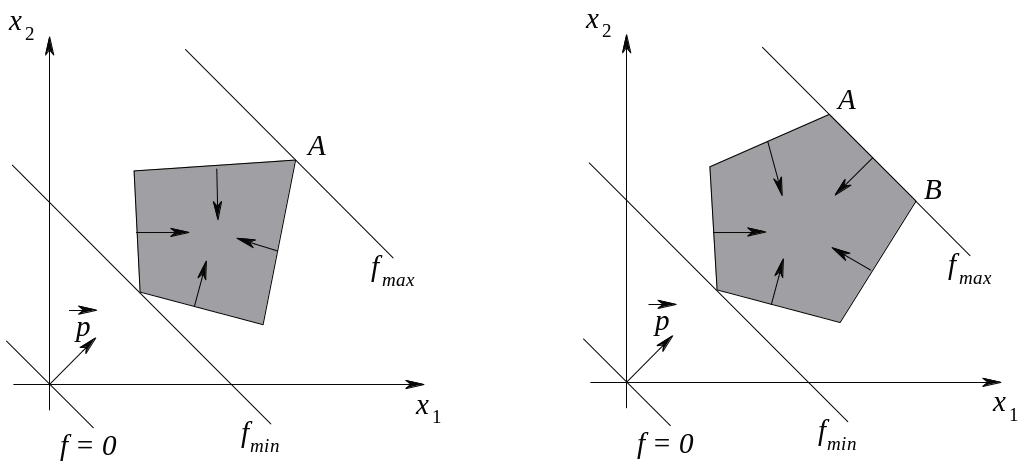
а) б)

в)

Рис.1.10

Розв’язування ЗЛП графічним методом проводиться в наступній послідовності:

1. записують рівняння граничних прямих і будують їх на площинні ;

2. визначають півплощину, яка відповідає вихідним обмеженням-нерівностям. Для цього беруть будь-яку точку і її координати підставляють в ліву частину обмеження-нерівності. Якщо вона при цьому перетворюється в правильну, то шуканою буде півплощина, яка містить цю точку, якщо ні, то шуканою буде півплощина, якій дана точка не належить;

3. виділяють область допустимих розв’язків задачі як спільну частину 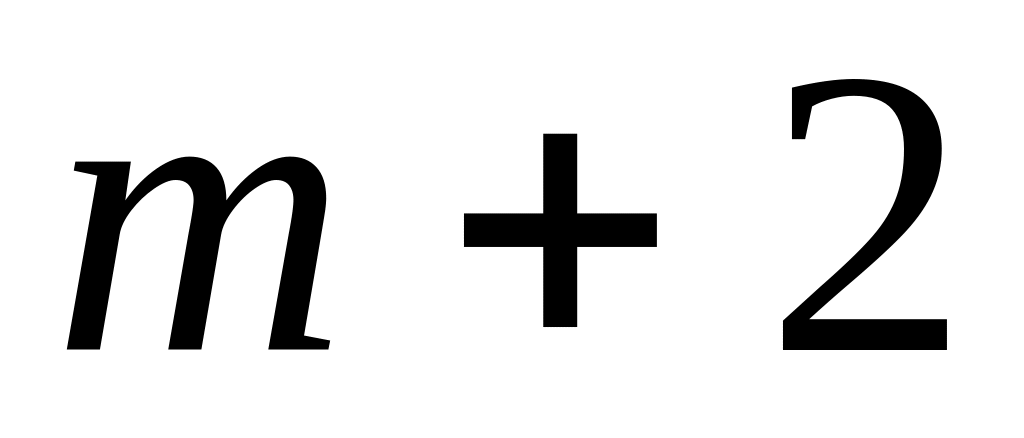півплощин, де півплощин відповідають вихідним нерівностям (1.4), а дві півплощини – умові невід’ємності змінних і ;

4. будують вектор і перпендикулярно до нього одну із прямих сім’ї функцій , наприклад, ;

5. визначаємо точку екстремуму на многокутнику розв’язків шляхом паралельного переміщення допоміжної прямої в напрямку вектора . Це буде найбільш віддалена крайня точка, в якій пряма зустрінеться з областю допустимих розв’язків. Якщо необхідно знайти точку, якій відповідає мінімальне значення функції , то лінію рівня переміщаємо в напрямку вектора до перетину з першою точкою допустимої області (або пряму в напрямку вектора ;

6. знаходимо координати точки екстремуму і значення функції в цій точці.