4.3 Основний принцип утворення механізмів

Основний принцип утворення механізмів полягає у тому, що будь-який механізм можна одержа­ти, якщо до початкової ланки (або початкових ланок) і стояка послідовно приєднувати кінематичні ланцюги з нульовим ступенем вільності.

Відомо, що до складу кожного ме­ханізму входять нерухома ланка (стояк), початкові ланки, тобто ланки, закони руху яких задано і від яких залежать закони руху всіх інших ланок. Отже, приступаючи до створення механізму необхідного ступеня вільності, закріпляємо одну з ланок (утво­рюємо стояк) і вводимо до кінематичної пари з цією ланкою по­чаткові ланки за кількістю ступенів вільності, які повинен мати механізм. При цьому кожна початкова ланка повинна мати тільки один ступінь вільності.

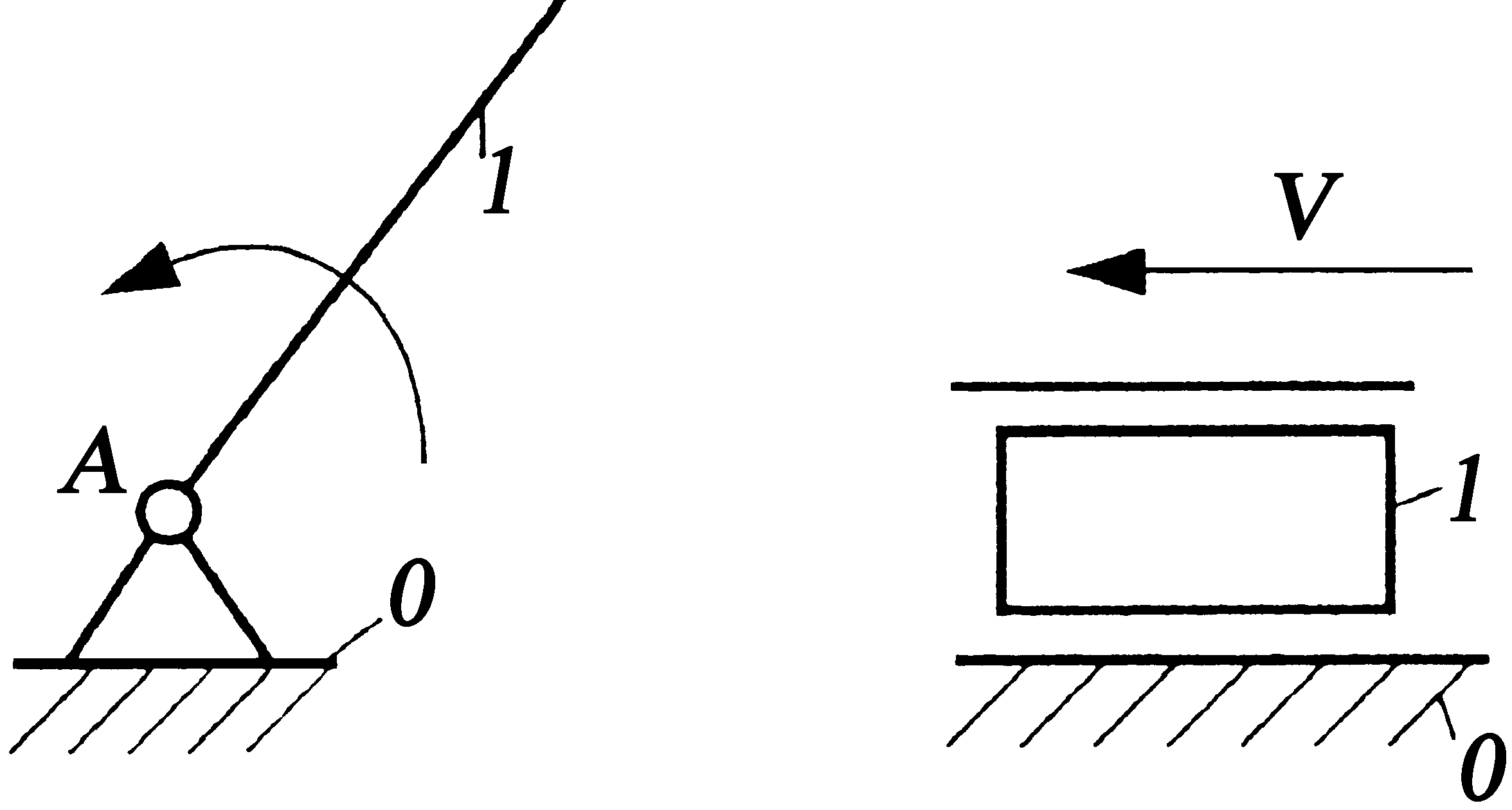
а) б) Рисунок 4.9 – Механізми I класу

Назвемо умовно початкову ланку і стояк, що утворюють кінематичну пару V класу, механізмом І класу. На рисунку 4.9 наведені механізми І класу, початкові ланки яких утворюють із стояком обертову або поступальну пару. Щоб одержати механізм потрібного ступеня вільності, не­обхідно до механізму (механізмів) І класу приєднати систему ланок, яка становить один або кілька кінематичних ланцюгів з нульовим ступенем вільності. Остання умова випливає з того, що весь механізм повинен мати ступінь вільності, який дорівнює сумі ступенів вільності механізмів І класу.

Як приклад, розглянемо плоский механізм, наведений на рисунку 4.10. Ступінь вільності цього механізму можна визначити за формулою Чебишова:

W = 3n – 2p₅ – p₄ = 3  5 – 2  7 – 0 = 1,

де число рухомих ланок n = 5, число кінематичних пар V класу р₅ = 7 і число кінематичних пар IV класу р₄ = 0.

Якщо прийняти стояк 0 і ланку 1 за механізм І класу (рисунок 4.10,б), то ланки 25 утворюють систему ланок, що ма­ють нульовий ступінь вільності (n= 4, р₅ = 6).

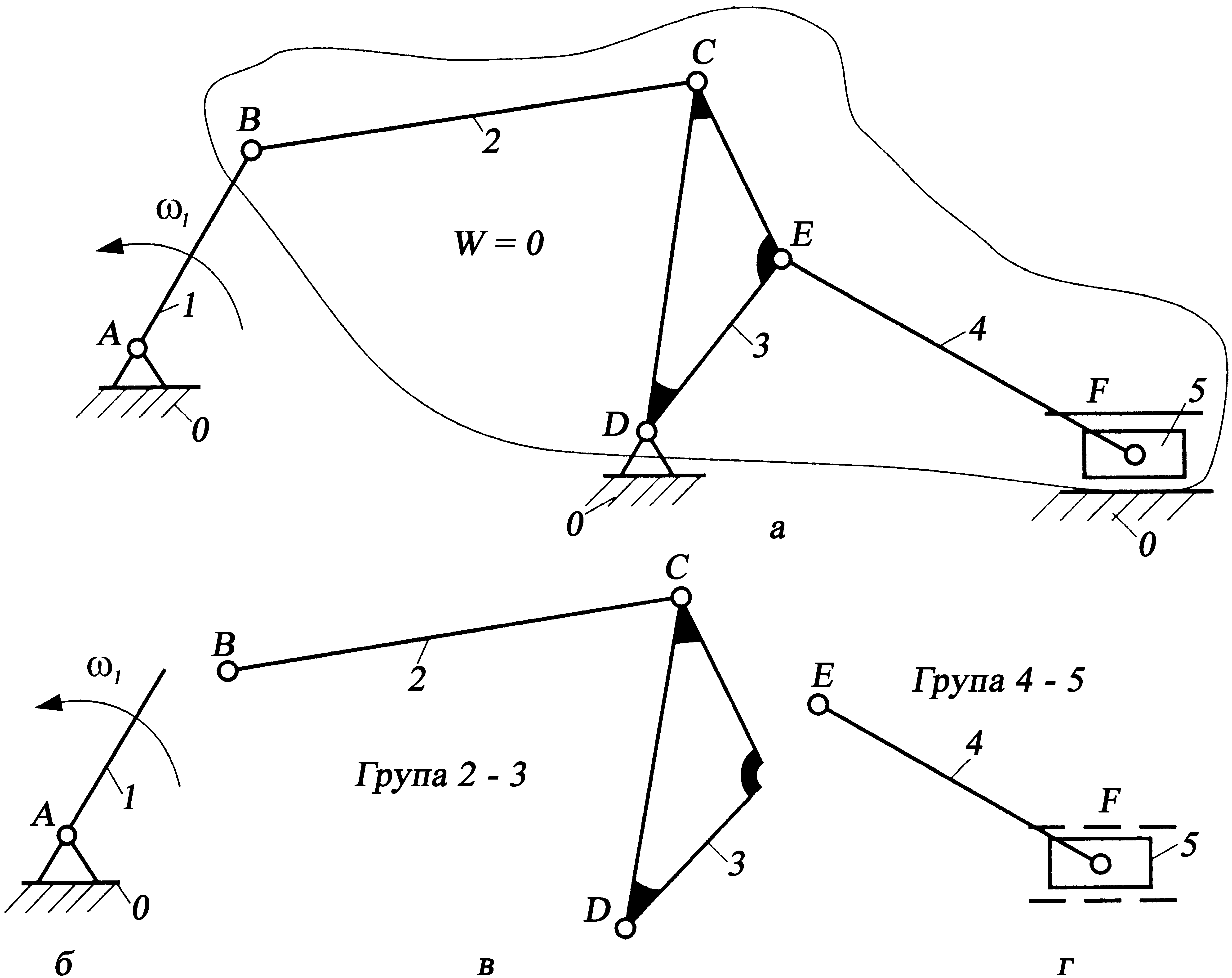
Рисунок 4.10 – Плоский механізм із ступенем вільності W = 1

Неважко побачити, що кіне­матичний ланцюг з ланок 25 можна поділити на два кінема­тичні ланцюги: один, складений з ланок 23 (рисунок 4.10, в), і другий, складений з ланок 45 (рисунок 4.10, г). Кожний з цих кінематичних лан­цюгів, складений з двох ланок і трьох кінематичних пар V класу, має ступінь вільності W_гр, який дорівнює нулю. Розбити ці ланцюги на простіші кінема­тичні ланцюги, що мали б нульовий ступінь вільності, не­можливо.

Кінематичний ланцюг, який після приєднання його вільними елементами пар до інших ланок механізму не змінює його ступінь вільності і який не можна роз'єднати на простіші кінематичні ланцюги нульового ступеня вільності, називається структурною групою, або групою Ассура.

Таким чином, плоский механізм (див. рисунок 4.10, а) з одним ступенем вільності можна розглядати як такий, що утворений послідовним приєднанням до механізму І класу двох груп: групи 23 і групи 45. Тепер можна дати таке визначення основному принципу утворення механізмів.

Будь-який механізм можна одержати, якщо до механізму (механізмів) І класу послідовно приєднувати структурні групи.

При послідовному приєднанні груп необхідно керуватися певними правилами. При утворенні механізму з одним ступе­нем вільності перша група приєднується вільними елемента­ми ланок до початкової ланки і стояка. Наступні групи мо­жуть приєднуватися до будь-яких ланок одержаного ме­ханізму тільки так, щоб ланки групи могли рухатися відносно одна одної. Неможна групу вільними елементами приєднува­ти до одної ланки, оскільки у цьому випадку отримаємо неру­хомий контур.

Структурні групи плоских механізмів задовольняють умову

W_rp = 3n  2p₅  p₄ = 0,

структурні групи просторових механізмів 

W_rp = 6n  5р₅  4р₄  3p₃  2р₂  p₁ = 0.

Як плоскі, так й просторові структурні групи використову­ються не тільки при структурному синтезі, але й при аналізі ме­ханізмів.

4.4 Приклад структурного аналізу кривошипно-коромислового механізму (рисунок 4.11)

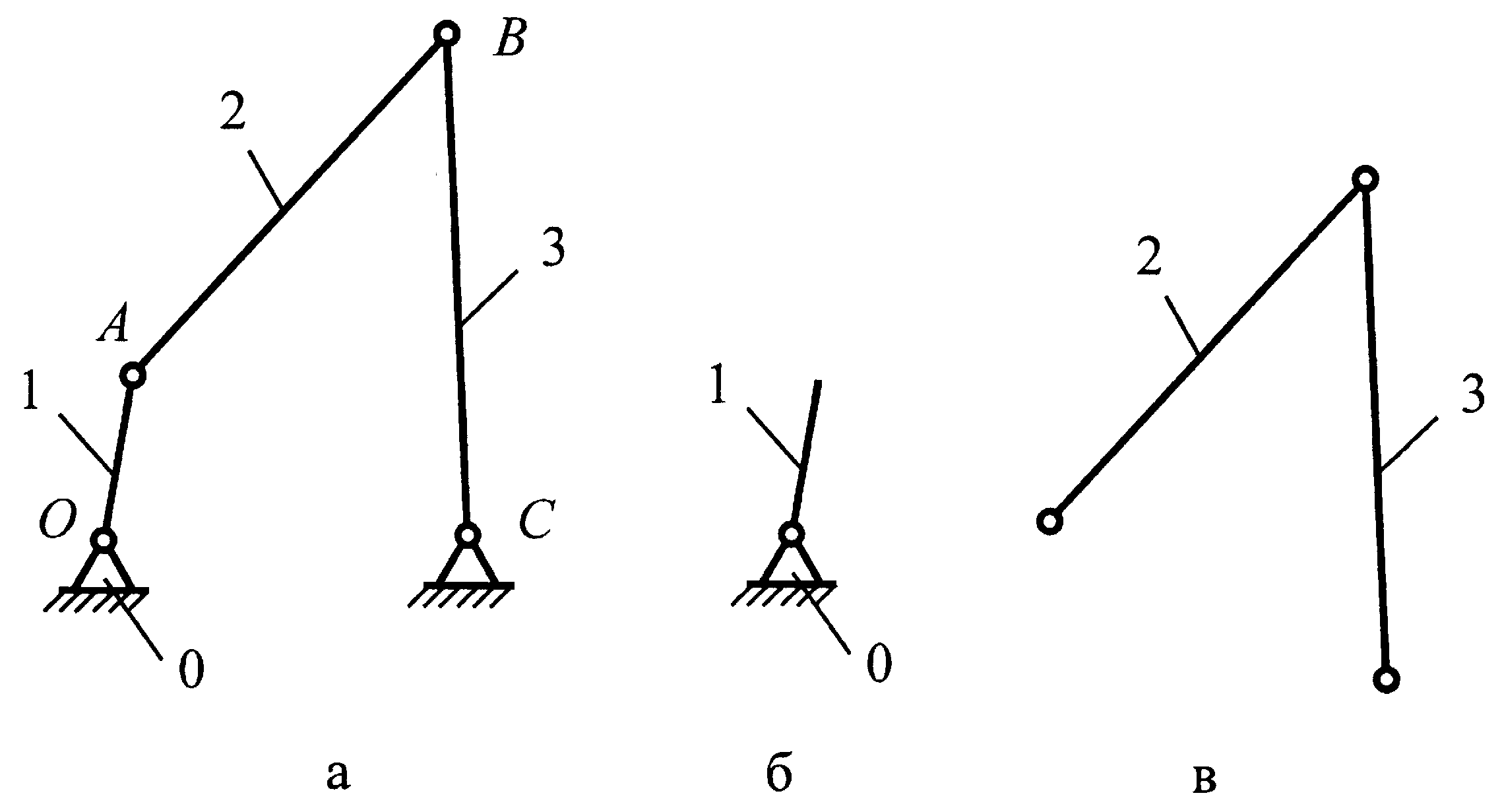
Рисунок 4.11 – Кривошипно-коромисловий механізм

1) Нумеруємо ланки. Стояк завжди нумерується цифрою 0, кривошип – 1. Далі нумерація проводиться в напрямі від механізму I класу до стояка.

Механізм складається зі стояка 0, кривошипа 1, шатуна 2, коромисла 3. Кількість рухомих ланок механізму n = 3.

2) Позначаємо кінематичні пари. Пара між стояком і кривошипом позначається великою літерою О. Наступні пари позначаються по порядку в напрямі від механізму I класу до стояка великими літерами латинського алфавіту: А, В, С, D, E, F, G, H, …

Кінематичні пари: 0-1, 1-2, 2-3, 3-0. Всі пари нижчі, плоскі, однорухомі, тобто 5-го класу. Їх кількість p₅ = 4; кінематичні пари 4-го класу відсутні, тобто p₄ = 0.

3) Визначаємо число ступенів рухомості плоского механізму за структурною формулою Чебишева:

W = 3n – 2p₅ – p₄ = 33 - 24 – 0 = 1.

4) Виділяємо механізм I класу (рисунок 4.11, б) та групу Ассура (рисунок 4.11, в).

5) Формула будови механізму:

I клас (0,1)  II клас (2,3).

Маємо механізм II класу.

ЛЕКЦІЯ 4 (продовження)