
- •6. Застосування рядів в числових розрахунках
- •6.1 Теоретичні відомості
- •6.1.1 Наближені обчислення значень функцій: теоретичні відомості
- •Подання функцій за допомогою рядів Тейлора (Маклорена): задачі для сомостійної роботи
- •6.1.2 Обчислення інтегралів: теоретичні відомості
- •6.1.3 Інтегрування диференціальних рівнянь: теоретичні відомості
- •6.1.4 Обчислення границь: теоретичні відомості
- •6.2 Наближені обчислення за допомогою рядів
- •6.2.1 Наближені обчислення значень функцій: приклади розв’язування завдань
- •6.2.1 Наближені обчислення значень функцій: завдання для самостійної та домашньої робіт
- •6.2.2 Обчислення інтегралів: приклади розв’язування завдань Вправи
- •6.2.2 Обчислення інтегралів: завдання для самостійної та домашньої робіт Вправи
- •3. Знайти з точністю до 0,001 координати центра маси дуги гіперболи між точками з абсцисами
- •Різні задачі
- •6.2.3 Інтегрування диференціальних рівнянь: приклади розв’язування завдань Приклади
- •6.2.3 Інтегрування диференціальних рівнянь: завдання для самостійної та домашньої робіт
- •6.2.4 Обчислення границь: приклади розв’язування завдань
- •6.2.4 Обчислення границь: завдання для самостійної та домашньої робіт
6. Застосування рядів в числових розрахунках
6.1 Теоретичні відомості
Тут ми зупинимося на деяких застосуваннях рядів Тейлора:

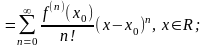 (5.1)
(5.1)
та Маклорена (одержується з (5.1)
при
 ):
):
 (5.1*)
(5.1*)
Розклади в ряд Маклорена деяких елементарних функцій мають вигляд:
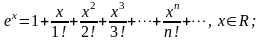 (5.2)
(5.2)
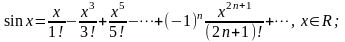 (5.3)
(5.3)
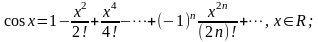 (5.4)
(5.4)
 (5.5)
(5.5)
 (5.6)
(5.6)
біноміальний ряд:
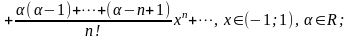 (5.7)
(5.7)
при
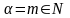 маємо (з попереднього ряду) біном Ньютона:
маємо (з попереднього ряду) біном Ньютона:
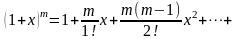
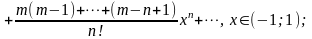 (5.7.1)
(5.7.1)
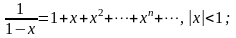 (5.7.2)
(5.7.2)
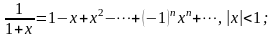 (5.7.3)
(5.7.3)
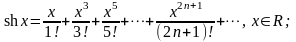 (5.8)
(5.8)
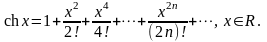 (5.9)
(5.9)
6.1.1 Наближені обчислення значень функцій: теоретичні відомості
Припустимо, що функцію
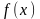 можна розкласти в степеневий ряд
(Тейлора) в інтервалі
можна розкласти в степеневий ряд
(Тейлора) в інтервалі
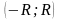 .
Тоді точне значення функції в довільній
точці
.
Тоді точне значення функції в довільній
точці
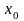 цього інтервалу визначається сумою
числового ряду, який утворюється із
степеневого ряду при
цього інтервалу визначається сумою
числового ряду, який утворюється із
степеневого ряду при
 ,
а наближене значення функції
в точці
дорівнює частинній сумі цього ряду
,
а наближене значення функції
в точці
дорівнює частинній сумі цього ряду
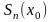 .
Похибку
.
Похибку
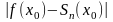 можна знайти, оцінюючи залишок
можна знайти, оцінюючи залишок
 ряду.
ряду.
Тобто для знаходження наближеного
значення функції
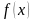 в її розкладі в степеневий ряд зберігають
перші
в її розкладі в степеневий ряд зберігають
перші
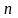 членів (
-
кінцева величина), а інші члени відкидають.
Для оцінки похибки знайденого наближеного
значення оцінюють суму відкинутих
членів.
членів (
-
кінцева величина), а інші члени відкидають.
Для оцінки похибки знайденого наближеного
значення оцінюють суму відкинутих
членів.
Якщо даний ряд знакосталий, то ряд, сформований з відкинутих членів, порівнюють з нескінченно спадною геометричною прогресією. У випадку знакозмінного ряду, члени якого задовольняють ознаку Лейбніца, використовується оцінка:
 ,
(5.10)
,
(5.10)
де
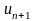 - перший з відкинутих членів ряду.
- перший з відкинутих членів ряду.
Обчислення значень тригонометричних
функцій. Щоб обчислити наближені
значення
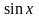 та
та
 ,
користуються відповідно рядами (5.3) та
(5.4). При будь-якому фіксованому значенні
,
користуються відповідно рядами (5.3) та
(5.4). При будь-якому фіксованому значенні
 ці ряди є знакозмінними рядами
лейбніцівського типу, тому для забезпечення
заданої точності обчислення користуються
нерівністю (5.10).
ці ряди є знакозмінними рядами
лейбніцівського типу, тому для забезпечення
заданої точності обчислення користуються
нерівністю (5.10).
Обчислення числа
 і його степеня, та числа
і його степеня, та числа
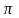 .
Якщо в ряд (5.2) підставити
.
Якщо в ряд (5.2) підставити
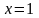 ,
то одержимо числовий ряд для наближеного
обчислення числа
:
,
то одержимо числовий ряд для наближеного
обчислення числа
:
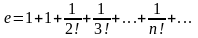 .
(5.11)
.
(5.11)
Виведемо формулу для оцінки похибки обчислень за рівністю (5.11). Для цього оцінимо -й залишок ряду (5.11):

(ряд в останніх дужках є геометричною
прогресією,
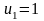 ,
,
 ).
Отже, якщо в ряді (5.11) взяти
перших членів, то похибка при цьому
визначається нерівністю
).
Отже, якщо в ряді (5.11) взяти
перших членів, то похибка при цьому
визначається нерівністю
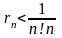 . (5.12)
. (5.12)
Для наближеного обчислення числа можна скористатися рядом (5.5):
при
 одержуємо
одержуємо

З останньої рівності:
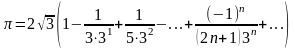 .
.
Цей ряд лейбніцівсього типу, тому для забезпечення заданої точності користуються нерівністю (5.10).
Для знаходження степеня числа використовують наближену рівність:
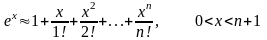 .
(5.13)
.
(5.13)
Похибка наближеної рівності (5.13)
визначається сумою членів, наступних
після
 в розкладі
в розкладі
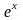 :
:

або
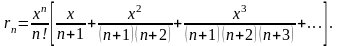
Замінивши кожен із множників
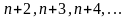 меншою величиною
меншою величиною
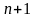 ,
одержимо нерівність.
,
одержимо нерівність.
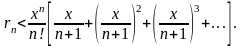
Знайдемо суму нескінченно спадної геометричної прогресії в квадратних дужках:
 (5.14)
(5.14)
Обчислення логарифмів. Розглянемо ряд (5.6):
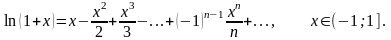
Коефіцієнти цього ряду спадають
досить повільно. Про такі ряди кажуть,
що вони збігаються повільно. Незручність
використання таких рядів пов’язана з
необхідністю обчислення великої
кількості членів ряду для забезпечення
заданої точності. Крім того, цей ряд
можна використовувати тільки для чисел
виду
 ,
які лежать в інтервалі
,
які лежать в інтервалі
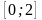 .
Тому виведемо більш зручну формулу для
обчислення логарифмів.
.
Тому виведемо більш зручну формулу для
обчислення логарифмів.
Підставивши в рівність (5.6) замість
число
 ,
матимемо
,
матимемо
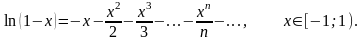 (5.15)
(5.15)
Віднімемо почленно з рівності(5.6) рівність (5.15):
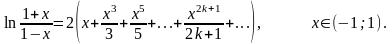
При
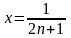 остання рівність набуває вигляду
остання рівність набуває вигляду
 (5.16)
(5.16)
Цією формулою користуються для обчислення
натуральних логарифмів при
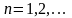 .
Десятковий логарифм пов’язаний з
натуральним рівністю
.
Десятковий логарифм пов’язаний з
натуральним рівністю
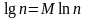 ,
де
,
де
 - модуль переходу. Тому для обчислення
десяткових логарифмів одержуємо формулу:
- модуль переходу. Тому для обчислення
десяткових логарифмів одержуємо формулу:
 (5.17)
(5.17)
Тому для обчислення логарифмів
можна використовувати наближену рівність
(одержується з (5.16) заміною
на
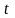 )
)
 .(5.18)
.(5.18)
Ряд правої частини рівності (5.18) збігається тим скоріше, чим більше .
Оцінимо похибку наближеної рівності (5.18) (для того, щоб цього не робити кожен раз при різних значеннях ).
Задача зводиться до оцінки суми залишку ряду (5.18):
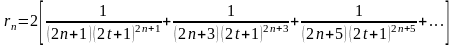 .
.
Замінивши кожен із множників
 меншим числом
меншим числом
 ,
одержимо нерівність:
,
одержимо нерівність:
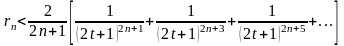 .
.
Знайдемо суму нескінченно спадної геометричної прогресії в квадратних дужках:

(5.19)
Обчислення коренів. Для наближеного обчислення коренів користуються біноміальним рядом (5.7):

При певних значеннях
 за допомогою цієї рівності наближено
добувають корені різного степеня із
заданого дійсного числа. Звернемо увагу
на те, що формула справедлива при
за допомогою цієї рівності наближено
добувають корені різного степеня із
заданого дійсного числа. Звернемо увагу
на те, що формула справедлива при
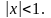 На перший погляд може здатися, що
використання цієї формули досить
обмежене, проте в кожному конкретному
випадку дійсне число подають у такому
вигляді, щоб можна було користуватися
рівністю (5.7).
На перший погляд може здатися, що
використання цієї формули досить
обмежене, проте в кожному конкретному
випадку дійсне число подають у такому
вигляді, щоб можна було користуватися
рівністю (5.7).
