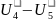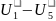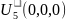Приложение а Методические рекомендации по проведению эксперимента идентификации пути поиска несоответствия продукции

РУКОВОДСТВО ПО ПРОВЕДЕНИЮ ЭКСПЕРИМЕНТА

АНКЕТА

Эксперимент состоит из трех этапов:

1. Выявление возможных влияющих факторов на качество продукции

2. Полнофакторный эксперимент по оценке значимости факторов на качество продукции;

3. Эксперимент по определению первоочередного пути поиска причины дефекта.

Этап 1

Для проведения эксперимента необходимо провести идентификацию потенциально влияющих факторов на качество продукции. Математическая зависимость выглядит следующим образом:

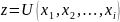
где – качество продукции;

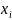– потенциально влияющий фактор;

Поскольку качество продукции зависит в первую очередь от качества процесса, который является преобразованием всех ресурсов, поступающих на вход, в выходы. В общем случае все ресурсы можно разделить на ресурс типа «Механизм», ресурс типа «Управление» и ресурс типа «Вход», которые являются комплексными и декомпозируются на составляющие, как показано на рисунке В.1.

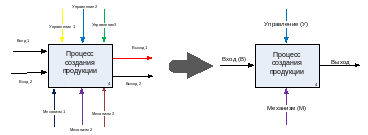
Рисунок В.1 – Идентификация влияющих факторов и их комплексирование

К каждому ресурсу предъявляется комплекс требований, по которым определяется его соответствие или несоответствие. При проведении эксперимента рассматриваются две крайние ситуации:

0 – ресурс, не соответствующий требованиям;

1 – ресурс, соответствующий требованиям.

Этап 2

Цели:

- оценка влияния факторов «Механизм», «Управление», «Вход» на качество продукции;

- оценка независимости (взаимного влияния) факторов.

Для оценки значимости каждого фактора на качество ресивера необходимо провести ПФЭ методом попарного альтернативного сопоставления. Для оценивания применяется шкала сравнительного превосходства, представлення в таблице В.1

Таблица В.1 – Шкала сравнительного превосходства

Ранг	Определение	Балл
A	Одинаковый уровень значимости	0
B	Почти эквивалентный уровень значимости	1
C	Несколько предпочтительней уровень значимости	3
D	Значительно предпочтительней уровень значимости	5
E	Строго предпочтительней уровень значимости	7
F	Строго предпочтительней уровень значимости	8
2,4,6	Промежуточные значения между двумя соседними рангами

Для построения модели эксперимента используется метод покоординатного спуска, так как точек эксперимента восемь, а метод оценивания – попарное альтернативное сопоставление. Получается 3 итерации проведения эксперимента, как показано на рисунке В.2 и таблице В.1.

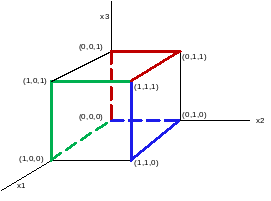
Рисунок В.2 – Метод покоординатного спуска

Таблица В.1 – Схема проведения эксперимента по итерациям

Итерация 1	Итерация 2	Итерация 3

Далее по каждой итерации проводится оценивание с привлечением эксперта методом попарного альтернативного сопоставления (таблицы В.2-В.4)

Таблица В.2 - Итерация 1

План A1		План B1
Принимаем

Таблица В.3 – Итерация 2

План A2		План B2
Принимается

Таблица В.3 – Итерация 3

План A3			План B3
Принимается

Нормализованные данные по всем итерациям представляются в общую таблицу В.5

Таблица В.5 – Нормализованные данные

План А		План В
	1			1
	0			0

Обработав данные эксперимента, необходимо проверить устойчивость результатов экспертного эксперимента по критерию К₁.

Критерий К₁: Считаем, что результаты экспертного оценивания устойчивы, если данные связаны линейной возрастающей значимой зависимостью, т.е. справедлива следующая зависимость:

где – результат эксперимента по плану А и по плану В соответственно;

– линейный коэффициент;

– свободный коэффициент.

Выдвигается гипотеза H₀, которая сформулирована следующим образом: коэффициент линейного уравнения равен 0: .

Если вероятность p<0,2, то гипотеза отвергается.

Задачу линейной линейной регрессии решаем с помощью пакета Statistica.

Полнофакторный эксперимент предполагает следующую математическую модель:

,

где – линейные эффекты (коэффициенты);

– эффекты (коэффициенты) парного взаимодействия;

– эффект (коэффициенты) тройного взаимодействия.

Необходима проверить модель эксперимента на значимость. Для этого принимаем гипотезу H₀, которая звучит следующим образом: коэффициент линейных, парных или тройных взаимодействий равны нулю. Для проверки гипотезы необходимо определить уровень значимости p-level: p=0,05. Если p>0,05 – гипотеза принимается. Если p<0,05 – гипотеза отвергается.

Гипотеза H₀ проверяеется с помощью пакета Statistica.

После получения уравнения линейной регрессии делается вывод о значимости факторов «Механизм», «Управление», «Вход» на качество продукции и проводится третий этап по определению первоочередного пути поиска несоответствия продукции.

Этап 3

Цели:

- оценка вероятности того, что причиной появления дефекта является тот или иной фактор;

- определение первоочередного пути поиска причины дефекта.

Три выделенных фактора:

– ресурс типа «Механизм»;

– ресурс типа «Управление»;

– ресурс типа «Вход»

оказывают влияние на качество ресивера. На данном этапе эксперимента необходимо оценить вероятность того, что причиной дефекта ресивера будет ресурс типа «Механизм», ресурс типа «Управление», ресурс типа «Вход». Это необходимо для того, чтобы определить первоочередной путь поиска причины при возникновении дефекта.

Для определения вероятностей применим методом попарного альтернативного сопоставления. Для оценивания применяется шкала сравнительного превосходства, представленная в таблице В.6

Таблица В.6 – Шкала сравнительного превосходства

Ранг	Определение	Балл
A	Одинаковый уровень значимости	0
B	Почти эквивалентный уровень значимости	1
C	Несколько предпочтительней уровень значимости	3
D	Значительно предпочтительней уровень значимости	5
E	Строго предпочтительней уровень значимости	7
F	Строго предпочтительней уровень значимости	8
2,4,6	Промежуточные значения между двумя соседними рангами

Рассматриваются две крайние ситуации, когда все факторы принимают наихудшие и наилучшие значения, и промежуточные ситуации, когда один из факторов принимает наихудшее значение (0), а остальные – максимальные значения (1).

Рассматриваются одна крайняя ситуации, когда все факторы принимают наилучшие значения, и промежуточные ситуации, когда один из факторов принимает наихудшее значение (0), а остальные – максимальные значения (1). Возможны ситуации представлены в таблице В.7:

Таблица В.7 – Возможные ситуации

Математическое выражение ситуации	Пояснение
	Причина дефекта – ресурс «Механизм» при условии, что ресурсы «Управление» и «Вход» соответствуют требованиям
	Причина дефекта – ресурс «Управление» при условии, что ресурсы «Механизм» и «Вход» соответствуют требованиям
	Причина дефекта – ресурс «Вход» при условии, что ресурсы «Механизм» и «Управление» соответствуют требованиям
	Ситуация при условии, ресурсы «Механизм», «Управление» и «Вход» соответствуют требованиям

Далее следует оценивание с привлечением эксперта методом попарного альтернативного сопоставления (Таблица В.8)

Таблица В.8 – Результаты экспертного оценивания

План A		План B
					-
					-
					-
					-
U5		U5			-
U4		U4			-
U3		U3			-
U2		U2			-
U1		U1			-
Принимаем

Обработав данные эксперимента, необходимо проверить устойчивость результатов экспертного эксперимента по критерию К₁.

Критерий К₁: Считаем, что результаты экспертного оценивания устойчивы, если данные связаны линейной возрастающей значимой зависимостью, т.е. справедлива следующая зависимость:

где – результат эксперимента по плану А и по плану В соответственно;

– линейный коэффициент;

– свободный коэффициент.

Выдвигается гипотеза H₀, которая сформулирована следующим образом: коэффициент линейного уравнения равен 0: .

Если вероятность p<0,2, то гипотеза отвергается.

Задачу линейной линейной регрессии решаем с помощью пакета Statistica.

После получения нормализованных данных экспертного оценивания делается заключение о первоочередном пути поиска несоответствия, т.е. определяется фактор «Механизм», «Управление» или «Вход», который имеет наибольшую вероятность быть причиной дефекта.

Для дальнейшего определения пути поиска причины дефекта необходимо повторить эксперимент при влиянии факторов определенного ресурса более низкого уровня декомпозиции, поскольку каждый ресурс процесса является результатом деятельности (выходом) другого процесса, который, в свою очередь имеет свои ресурсы на входе.