Питання для самоперевірки знань, умінь

1. Визначники другого та третього порядків.

2. Правило трикутників для обчислення визначників.

3. Розклад визначника за елементами рядка (стовпця.)

4. Правило Саррюса.

5. Що таке прямокутна матриця? Елементи матриці. Стовпці і рядки матриці.

6. Яка матриця називається квадратною? Головна діагональ матриці. Бічна діагональ матриці

7. Що таке сума матриць?Що таке добуток матриці на число?

8. Що таке добуток двох матриць?

Висновок _________________________________________________________

____________________________________________________________________________________________________________________________________

Перевірив викладач ___________ Оцінка ___________ Дата ______________

Виконаємо самостійно

В-1 В-2

1) Обчислити визначники, використовуючи:

а)правило трикутників;

б) метод розкладу за елементами першого рядка;

в) правило Саррюса

2) Знайти , якщо

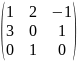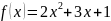А= , А= ,

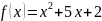
3) Знайти матрицю , , якщо

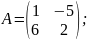
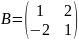
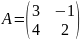
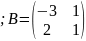
В-3 В-4

1. Обчислити визначники, використовуючи:

1. правило трикутників;

б) метод розкладу за елементами першого рядка;

в) правило Саррюса

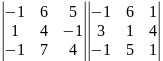
2) Знайти , якщо

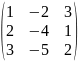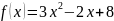А= , А= ,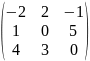

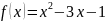
3) Знайти матрицю 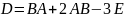, , якщо

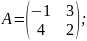
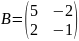
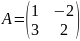
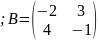
Практична робота № 2 Тема. Розв’язування систем лінійних рівнянь основними методами: методом Гауса, за формулами Крамера

Мета роботи: навчитись розв’язувати системи лінійних рівнянь методами Крамера та Гауса.

Наочне забезпечення та обладнання:

1. Інструкційні картки;

2. Індивідуальні завдання;

3. Обчислювальні засоби.

Теоретичні відомості про правило Крамера

Розглянемо систему n лінійних рівнянь з n невідомими:

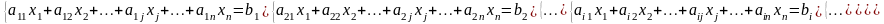(1.4)

Теорема. Якщо головний визначник 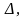складений із коефі­цієнтів при невідомих системи n лінійних рівнянь з n невідомими (1.4), відмінний від нуля, то така система рівнянь має єдиний розв’язок (сумісна і визначена), який обчислюється за формулами:

,

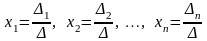де 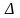— головний визначник системи, який утворюється з коефіцієнтів при невідомих у лівій частині системи (1.4);

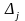— визначник, який утворюється заміною j-го стовпця в головному визначнику на стовпець вільних членів.

Задача 1. Розв’язати систему лінійних рівнянь за правилом Крамера:

a)

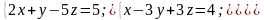
Теоретичні відомості про Метод Гауса розв’язування систем лінійних рівнянь

Метод Гауса називають ще методом послідовного виключення невідомих. Він полягає в наступному: систему рівнянь приводять до рівносильної їй системі з трикутною матрицею ( системи називаються рівносильними, якщо множини їх розв’язків співпадають). Дані дії називаються прямим ходом. З одержаної системи невідомі знаходять за допомогою послідовних підстановок, які називають зворотнім ходом. При виконанні прямого ходу використовують наступні перетворення:

1. множення або ділення коефіцієнтів вільних членів на одне і теж число;

2. додавання або віднімання рівнянь;

3. перестановка рівнянь системи;

4. виключення з системи рівнянь, в яких всі коефіцієнти при невідомих дорівнюють нулю.

Універсальність методу Гауса полягає в тому, що за допомогою нього можна розв’язати систему будь-якого порядку. Продемонструємо розв’язування системи лінійних рівнянь методом Гауса на загальному прикладі.

Розв’яжемо систему лінійних рівнянь:

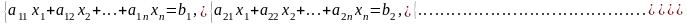(1)

Систему лінійних рівнянь (1) можна записати у вигляді розширеної матриці:

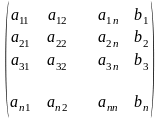(2)

1) Прямий хід: розширену матрицю (2) шляхом послідовного виконання лінійних операцій над її рядками ( тобто послідовного виконання операції додавання до одного рядка матриці іншого, помноженого на певне число) приводять до вигляду:

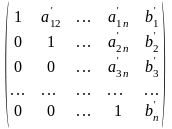(3)

2) Зворотній хід: від розширеної матриці (3) переходять до відповідної системи рівнянь:

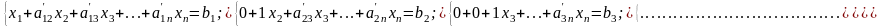(4)

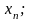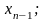Останнє рівняння системи (4) дає значення змінної підставляючи це значення в передостаннє рівняння знаходимо змінну продовжуючи цей процес, поступово знаходимо значення всіх невідомих.

Задача 2. Розв’язати систему лінійних рівнянь методом Гауса:

a)