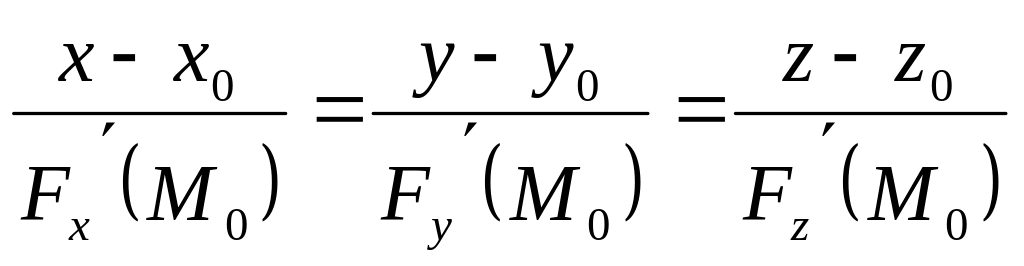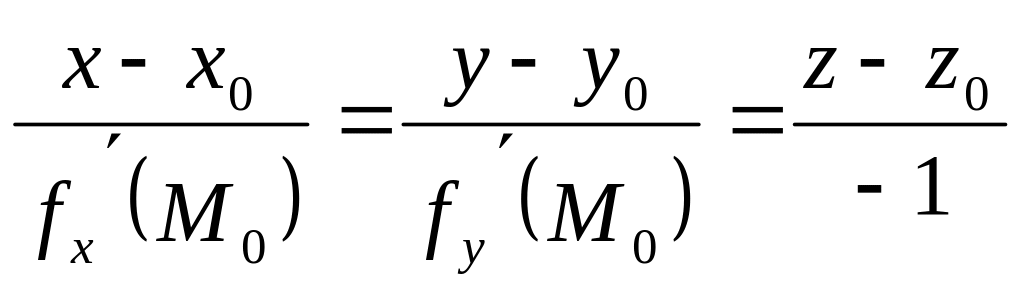7. Знайти довжину вектора якщо :
А |
Б |
В |
Г |
|
|
|
|
8. Умова паралельності двох прямих на площині має вигляд:
А |
Б |
В |
Г |
|
|
|
|
9. Відстань від точки до площини у просторі знаходиться за формулою:
А |
Б |
В |
Г |
|
|
|
|
10. Написати рівняння прямої, що проходить через точку паралельно до прямої :
А |
Б |
В |
Г |
|
|
|
|
11. Знайти границю
А |
Б |
В |
Г |
0 |
1 |
2 |
3 |
12. Знайти похідну функції
А |
Б |
В |
Г |
|
|
|
|
13. Частинною похідною функції z=f(x,y) по змінній y називається:
А |
Б |
В |
Г |
|
|
|
|
14. Знайти частинну похідну функції
,якщо
А |
Б |
В |
Г |
|
|
|
|
15. Записати формулу таблиці інтегралів
А |
Б |
В |
Г |
|
|
|
|
16. Якщо всюди на відрізку [a,b]
функція
то виконується нерівність
А
|
Б |
В |
Г |
|
|
|
|
17. Обчисліть невизначений інтеграл
А |
Б |
В |
Г |
|
2 |
|
|
18. Записати формулу таблиці інтегралів
А |
Б |
В |
Г |
|
|
|
|
19. Однорідні рівняння зводяться до рівнянь з відокремлюваними змінними за допомогою підстановки:
А |
Б |
В |
Г |
|
|
|
|
20. Рівнянням Бернуллі називається рівняння виду:
А |
Б |
В |
Г |
|
|
|
|
Комплексна контрольна робота
з вищої математики
для студентів групи Ф-300
варіант 16
1. Нехай задано систему двох лінійних
рівнянь, з двома невідомими
тоді:
А |
Б |
В |
Г |
|
|
|
|
2. Розв’язок системи рівнянь у матричній формі можливий лише тоді, коли матриця системи:
А |
Б |
В |
Г |
Невироджена |
Вироджена |
Діагональна |
Узгоджена |
3. Обчислити визначник третього порядку :
А |
Б |
В |
Г |
0 |
-2 |
1 |
2 |
4. знайти А+2В-Е якщо і :
А |
Б |
В |
Г |
|
|
|
|
5. Орт вектора знаходиться за формулою:
А |
Б |
В |
Г |
|
|
|
|
6. Скалярний добуток двох ненульових векторів дорівнює нулю тоді і тільки тоді, коли вектори:
А |
Б |
В |
Г |
Паралельні |
Компланарні |
Перпендикулярні |
Колінеарні |
7. Кут між векторами
і
,довжини
векторів
Обчислити
:
А |
Б |
В |
Г |
25 |
12 |
1 |
13 |
8. Множина всіх точок площини, сума відстаней яких від двох даних точок цієї площини, які називаються фокусами, є величина стала називається:
А |
Б |
В |
Г |
Еліпсом |
Колом |
Гіперболою |
Параболою |
9. Канонічне рівняння параболи вітки якої направлені вверх має вигляд:
А |
Б |
В |
Г |
|
|
|
|
10. Написати рівняння площини, що проходить через точку перпендикулярно до вектора :
А |
Б |
В |
Г |
|
|
|
|
11. Знайти границю
А |
Б |
В |
Г |
0 |
1 |
2 |
3 |
12. Знайти похідну функції
А |
Б |
В |
Г |
|
|
|
|
13. Якщо поверхню задано рівнянням
F(x,y,z)=0
то рівняння дотичної площини в точці
має вигляд:
А |
Б |
|
|
B |
Г |
|
|
14. Знайти частинну похідну функції
,якщо
А |
Б |
В |
Г |
|
|
|
|
15. Записати формулу таблиці інтегралів
А |
Б |
В |
Г |
|
|
|
|
16. Якщо функція f(x) інтегрована на відрізку [а,b] то
А |
Б |
В |
Г |
|
|
|
|
17. Обчисліть невизначений інтеграл
А |
Б |
В |
Г |
|
|
|
|
18. Записати формулу таблиці інтегралів
А |
Б |
В |
Г |
|
|
|
|
19. Рівняння вигляду
,
яке не містить незалежної змінної х,
розв’язується за допомогою підстановки:
А |
Б |
В |
Г |
|
|
|
|
20. Графік розв’язку диференціального рівняння називається:
А |
Б |
В |
Г |
Диференціальною кривою |
Інтегральною кривою |
Кривою розв’язку |
Геометричною кривою |
Комплексна контрольна робота
з вищої математики
для студентів групи Ф-300
варіант 17
1. Діагональна матриця, у якої кожен елемент головної діагоналі дорівнює одиниці, називається:
А |
Б |
В |
Г |
Квадратною |
Симетричною |
Нульовою |
Одиничною |
2. Матриця називається оберненою до матриці А, якщо виконується умова:
А |
Б |
В |
Г |
|
|
|
|
